Rotationsträgheit
Quelle: Nicholas Timmons, Asantha Cooray, PhD, Department of Physics & Astronomie, School of Physical Sciences, University of California, Irvine, CA
Trägheit ist der Widerstand eines Objekts wird beschleunigt. In lineare Kinematik bezieht sich dieses Konzept direkt auf die Masse des Objekts. Die massivere ein Objekt, desto mehr Kraft ist erforderlich, um das Objekt zu beschleunigen. Dies sieht man direkt in Newtons zweites Gesetz, die besagt, dass Kraft gleich Masse mal Beschleunigung.
Für die Rotation gibt es ein ähnliches Konzept Rotationsträgheit genannt. In diesem Fall ist Rotationsträgheit der Widerstand eines Objekts wird rotatorisch beschleunigt. Rotationsträgheit ist nicht nur abhängig von Masse, sondern auch auf den Abstand der Masse vom Zentrum der Rotation.
Das Ziel dieses Experiments ist die Rotationsträgheit zwei rotierenden Massen zu messen und die Abhängigkeit von Masse und Entfernung von der Drehachse bestimmen.
Einem bestimmten Objekt oder System von Objekten hat einige Rotationsträgheit. Die Rotationsträgheit um eine bestimmte Achse nennt man das Trägheitsmoment. Da der Abstand zwischen der Masse der Drehachse wichtig ist, kann ein einzelnes Objekt haben sehr unterschiedliche Trägheitsmomente, die abhängig von der Achse, über die es sich dreht. Das Trägheitsmoment für ein Objekt ist wie folgt definiert:
 , (Gleichung 1)
, (Gleichung 1)
wo i ist die Anzahl der Objekte.
In Gleichung 1ist r der Abstand zwischen der Drehachse der Masse. Wie in der Gleichung ersichtlich ist das Trägheitsmoment abhängig von der Masse des Objekts und dem Quadrat der Entfernung aus der Masse um die Drehachse.
Nur wie wie lineare Kinematik Bewegungsgleichungen hat, hat Rotations Kinematik analoge Bewegungsgleichungen. Zum Beispiel ist Newtons zweite Gesetz für lineare Bewegung:
 . (Gleichung 2)
. (Gleichung 2)
Eine ähnliche Rotations Gleichung hat die Form:
 , (Gleichung 3)
, (Gleichung 3)
wo 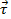 wird das Drehmoment
wird das Drehmoment 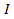 ist das Trägheitsmoment und
ist das Trägheitsmoment und  ist die Winkelbeschleunigung. Hier ist das Trägheitsmoment der analogen des Begriffs Masse in Newtons zweites Gesetz. Ebenso ist das Trägheitsmoment in anderen wichtigen Gleichungen der Drehbewegung:
ist die Winkelbeschleunigung. Hier ist das Trägheitsmoment der analogen des Begriffs Masse in Newtons zweites Gesetz. Ebenso ist das Trägheitsmoment in anderen wichtigen Gleichungen der Drehbewegung:
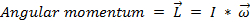 , (Gleichung 4)
, (Gleichung 4)
 , (Gleichung 5)
, (Gleichung 5)
wo 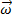 ist die Winkelgeschwindigkeit des Objekts.
ist die Winkelgeschwindigkeit des Objekts.
Für dieses Experiment ist eine Masse mit einem rotierenden Arm mit einer Schnur umwickelt die Drehachse verbunden. Siehe Abbildung 1 für ein Bild vom Aussehen der Versuchsaufbau. Zwei Massen zu den rotierenden Arm verbunden werden, Reibung wird in diesem Experiment ignoriert und das gesamte Trägheitsmoment wird gleich dem Moment der rotierenden Massen plus Moment des drehenden Arm sein.
Die Masse, die durch den Einfluss der Schwerkraft fällt, wird ein Drehmoment auf den rotierenden Arm erlassen. Aus Gleichung 2  und
und 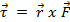 . Hier,
. Hier, 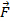 ist die Kraft auf das Objekt, das von der Spannung kommt
ist die Kraft auf das Objekt, das von der Spannung kommt 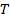 in der Zeichenfolge, und
in der Zeichenfolge, und  ist der Abstand von der Kraft um die Drehachse. Hier ist die Entfernung der Abstand vom Rand der Wunde Zeichenfolge um die Drehachse.
ist der Abstand von der Kraft um die Drehachse. Hier ist die Entfernung der Abstand vom Rand der Wunde Zeichenfolge um die Drehachse.
Die Winkelbeschleunigung  zeichnet sich durch
zeichnet sich durch  , wo
, wo  ist die lineare Beschleunigung eines Punktes auf der Wunde-Zeichenfolge, die die Beschleunigung der das Fallgewicht entspricht. Setzen alles zusammen gibt
ist die lineare Beschleunigung eines Punktes auf der Wunde-Zeichenfolge, die die Beschleunigung der das Fallgewicht entspricht. Setzen alles zusammen gibt 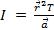 . Newtons zweite Gesetz wird verwendet, um die Spannung zu finden. Die Summe der Kräfte auf das Objekt sollte gleich der Masse mal Beschleunigung. Hier sind die Kräfte auf das Fallgewicht Schwerkraft (
. Newtons zweite Gesetz wird verwendet, um die Spannung zu finden. Die Summe der Kräfte auf das Objekt sollte gleich der Masse mal Beschleunigung. Hier sind die Kräfte auf das Fallgewicht Schwerkraft (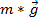 ) und die Spannung
) und die Spannung 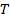 , so
, so 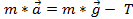 . Unter der Annahme einer konstanten Beschleunigung, dann
. Unter der Annahme einer konstanten Beschleunigung, dann 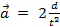 , wo
, wo  ist die Entfernung, die das Gewicht reist und
ist die Entfernung, die das Gewicht reist und  ist die Zeit, die es braucht, um diese Distanz zu fallen. Dies rührt die kinematischen Bewegungsgleichungen.
ist die Zeit, die es braucht, um diese Distanz zu fallen. Dies rührt die kinematischen Bewegungsgleichungen.
Setzen alles zusammen ergibt sich eine Formel für das Trägheitsmoment in Bezug auf die Mengen, die während des Tests messbar sind:
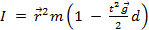 . (Gleichung 7)
. (Gleichung 7)
Wenn zwei Massen am drehenden Arm in gleichmäßigen Abständen angebracht sind ![]() von der Drehachse, dann wird das Trägheitsmoment sein:
von der Drehachse, dann wird das Trägheitsmoment sein:
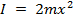 , (Gleichung 8)
, (Gleichung 8)
Das ist der theoretische Wert für dieses Experiment.

Abbildung 1. Versuchsaufbau.
1. Messen Sie das Trägheitsmoment der langen Stange.
- Wickeln Sie die Schnur befestigt, das Gewicht, bis das Gewicht in der Nähe der drehenden Arm ist.
- Legen Sie das Gewicht und Messen Sie die Zeit, die es braucht, um fallen als auch die Distanz, die er fällt.
- Führen Sie Schritt 1.2 dreimal und berechnen Sie die durchschnittliche Trägheitsmoment mit Gleichung 7.
- Die theoretische Trägheitsmoment der Spinnrute mit folgender Formel zu berechnen:
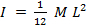 , wo
, wo  ist die Masse des Stabes und
ist die Masse des Stabes und 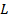 ist die Länge.
ist die Länge. - Vergleichen Sie den theoretischen Wert mit dem gemessenen Wert und notieren Sie den Unterschied.
(2) zwei Massen an der Rute befestigt.
- Platzieren Sie zwei 100-kg-Masse 20 cm weg von der Mitte des Stabes.
- Wiederholen Sie die Schritte 1.2 und 1.3 mit den beigefügten Massen.
- Das gesamte Trägheitsmoment sollte die Moment of inertia der angeschlossenen Massen sowie das Trägheitsmoment des Stabes entsprechen. Verwenden Sie diese Tatsache, die Ergebnisse aus Schritt 1 und Gleichung 8 um die theoretischen und experimentellen Trägheitsmomente für die angeschlossenen Massen bestimmen.
- Vergleichen Sie die theoretischen Werte mit den gemessenen Werten und notieren Sie die Unterschiede.
3. Wirkung der Abstand auf Trägheitsmoment.
- Wiederholen Sie Schritt 2 des Labors, aber 10 cm weg von der Drehpunkt der angehängten Masse nach. Beachten Sie die Änderungen in das Herabfallen von das Gewicht oder das Spinnen des Stabes.
- Vergleichen Sie die theoretischen Werte mit den gemessenen Werten und notieren Sie die Unterschiede.
4. Wirkung der Masse auf das Trägheitsmoment.
- Wiederholen Sie Schritt 2 des Labors, aber ändern Sie die Masse Größe bis 200 kg.
- Vergleichen Sie die theoretischen Werte mit den gemessenen Werten und notieren Sie die Unterschiede.
| Theoretischer Wert
(kg m2) |
Experimentellen Wert
(kg m2) |
Unterschied
(%) |
|
| Teil 1 | 0,20 | 0,22 | 10 |
| Teil 2 | 0,08 | 0,07 | 14 |
| Teil 3 | 0.02 | 0.02 | 0 |
| Teil 4 | 0,16 | 0,15 | 6 |
Die Ergebnisse des Experiments bestätigen die Prognosen von Gleichungen 7 und 8. Das Trägheitsmoment für eine Spinnrute, wie Sie durch die Formel in Schritt 1.4, wurde experimentell bestätigt. Der verringerte Abstand in Schritt 3 führte ein kleiner Trägheitsmoment, wie vorhergesagt. Die größere Masse in Schritt 4 ergab ein größeres Trägheitsmoment, wie vorhergesagt durch Gleichung 8.
Haben Sie sich jemals gefragt, warum ein Seiltänzer einen sehr langen Stab trägt? Der Grund ist, dass die langen Stab eine sehr große Trägheitsmoment aufgrund seiner Länge hat. Daher erfordert es eine große Menge an Drehmoment zu drehen. Dies hilft der Seiltänzer, ausgewogen, bleiben, wie die Pole stabil bleiben wird.
Räder des Autos und Fahrräder sind nie nur solide Platten; Stattdessen haben sie Speichen, die das Rad von der Achse zu unterstützen. Dies ermöglicht ein leichteres Design welche Hilfsmittel mit Geschwindigkeit, aber der wahre Grund für dieses Design sein kann, erklärt Rotationsträgheit. Eine solide Scheibe hat ein größeres Trägheitsmoment als eine Reifen-ähnliche Form. Mit seinen kleineren Trägheitsmoment ein Reifen erfordert weniger Drehmoment zu drehen und vielleicht noch wichtiger ist, erfordert weniger Drehmoment ausgesetzt.
Wenn ein Baseball-Spieler auf bat gegen einen Krug Fastballs zu werfen ist, kann er seine Schaukel beschleunigen, um ein Hit zu bekommen wollen. Er kann dies erreichen, indem einfach bewegte seine Hände näher an das schwere Ende der Fledermaus, die heißt "Würgen sich." Dies verringert den Abstand von der Mitte der Masse des Bat um die Drehachse und erleichtert somit den Teig um die Fledermaus zu drehen.
In diesem Experiment wurden das Trägheitsmoment für einen Stab und zwei Massen experimentell gemessen und theoretisch berechnet. Die Unterschiede zwischen diesen Werten wurden untersucht. Die Wirkung der Masse auf das Trägheitsmoment wurde getestet, sowie die Wirkung der Abstand von der Drehachse.
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Rotationsträgheit
Physics I
43.5K Ansichten

Newtonsche Gesetze der Bewegung
Physics I
75.7K Ansichten

Kraft und Beschleunigung
Physics I
79.1K Ansichten

Vektoren in mehrere Richtungen
Physics I
182.3K Ansichten

Kinematik und Projektilbewegung
Physics I
72.6K Ansichten

Newtonsches Gravitationsgesetz
Physics I
190.8K Ansichten

Der Impulserhaltung
Physics I
43.3K Ansichten

Reibung
Physics I
52.9K Ansichten

Hookesches Gesetz und harmonische Schwingungen
Physics I
61.3K Ansichten

Gleichgewichts- und Freikörper-Diagramme
Physics I
37.3K Ansichten

Drehmoment
Physics I
24.3K Ansichten

Drehimpuls
Physics I
36.2K Ansichten

Energie und Arbeit
Physics I
49.7K Ansichten

Enthalpie
Physics I
60.4K Ansichten

Entropie
Physics I
17.6K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten