Momento di inerzia
Panoramica
Fonte: Nicholas Timmons, Asantha Cooray, PhD, Dipartimento di Fisica e Astronomia, Scuola di Scienze Fisiche, Università della California, Irvine, CA
L'inerzia è la resistenza di un oggetto ad essere accelerato. Nella cinematica lineare, questo concetto è direttamente correlato alla massa di un oggetto. Più un oggetto è massiccio, maggiore è la forza necessaria per accelerare quell'oggetto. Questo è visto direttamente nella seconda legge di Newton, che afferma che la forza è uguale all'accelerazione di massa.
Per la rotazione, esiste un concetto simile chiamato inerzia rotazionale. In questo caso, l'inerzia rotazionale è la resistenza di un oggetto ad essere accelerato rotazionalmente. L'inerzia rotazionale dipende non solo dalla massa, ma anche dalla distanza di massa dal centro di rotazione.
L'obiettivo di questo esperimento è misurare l'inerzia rotazionale di due masse rotanti e determinare la dipendenza dalla massa e dalla distanza dall'asse di rotazione.
Principi
Un certo oggetto o sistema di oggetti ha una certa inerzia rotazionale. L'inerzia rotazionale attorno a un certo asse è chiamata momento di inerzia. Poiché la distanza dalla massa all'asse di rotazione è importante, un singolo oggetto può avere momenti di inerzia molto diversi a seconda dell'asse attorno al quale ruota. Il momento di inerzia per un oggetto è definito come:
 , (Equazione 1)
, (Equazione 1)
dove i è il numero di oggetti.
Nell'equazione 1, r è la distanza dall'asse di rotazione alla massa. Come si può vedere nell'equazione, il momento di inerzia dipende dalla massa dell'oggetto e dal quadrato della distanza dalla massa all'asse di rotazione.
Proprio come la cinematica lineare ha equazioni del moto, la cinematica rotazionale ha equazioni analoghe del moto. Ad esempio, la seconda legge di Newton per il moto lineare è:
 . (Equazione 2)
. (Equazione 2)
Un'equazione rotazionale simile assume la forma:
 , (Equazione 3)
, (Equazione 3)
dove 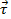 è la coppia, è il momento di
è la coppia, è il momento di 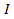 inerzia e è
inerzia e è  l'accelerazione angolare. Qui, il momento di inerzia è l'analogo del termine di massa nella seconda legge di Newton. Allo stesso modo, il momento di inerzia è presente nelle altre importanti equazioni del moto rottivo:
l'accelerazione angolare. Qui, il momento di inerzia è l'analogo del termine di massa nella seconda legge di Newton. Allo stesso modo, il momento di inerzia è presente nelle altre importanti equazioni del moto rottivo:
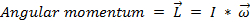 , (Equazione 4)
, (Equazione 4)
 , (Equazione 5)
, (Equazione 5)
dove 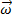 è la velocità angolare dell'oggetto.
è la velocità angolare dell'oggetto.
Per questo esperimento, una massa è collegata a un braccio rotante da una stringa avvolta attorno all'asse di rotazione. Vedere la Figura 1 per un'immagine dell'aspetto della configurazione sperimentale. Due masse saranno collegate al braccio rotante, l'attrito sarà ignorato in questo esperimento e il momento totale di inerzia sarà uguale al momento delle masse rotanti più il momento del braccio rotante.
La massa, che cade a causa dell'influenza della gravità, metterà in atto una coppia sul braccio rotante. Dall'equazione 2  e
e 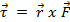 . Qui,
. Qui, 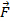 è la forza sull'oggetto, che proviene dalla tensione nella
è la forza sull'oggetto, che proviene dalla tensione nella 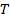 corda, ed è la
corda, ed è la  distanza dalla forza all'asse di rotazione. Qui, quella distanza è la distanza dal bordo della corda avvolta all'asse di rotazione.
distanza dalla forza all'asse di rotazione. Qui, quella distanza è la distanza dal bordo della corda avvolta all'asse di rotazione.
L'accelerazione angolare  è definita da
è definita da  , dove
, dove  è l'accelerazione lineare di un punto sulla corda avvolta che corrisponde all'accelerazione del peso in caduta. Mettere tutto insieme dà
è l'accelerazione lineare di un punto sulla corda avvolta che corrisponde all'accelerazione del peso in caduta. Mettere tutto insieme dà 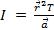 . La seconda legge di Newton è usata per trovare la tensione. La somma delle forze sull'oggetto dovrebbe essere uguale alla massa volte l'accelerazione. Qui, le forze sul peso che cade sono la gravità (
. La seconda legge di Newton è usata per trovare la tensione. La somma delle forze sull'oggetto dovrebbe essere uguale alla massa volte l'accelerazione. Qui, le forze sul peso che cade sono la gravità ( 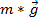 ) e la tensione , quindi
) e la tensione , quindi 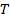
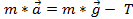 . Assumendo un'accelerazione costante, allora
. Assumendo un'accelerazione costante, allora 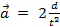 , dove è la
, dove è la  distanza percorsa dal peso e
distanza percorsa dal peso e  è il tempo necessario per cadere quella distanza. Questo deriva dalle equazioni cinematiche del moto.
è il tempo necessario per cadere quella distanza. Questo deriva dalle equazioni cinematiche del moto.
Mettendo tutto insieme si traduce in un'equazione per il momento di inerzia in termini di quantità misurabili durante l'esperimento:
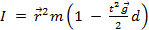 . (Equazione 7)
. (Equazione 7)
Se due masse sono attaccate al braccio rotante a distanze uguali ![]() dall'asse di rotazione, il momento di inerzia sarà:
dall'asse di rotazione, il momento di inerzia sarà:
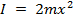 , (Equazione 8)
, (Equazione 8)
che è il valore teorico per questo esperimento.

Figura 1. Configurazione sperimentale.
Procedura
1. Misurare il momento di inerzia dell'asta lunga.
- Avvolgere la corda attaccata al peso fino a quando il peso è vicino al braccio rotante.
- Lascia cadere il peso e misura il tempo necessario per cadere, così come la distanza che scende.
- Eseguire il passaggio 1.2 tre volte e calcolare il momento medio di inerzia utilizzando l'equazione 7.
- Calcola il momento teorico di inerzia della canna da spinning usando la seguente formula:
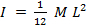 , dove è la massa
, dove è la massa  dell'asta e
dell'asta e 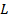 è la lunghezza.
è la lunghezza. - Confrontare il valore teorico con il valore misurato e registrare la differenza.
2. Due masse attaccate all'asta.
- Posizionare due masse da 100 kg a 20 cm di distanza dal centro dell'asta.
- Ripetere i passaggi 1.2 e 1.3 con le masse collegate.
- Il momento totale di inerzia dovrebbe essere uguale al momento di inerzia delle masse attaccate più il momento di inerzia dell'asta. Usa questo fatto, i risultati del passo 1 e l'equazione 8 per determinare i momenti teorici e sperimentali di inerzia per le masse attaccate.
- Confrontare i valori teorici con i valori misurati e registrare le differenze.
3. Effetto della distanza sul momento di inerzia.
- Ripetere il passaggio 2 del laboratorio, ma spostare le masse attaccate a 10 cm di distanza dal centro di rotazione. Notare eventuali cambiamenti nella caduta del peso o nella rotazione dell'asta.
- Confrontare i valori teorici con i valori misurati e registrare le differenze.
4. Effetto della massa sul momento di inerzia.
- Ripetere il passaggio 2 del laboratorio, ma modificare la dimensione della massa a 200 kg.
- Confrontare i valori teorici con i valori misurati e registrare le differenze.
Risultati
| Valore teorico
(kg m2) |
Valore sperimentale
(kg m2) |
Differenza
(%) |
|
| Parte 1 | 0.20 | 0.22 | 10 |
| Parte 2 | 0.08 | 0.07 | 14 |
| Parte 3 | 0.02 | 0.02 | 0 |
| Parte 4 | 0.16 | 0.15 | 6 |
I risultati dell'esperimento confermano le previsioni fatte dalle equazioni 7 e 8. Il momento di inerzia per una canna da spinning, come dato dalla formula nel passaggio 1.4, è stato confermato sperimentalmente. La distanza ridotta nel passaggio 3 ha comportato un momento di inerzia più piccolo, come previsto. La massa maggiore nel passaggio 4 ha provocato un momento di inerzia più grande, come previsto dall'equazione 8.
Applicazione e Riepilogo
Ti sei mai chiesto perché un funambolo porta un palo molto lungo? Il motivo è che il palo lungo ha un momento di inerzia molto grande a causa della sua lunghezza. Pertanto, richiede una grande quantità di coppia per farlo ruotare. Questo aiuta il funambolo a rimanere in equilibrio, poiché il palo rimarrà stabile.
Le ruote di auto e biciclette non sono mai solo dischi solidi; invece, hanno raggi che sostengono la ruota dall'asse. Ciò consente un design più leggero, che aiuta con la velocità, Tuttavia, la vera ragione di questo design può essere spiegata l'inerzia rotazionale. Un disco solido ha un momento di inerzia più grande di una forma a cerchio. Con il suo momento di inerzia più piccolo, un cerchio richiede meno coppia per girare e, forse ancora più importante, richiede meno coppia per smettere di girare.
Quando un giocatore di baseball è in battuta contro un lanciatore che lancia palle veloci, potrebbe voler accelerare il suo swing per ottenere un colpo. Può raggiungere questo obiettivo semplicemente avvicinando le mani all'estremità pesante del pipistrello, che si chiama "soffocamento". Ciò riduce la distanza dal centro di massa del pipistrello all'asse di rotazione e quindi rende più facile per la pastella ruotare il pipistrello.
In questo esperimento, il momento di inerzia per un'asta e due masse sono stati misurati sperimentalmente e calcolati teoricamente. Sono state esaminate le differenze tra questi valori. È stato testato l'effetto della massa sul momento di inerzia, così come l'effetto della distanza dall'asse di rotazione.
Vai a...
Video da questa raccolta:

Now Playing
Momento di inerzia
Physics I
43.8K Visualizzazioni

I principi della dinamica (leggi di Newton)
Physics I
76.9K Visualizzazioni

Forza e accelerazione
Physics I
79.7K Visualizzazioni

Vettori in più direzioni
Physics I
182.8K Visualizzazioni

Cinematica e moto parabolico
Physics I
73.1K Visualizzazioni

Legge di gravitazione universale di Newton
Physics I
192.8K Visualizzazioni

Conservazione del momento angolare
Physics I
43.6K Visualizzazioni

Attrito
Physics I
53.1K Visualizzazioni

Legge di Hooke e moto armonico semplice
Physics I
61.6K Visualizzazioni

Diagrammi di equilibrio e corpo libero
Physics I
37.6K Visualizzazioni

Momento meccanico
Physics I
26.2K Visualizzazioni

Momento angolare
Physics I
36.6K Visualizzazioni

Energia e lavoro
Physics I
50.4K Visualizzazioni

Entalpia
Physics I
60.6K Visualizzazioni

Entropia
Physics I
17.8K Visualizzazioni