Vektoren in mehrere Richtungen
Überblick
Quelle: Nicholas Timmons, Asantha Cooray, PhD, Department of Physics & Astronomie, School of Physical Sciences, University of California, Irvine, CA
Dieses Experiment zeigt, wie Vektoren addieren und subtrahieren in mehrere Richtungen. Das Ziel ist es, analytisch die Addition oder Subtraktion von mehreren Vektoren zu berechnen und dann die Berechnungen experimentell zu bestätigen.
Ein Vektor ist ein Objekt mit Größe und Richtung. Die Größe eines Vektors wird einfach als die Länge bezeichnet, während die Richtung in der Regel durch den Winkel definiert ist, macht es mit der X -Achse. Da Kräfte Vektoren sind, können sie als eine physische Darstellung von Vektoren verwendet werden. Durch die Einrichtung eines Systems der Kräfte und zu finden, welche zusätzliche Kraft ein Gleichgewicht zwischen den Kräften schaffen wird, kann ein System von Vektoren experimentell überprüft werden.
Grundsätze
In Abbildung 1 zeigt den Vektor  , sowie die x- und y -Achsen und Winkel θ, die
, sowie die x- und y -Achsen und Winkel θ, die  macht mit der X -Achse.
macht mit der X -Achse.

Abbildung 1 .
Zu addieren oder zu subtrahieren zweier Vektoren, ist es sinnvoll, den Vektor in Bezug auf die x- und y -Komponenten zu beschreiben. Die X -Komponente ist der Betrag des Vektors, der in X -Richtung, verweist die mathematisch als dargestellt wird:
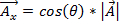 . (Gleichung 1)
. (Gleichung 1)
Die y -Komponente wird folgendermaßen dargestellt:
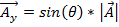 . (Gleichung 2)
. (Gleichung 2)
Das Ausmaß der  ist definiert:
ist definiert:
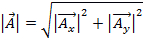 . (Gleichung 3)
. (Gleichung 3)
Zu addieren oder zu subtrahieren zweier Vektoren, einfach zerlegen Sie die Vektoren in ihre x- und y -Komponenten und dann addieren Sie oder subtrahieren Sie, bzw. die entsprechenden Komponenten.
Zum Beispiel wenn Vektor 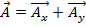 und Vektor
und Vektor 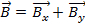 , dann die Zugabe der beiden Vektoren
, dann die Zugabe der beiden Vektoren  .
.
Um den Winkel θ bestimmen macht ein Vektor bezüglich der X -Achse, verwenden Sie die folgende Gleichung:
 . (Gleichung 4)
. (Gleichung 4)
Da Vektoren Größe und Richtung haben, ist es nicht so einfach wie die Multiplikation zweier Zahlen, Multiplikation zweier Vektoren. Es gibt zwei Möglichkeiten um Vektoren zu multiplizieren: das Skalarprodukt und das Kreuzprodukt. Das Skalarprodukt kann geschrieben werden, als 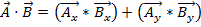 oder
oder 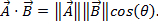 hier, θ ist der Winkel zwischen den beiden Vektoren. Das Ergebnis hat nur eine Größe, und keine Richtung. Eine Anwendung das Punktprodukt in der Physik ist Arbeit (W), wo Arbeit ist definiert als eine Kraft mal Abstand
hier, θ ist der Winkel zwischen den beiden Vektoren. Das Ergebnis hat nur eine Größe, und keine Richtung. Eine Anwendung das Punktprodukt in der Physik ist Arbeit (W), wo Arbeit ist definiert als eine Kraft mal Abstand 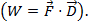 das Kreuzprodukt der beiden Vektoren kann als geschrieben werden
das Kreuzprodukt der beiden Vektoren kann als geschrieben werden 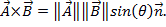 zwar ähnlich wie das Skalarprodukt, das Kreuzprodukt enthält den Begriff
zwar ähnlich wie das Skalarprodukt, das Kreuzprodukt enthält den Begriff  , die definiert ist als Vektor mit Magnitude 1, die senkrecht zu den beiden Vektoren ist
, die definiert ist als Vektor mit Magnitude 1, die senkrecht zu den beiden Vektoren ist  und
und  . Das Ergebnis des Kreuzprodukts ist ein Vektor. Ein Beispiel für das Kreuzprodukt in der Physik ist Drehmoment
. Das Ergebnis des Kreuzprodukts ist ein Vektor. Ein Beispiel für das Kreuzprodukt in der Physik ist Drehmoment  , das ist das Ergebnis einer Kraft mal Radius
, das ist das Ergebnis einer Kraft mal Radius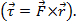
Vektoren sind nützlich in der Physik, weil Kräfte wie Schwerkraft oder Reibung als Vektoren dargestellt werden können. In dieser Übungseinheit wird der Schwerkraft zum demonstrieren der Vektor Art der Kräfte und wie jene Kräfte in mehrere Richtungen hinzufügen. Die Kraft von Schwerkraft auf der Erdoberfläche wird als geschrieben:
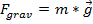 , (Gleichung 5)
, (Gleichung 5)
wo  ist die Masse des Objekts, während
ist die Masse des Objekts, während  ist die Beschleunigung durch die Schwerkraft in der Nähe der Erdoberfläche (9,8 m/s2).
ist die Beschleunigung durch die Schwerkraft in der Nähe der Erdoberfläche (9,8 m/s2).
Verfahren
1. Bilanz zwingt.
- Auf die Tabelle die zwei Riemenscheiben bei gleicher Masse nach entgegengesetzten Richtungen (180° Winkeldifferenz) eingerichtet.
- Die Kraft der einzelnen werden gleich
 . Überprüfen Sie, ob die zwei Kräfte sind gleiche und entgegengesetzte anhand des Ringes in der Mitte des Tisches Kraft, die sich nicht bewegen sollte.
. Überprüfen Sie, ob die zwei Kräfte sind gleiche und entgegengesetzte anhand des Ringes in der Mitte des Tisches Kraft, die sich nicht bewegen sollte. - Beachten Sie, dass wenn die Komponenten der Vektoren verbunden mit diesen Kräften hinzugefügt werden, wird der resultierende Vektor Null Größenordnung haben. Dies ist wie Sie feststellen können, dass alle Kräfte im Gleichgewicht befinden.
(2) analytische Berechnungen.
- Diese Übungseinheit besteht aus drei Kräfte im Gleichgewicht. Zwei Kräfte bekannt sein werden, während die dritte fanden erste analytisch, werden mit Hilfe der Theorie der Vektoren, und dann experimentell. Für diese Übungseinheit zu halten
 bei 0° für die Dauer.
bei 0° für die Dauer. - Beachten Sie, dass bei
 und
und  sind bekannt und
sind bekannt und  , wenn hinzugefügt, um das System, Ursachen, die die beiden Kräfte im Gleichgewicht, dann sein
, wenn hinzugefügt, um das System, Ursachen, die die beiden Kräfte im Gleichgewicht, dann sein  ist von gleicher Größe, aber in die entgegengesetzte Richtung der Summe (
ist von gleicher Größe, aber in die entgegengesetzte Richtung der Summe ( +
+  ).
). - Berechnen Sie die Größe des
 und
und  . Verwenden Sie die Tatsache, dass
. Verwenden Sie die Tatsache, dass  und 1 Newton (N) ist eine Einheit der Kraft gleich
und 1 Newton (N) ist eine Einheit der Kraft gleich  .
. - Mit Hilfe der Theorie der Vektoren, welche Größenordnung berechnen
 wäre, wenn es die Summe (
wäre, wenn es die Summe ( +
+  ).
). - Mit Hilfe der Theorie der Vektoren, welchem Winkel berechnen
 wäre, wenn es die Summe (
wäre, wenn es die Summe ( +
+  ).
).
(3) Experiment.
- Nach den Werten in der ersten Zeile der Tabelle 1 für
 und
und  , richten Sie die zwei Kräfte auf die Tabelle. Denken Sie daran,
, richten Sie die zwei Kräfte auf die Tabelle. Denken Sie daran,  bei 0°.
bei 0°. - Richten Sie die dritte Kraft,
 , durch Hinzufügen von Gewichten und den Winkel zu ändern, bis Gleichgewicht erreicht ist. Notieren Sie diese Werte in Tabelle 2.
, durch Hinzufügen von Gewichten und den Winkel zu ändern, bis Gleichgewicht erreicht ist. Notieren Sie diese Werte in Tabelle 2. - Wiederholen Sie Schritt 3.2 für jede der vier Fälle.
- Bestimmen den prozentuale Unterschied von dem Ergebnis der Analyse durch die Berechnung der
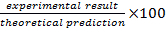 . Geben Sie in Tabelle 2 mit diesen berechneten Werten.
. Geben Sie in Tabelle 2 mit diesen berechneten Werten.
Ergebnisse
Die Ergebnisse des Labors sind in Tabelle 1 und Tabelle 2gezeigt.
Tabelle 1. Richten Sie ein.
| # Einrichten | A | B | ||
| Masse | Winkel | Masse | Winkel | |
| 1 | 100 | 0 | 100 | 20 |
| 2 | 100 | 0 | 150 | 40 |
| 3 | 200 | 0 | 150 | 60 |
| 4 | 200 | 0 | 250 | 80 |
Tabelle 2. Analyseergebnisse.
| # Einrichten | Größenordnung (N) |
Größenordnung (N) |
Winkel (°) |
Größenordnung (N) |
Winkel (°) |
| 1 | 0,98 | 0,98 | 20 | 1.93 | 10 |
| 2 | 0,98 | 1,47 | 40 | 2.31 | 24 |
| 3 | 1.96 | 1,47 | 60 | 2,98 | 25 |
| 4 | 1.96 | 2.45 | 80 | 3.39 | 45 |
Tabelle 3. Experimentelle Ergebnisse.
| # Einrichten | Experimentelle Größenordnung (N) |
Analytische Stärke (N) |
Unterschied (%) |
Experimentelle Winkel (°) |
Analytische Winkel (°) |
Unterschied (%) |
| 1 | 2.1 | 1.93 | 9 | 11 | 10 | 10 |
| 2 | 2.2 | 2.31 | 5 | 26 | 24 | 8 |
| 3 | 2.8 | 2,98 | 6 | 28 | 25 | 12 |
| 4 | 3.5 | 3.39 | 3 | 43 | 45 | 5 |
Die Ergebnisse des Experiments sind im Einvernehmen mit den analytischen Berechnungen. Die Summe der beiden Vektoren und die Winkel zwischen ihnen kann mit Gleichungen 1 bis 5berechnet werden. Die Gleichungen gelten für Berechnungen von physikalischen Vektoren, wie Kraft.
Anwendung und Zusammenfassung
Ein Outfielder im Baseball hat Vektoren zu verstehen, um unterwegs einen Ball fangen. Wenn die Outfielder nur die Geschwindigkeit des Balles kannte, könnte er zu Leftfield statt nach rechts laufen und verpassen den Ball. Wüsste er nur die Richtung der Hit, könnte er in, berechnen, nur um den Ball über den Kopf zu segeln zu sehen. Wenn er Vektoren versteht, kann dann, sobald der Ball getroffen wird, er prüfen, das Ausmaß und die Richtung um abzuschätzen, wo der Ball geht zu sein, wenn er einen Haken macht.
Wenn ein Flugzeug am Himmel steht, können seine Geschwindigkeit und Richtung als Vektor geschrieben werden. Wird ein starker Wind, des Windvektors verleiht der Vektor der Ebene, die daraus resultierende System Vektor zu geben. Z. B. wenn ein Flugzeug in den Wind fliegen, wird die Größe des resultierenden Vektors kleiner als die anfängliche Stärke sein. Dies entspricht das Flugzeug bewegt sich langsamer als in den Wind, die intuitiv Sinn macht.
Wenn zwei Objekte kollidieren und zusammenkleben, kann ihre endgültige Dynamik (ein Vektor) als die Summe der beiden ersten Schwung Vektoren angenähert werden. Dies ist eine Vereinfachung, wie in der realen Welt, zwei Objekte kollidieren haben zusätzliche Faktoren zu berücksichtigen, wie Hitze oder Verformung aus der Kollision. Momentum ist nur die Masse eines Körpers mit seiner Geschwindigkeit multipliziert. Wenn zwei Skater auf Eis Reisen in verschiedene Richtungen und mit unterschiedlichen Geschwindigkeiten kollidieren und einander festhalten, werden ihre endgültige Richtung und Geschwindigkeit je nach ihrer anfänglichen Vektorkomponenten abgeschätzt.
In diesem Experiment wurde die Vektor Art der Kräfte untersucht und gemessen. Vektoren wurden zusammengezählt und die daraus resultierende Größe und Richtung wurden sowohl analytisch als auch experimentell bestimmt.
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Vektoren in mehrere Richtungen
Physics I
182.7K Ansichten

Newtonsche Gesetze der Bewegung
Physics I
76.9K Ansichten

Kraft und Beschleunigung
Physics I
79.6K Ansichten

Kinematik und Projektilbewegung
Physics I
73.1K Ansichten

Newtonsches Gravitationsgesetz
Physics I
192.7K Ansichten

Der Impulserhaltung
Physics I
43.6K Ansichten

Reibung
Physics I
53.1K Ansichten

Hookesches Gesetz und harmonische Schwingungen
Physics I
61.6K Ansichten

Gleichgewichts- und Freikörper-Diagramme
Physics I
37.6K Ansichten

Drehmoment
Physics I
26.2K Ansichten

Rotationsträgheit
Physics I
43.8K Ansichten

Drehimpuls
Physics I
36.6K Ansichten

Energie und Arbeit
Physics I
50.4K Ansichten

Enthalpie
Physics I
60.6K Ansichten

Entropie
Physics I
17.8K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten