Inercia rotacional
Fuente: Nicolás Timmons, Asantha Cooray, PhD, Departamento de física & Astronomía, Facultad de ciencias física, Universidad de California, Irvine, CA
La inercia es la resistencia de un objeto a ser acelerado. En la cinemática lineal, este concepto está directamente relacionado con la masa de un objeto. El más masivo un objeto, más fuerza es necesaria para acelerar ese objeto. Esto se ve directamente en la segunda ley de Newton, que dice que fuerza es igual a la aceleración del tiempo de masa.
Para la rotación, hay un concepto similar que se denomina inercia rotacional. En este caso, la inercia rotacional es la resistencia de un objeto a ser rotatorio acelerado. Inercia rotacional depende no sólo la masa, sino también sobre la distancia de la masa desde el centro de rotación.
El objetivo de este experimento es medir la inercia rotacional de las masas giratorias dos y determinar la dependencia de la masa y la distancia desde el eje de rotación.
Un determinado objeto o sistema de objetos tiene cierta inercia rotacional. La inercia rotacional alrededor de un cierto eje se llama momento de inercia. Porque la distancia entre la masa y el eje de rotación es importante, un solo objeto puede tener diferentes momentos de inercia según el eje sobre el cual gira. El momento de inercia de un objeto se define como:
 , (Ecuación 1)
, (Ecuación 1)
donde i es el número de objetos.
En la ecuación 1, r es la distancia desde el eje de rotación de la masa. Como puede verse en la ecuación, el momento de inercia depende de la masa del objeto y el cuadrado de la distancia de la masa al eje de rotación.
Apenas como cómo lineal cinemática tiene ecuaciones de movimiento, cinemática rotacional tiene análogas ecuaciones de movimiento. Por ejemplo, la segunda ley de Newton para movimiento lineal es:
 . (Ecuación 2)
. (Ecuación 2)
Una ecuación similar rotación toma la forma:
 , (Ecuación 3)
, (Ecuación 3)
donde 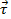 es el par,
es el par, 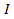 es el momento de inercia, y
es el momento de inercia, y  es la aceleración angular. Aquí, el momento de inercia es el análogo del término masas en segunda ley de Newton. Del mismo modo, el momento de inercia está presente en las otras importantes ecuaciones de movimiento de rotación:
es la aceleración angular. Aquí, el momento de inercia es el análogo del término masas en segunda ley de Newton. Del mismo modo, el momento de inercia está presente en las otras importantes ecuaciones de movimiento de rotación:
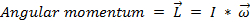 , (Ecuación 4)
, (Ecuación 4)
 , (Ecuación 5)
, (Ecuación 5)
donde 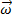 es la velocidad angular del objeto.
es la velocidad angular del objeto.
Para este experimento, una masa está conectada a un brazo giratorio por una cadena que se enrolla alrededor del eje de rotación. Vea la figura 1 para una imagen de como luce la instalación experimental. Dos masas se conectarán con el brazo rotatorio, fricción se omitirá en este experimento, y el momento de inercia total será igual a la hora de las masas giratorias más el momento del brazo de giro.
La masa, que se cae debido a la influencia de la gravedad, será aprobar una torsión en el brazo giratorio. De la ecuación 2,  y
y 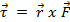 . Aquí,
. Aquí, 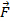 es la fuerza sobre el objeto, que viene de la tensión
es la fuerza sobre el objeto, que viene de la tensión 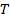 en la cadena, y
en la cadena, y  es la distancia desde la fuerza hasta el eje de rotación. Aquí, esa distancia es la distancia desde el borde de la cuerda enrollada en el eje de rotación.
es la distancia desde la fuerza hasta el eje de rotación. Aquí, esa distancia es la distancia desde el borde de la cuerda enrollada en el eje de rotación.
La aceleración angular  es definido por
es definido por  , donde
, donde  es la aceleración lineal de un punto en la cadena de herida que corresponde a la aceleración del peso descendente. Poniendo todo junto da
es la aceleración lineal de un punto en la cadena de herida que corresponde a la aceleración del peso descendente. Poniendo todo junto da 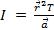 . Segunda ley de Newton se usa para encontrar la tensión. La suma de las fuerzas en el objeto debe ser igual a la masa la aceleración de las épocas. Aquí, las fuerzas del peso descendente son gravedad (
. Segunda ley de Newton se usa para encontrar la tensión. La suma de las fuerzas en el objeto debe ser igual a la masa la aceleración de las épocas. Aquí, las fuerzas del peso descendente son gravedad (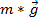 ) y la tensión
) y la tensión 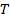 , tan
, tan 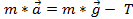 . Suponiendo una aceleración constante, luego
. Suponiendo una aceleración constante, luego 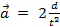 , donde
, donde  es la distancia que viaja el peso y
es la distancia que viaja el peso y  es el tiempo que tarda en caer esa distancia. Esto viene de las ecuaciones cinemáticas del movimiento.
es el tiempo que tarda en caer esa distancia. Esto viene de las ecuaciones cinemáticas del movimiento.
Poniendo todo junto da como resultado una ecuación para el momento de inercia en términos de cantidades que son medibles durante el experimento:
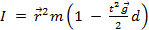 . (Ecuación 7)
. (Ecuación 7)
Si dos masas se unen al brazo de giro en distancias iguales ![]() del eje de rotación, entonces el momento de inercia será:
del eje de rotación, entonces el momento de inercia será:
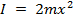 , (Ecuación 8)
, (Ecuación 8)
cual es el valor teórico para este experimento.

Figura 1. Disposición experimental.
1. medir el momento de inercia de la varilla larga.
- La cadena unida al peso hasta que el peso es cerca del brazo de giro del viento.
- El peso de la gota y medir el tiempo que toma para la gota, así como la distancia que cae.
- Realizar paso 1.2 tres veces y calcular el momento de inercia promedio utilizando la ecuación 7.
- Calcular el momento de inercia teórico de la barra de giro utilizando la siguiente fórmula:
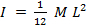 , donde
, donde  es la masa de la varilla y
es la masa de la varilla y 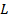 es la longitud.
es la longitud. - Comparar el valor teórico valor medido y registre la diferencia.
2. dos masas atadas a la barra.
- Colocar dos masas de 100 kg 20 cm lejos del centro de la varilla.
- Repita los pasos 1.2 y 1.3 con las masas adjuntadas.
- El momento de inercia total debe ser igual a la moment of inertia de las masas adjuntadas además el momento de inercia de la varilla. Utilice este hecho, los resultados del paso 1 y la ecuación 8 para determinar los momentos de inercia teóricas y experimentales para las masas adjuntadas.
- Comparar los valores teóricos con los valores medidos y anotar las diferencias.
3. efecto de la distancia en el momento de inercia.
- Repita el paso 2 del laboratorio, pero mover las masas acopladas a 10 cm de distancia del centro de rotación. Tenga en cuenta cualquier cambio en la caída del peso o el giro de la varilla.
- Comparar los valores teóricos con los valores medidos y anotar las diferencias.
4. efecto de masa en el momento de inercia.
- Repita el paso 2 del laboratorio, pero cambiar el tamaño de la masa a 200 kg.
- Comparar los valores teóricos con los valores medidos y anotar las diferencias.
| Valor teórico
(kg m2) |
Valor experimental
(kg m2) |
Diferencia
(%) |
|
| Parte 1 | 0.20 | 0.22 | 10 |
| Parte 2 | 0.08 | 0.07 | 14 |
| Parte 3 | 0.02 | 0.02 | 0 |
| Parte 4 | 0.16 | 0.15 | 6 |
Los resultados del experimento confirman las predicciones de las ecuaciones 7 y 8. El momento de inercia de una varilla de giro, según lo dado por la fórmula en el paso 1.4, fue confirmada experimentalmente. La distancia reducida en el paso 3 dio lugar a un menor momento de inercia, como se predijo. La masa más grande en el paso 4 dio lugar a un mayor momento de inercia, según lo predicho por la ecuación 8.
¿Te has preguntado ¿por qué un equilibrista lleva un palo muy largo? La razón es que el polo largo tiene un momento de inercia muy grande debido a su longitud. Por lo tanto, requiere una gran cantidad de esfuerzo de torsión para hacerlo girar. Esto ayuda al equilibrista para mantener el equilibrio, como el Polo se mantendrá constante.
Ruedas de coches y bicicletas nunca son discos sólo sólidos; en cambio, tienen radios compatibles con la rueda del eje. Esto permite un diseño más ligero, que ayudas con velocidad, sin embargo, la verdadera razón de este diseño puede ser explicado inercia rotacional. Un disco sólido tiene un mayor momento de inercia de una forma de aro. Con su menor momento de inercia, un aro requiere menos esfuerzo de torsión para girar y, quizás lo más importante, requiere menos esfuerzo de torsión deje de girar.
Cuando un jugador de béisbol batear contra un lanzador lanzar conectores FastBall, puede acelerar su swing para conseguir un éxito. Él puede lograr esto simplemente moviendo las manos más cerca al final pesado del murciélago, que se llama "asfixia para arriba." Esto reduce la distancia desde el centro de masa del murciélago al eje de rotación y por lo tanto facilita el bateador girar el palo.
En este experimento, el momento de inercia de una barra y dos masas se midieron experimentalmente y teóricamente calculadas. Se examinaron las diferencias entre estos valores. Se probó el efecto de masa en el momento de inercia, así como el efecto de la distancia desde el eje de rotación.
Saltar a...
Vídeos de esta colección:

Now Playing
Inercia rotacional
Physics I
43.5K Vistas

Las leyes del movimiento de Newton
Physics I
75.7K Vistas

Fuerza y aceleración
Physics I
79.1K Vistas

Vectores en múltiples direcciones
Physics I
182.3K Vistas

Cinemática y movimiento de proyectiles
Physics I
72.6K Vistas

Ley de la gravitación Universal de Newton
Physics I
190.8K Vistas

Conservación del momento
Physics I
43.3K Vistas

Fricción
Physics I
52.9K Vistas

Ley de Hooke y el movimiento armónico simple
Physics I
61.3K Vistas

Diagramas de equilibrio y de cuerpo libre
Physics I
37.3K Vistas

Esfuerzo torsional
Physics I
24.3K Vistas

Momento angular
Physics I
36.2K Vistas

Energía y trabajo
Physics I
49.7K Vistas

Entalpía
Physics I
60.4K Vistas

Entropía
Physics I
17.6K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados