Inércia Rotacional
Visão Geral
Fonte: Nicholas Timmons, Asantha Cooray, PhD, Departamento de Física & Astronomia, Escola de Ciências Físicas, Universidade da Califórnia, Irvine, CA
Inércia é a resistência de um objeto a ser acelerado. Na cinemática linear, esse conceito está diretamente relacionado com a massa de um objeto. Quanto mais massivo um objeto, mais força é necessária para acelerar esse objeto. Isso é visto diretamente na segunda lei de Newton, que afirma que a força é igual à aceleração de massa.
Para rotação, há um conceito semelhante chamado inércia rotacional. Neste caso, a inércia rotacional é a resistência de um objeto a ser acelerado rotacionalmente. A inércia rotacional depende não apenas da massa, mas também da distância da massa do centro de rotação.
O objetivo deste experimento é medir a inércia rotacional de duas massas rotativas e determinar a dependência da massa e distância do eixo de rotação.
Princípios
Um certo objeto ou sistema de objetos tem alguma inércia rotacional. A inércia rotacional sobre um certo eixo é chamada de momento de inércia. Como a distância da massa para o eixo de rotação é importante, um único objeto pode ter momentos muito diferentes de inércia dependendo do eixo sobre o qual ele gira. O momento de inércia para um objeto é definido como:
 , (Equação 1)
, (Equação 1)
onde eu sou o número de objetos.
Na Equação 1, r é a distância do eixo de rotação para a massa. Como pode ser visto na equação, o momento da inércia depende da massa do objeto e do quadrado da distância da massa ao eixo de rotação.
Assim como a cinemática linear tem equações de movimento, a cinemática rotacional tem equações análogas de movimento. Por exemplo, a segunda lei de Newton para o movimento linear é:
 . (Equação 2)
. (Equação 2)
Uma equação rotacional semelhante toma a forma:
 , (Equação 3)
, (Equação 3)
onde 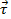 está o torque, é o momento da
está o torque, é o momento da 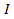 inércia, e
inércia, e  é a aceleração angular. Aqui, o momento da inércia é o analógico do termo de massa na segunda lei de Newton. Da mesma forma, o momento da inércia está presente nas outras equações importantes do movimento rotacional:
é a aceleração angular. Aqui, o momento da inércia é o analógico do termo de massa na segunda lei de Newton. Da mesma forma, o momento da inércia está presente nas outras equações importantes do movimento rotacional:
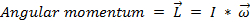 , (Equação 4)
, (Equação 4)
 , (Equação 5)
, (Equação 5)
onde 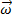 está a velocidade angular do objeto.
está a velocidade angular do objeto.
Para este experimento, uma massa é conectada a um braço rotativo por uma corda ferida ao redor do eixo de rotação. Consulte a Figura 1 para obter uma imagem de como é a configuração experimental. Duas massas serão conectadas ao braço rotativo, o atrito será ignorado neste experimento, e o momento total da inércia será igual ao momento das massas rotativas mais o momento do braço giratório.
A massa, que cai devido à influência da gravidade, decretará um torque no braço rotativo. Da Equação 2,  e
e 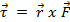 . Aqui,
. Aqui, 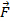 está a força no objeto, que vem da tensão na
está a força no objeto, que vem da tensão na 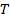 corda, e é a distância da força
corda, e é a distância da força  para o eixo de rotação. Aqui, essa distância é a distância da borda da corda da ferida até o eixo de rotação.
para o eixo de rotação. Aqui, essa distância é a distância da borda da corda da ferida até o eixo de rotação.
A aceleração angular  é definida por , onde está a
é definida por , onde está a 
 aceleração linear de um ponto na corda da ferida que corresponde à aceleração do peso em queda. Juntar tudo
aceleração linear de um ponto na corda da ferida que corresponde à aceleração do peso em queda. Juntar tudo 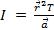 dá. A segunda lei de Newton é usada para encontrar a tensão. A soma das forças no objeto deve ser igual à massa vezes a aceleração. Aqui, as forças sobre o peso em queda são a gravidade
dá. A segunda lei de Newton é usada para encontrar a tensão. A soma das forças no objeto deve ser igual à massa vezes a aceleração. Aqui, as forças sobre o peso em queda são a gravidade 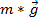 e a
e a 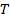 tensão, então
tensão, então 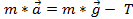 . Assumindo uma aceleração constante,
. Assumindo uma aceleração constante, 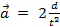 então, onde
então, onde  está a distância que o peso percorre e é o tempo que leva para cair essa
está a distância que o peso percorre e é o tempo que leva para cair essa  distância. Isso vem das equações cinemáticas do movimento.
distância. Isso vem das equações cinemáticas do movimento.
Juntar tudo resulta em uma equação para o momento da inércia em termos de quantidades mensuráveis durante o experimento:
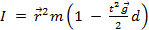 . (Equação 7)
. (Equação 7)
Se duas massas estiverem presas ao braço giratório a distâncias iguais ![]() do eixo de rotação, então o momento da inércia será:
do eixo de rotação, então o momento da inércia será:
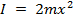 , (Equação 8)
, (Equação 8)
que é o valor teórico para este experimento.

Figura 1. Configuração experimental.
Procedimento
1. Meça o momento de inércia da haste longa.
- Enrole a corda presa ao peso até que o peso esteja perto do braço giratório.
- Solte o peso e meça o tempo que leva para cair, assim como a distância que ele cai.
- Realize a etapa 1.2 três vezes e calcule o momento médio da inércia usando a Equação 7.
- Calcule o momento teórico da inércia da haste giratória usando a seguinte fórmula:
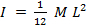 , onde está a massa da
, onde está a massa da  haste e é o
haste e é o 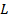 comprimento.
comprimento. - Compare o valor teórico com o valor medido e regisse a diferença.
2. Duas massas presas à haste.
- Coloque duas massas de 100 kg a 20 cm do centro da haste.
- Repita as etapas 1.2 e 1.3 com as massas anexadas.
- O momento total da inércia deve ser igual ao momento de inércia das massas anexadas mais o momento de inércia da haste. Use este fato, os resultados da etapa 1 e da Equação 8 para determinar os momentos teóricos e experimentais de inércia para as massas anexadas.
- Compare os valores teóricos com os valores medidos e regise as diferenças.
3. Efeito da distância no momento da inércia.
- Repita o passo 2 do laboratório, mas mova as massas anexadas para 10 cm de distância do centro de rotação. Observe quaisquer alterações na queda do peso ou na fiação da haste.
- Compare os valores teóricos com os valores medidos e regise as diferenças.
4. Efeito da massa no momento da inércia.
- Repita o passo 2 do laboratório, mas mude o tamanho da massa para 200 kg.
- Compare os valores teóricos com os valores medidos e regise as diferenças.
Resultados
| Valor Teórico
(kg m2) |
Valor Experimental
(kg m2) |
Diferença
(%) |
|
| Parte 1 | 0.20 | 0.22 | 10 |
| Parte 2 | 0.08 | 0.07 | 14 |
| Parte 3 | 0.02 | 0.02 | 0 |
| Parte 4 | 0.16 | 0.15 | 6 |
Os resultados do experimento confirmam as previsões feitas pelas Equações 7 e 8. O momento de inércia para uma haste giratória, como dado pela fórmula na etapa 1.4, foi confirmado experimentalmente. A distância reduzida na etapa 3 resultou em um momento menor de inércia, como previsto. A maior massa na etapa 4 resultou em um momento maior de inércia, como previsto pela Equação 8.
Aplicação e Resumo
Você já se perguntou por que um andarilho da corda bamba carrega uma vara muito longa? A razão é que o polo longo tem um momento muito grande de inércia devido ao seu comprimento. Portanto, requer uma grande quantidade de torque para fazê-lo girar. Isso ajuda o andador da corda bamba a se manter equilibrado, pois o poste permanecerá estável.
Rodas de carros e bicicletas nunca são apenas discos sólidos; em vez disso, eles têm raios que suportam a roda do eixo. Isso permite um design mais leve, que auxilia na velocidade, no entanto, a verdadeira razão para este design pode ser explicada inércia rotacional. Um disco sólido tem um momento maior de inércia do que uma forma de aro. Com seu menor momento de inércia, um aro requer menos torque para girar e, talvez mais importante, requer menos torque para parar de girar.
Quando um jogador de beisebol está no bastão contra um arremessador jogando bolas rápidas, ele pode querer acelerar seu balanço a fim de obter um hit. Ele pode conseguir isso simplesmente movendo as mãos para mais perto da extremidade pesada do morcego, que é chamado de "sufocamento". Isso reduz a distância do centro de massa do morcego para o eixo de rotação e, portanto, facilita a rotação do bastão.
Neste experimento, o momento de inércia para uma vara e duas massas foram medidos experimentalmente e teoricamente calculados. As diferenças entre esses valores foram examinadas. Foi testado o efeito da massa no momento da inércia, bem como o efeito da distância do eixo de rotação.
Pular para...
Vídeos desta coleção:

Now Playing
Inércia Rotacional
Physics I
43.5K Visualizações

Leis do Movimento de Newton
Physics I
75.7K Visualizações

Força e Aceleração
Physics I
79.1K Visualizações

Vetores em Múltiplas Direções
Physics I
182.3K Visualizações

Cinemática e Movimento de Projéteis
Physics I
72.6K Visualizações

Lei da Gravitação Universal de Newton
Physics I
190.8K Visualizações

Conservação do Momento
Physics I
43.3K Visualizações

Atrito
Physics I
52.9K Visualizações

Lei de Hooke e Movimento Harmônico Simples
Physics I
61.3K Visualizações

Diagramas de Equilíbrio e de Corpo Livre
Physics I
37.3K Visualizações

Torque
Physics I
24.3K Visualizações

Momento Angular
Physics I
36.2K Visualizações

Energia e Trabalho
Physics I
49.7K Visualizações

Entalpia
Physics I
60.4K Visualizações

Entropia
Physics I
17.6K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados