Entropie
Überblick
Quelle: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Department of Physics & Astronomie, School of Physical Sciences, University of California, Irvine, CA
Der zweite Hauptsatz der Thermodynamik ist ein Grundgesetz der Natur. Es besagt, dass die Entropie eines Systems immer erhöht sich im Laufe der Zeit oder im Idealfall konstant bleibt, wenn ein System in einen stabilen Zustand oder in einem "reversibler Prozess." Wenn das System einen unumkehrbaren Prozess unterzogen wird, wird die Entropie des Systems immer erhöht. Dies bedeutet, dass die Änderung der Entropie, ΔS, immer größer oder gleich Null ist. Die Entropie eines Systems ist ein Maß für die Anzahl der mikroskopische Konfigurationen, die das System erreichen kann. Gas in einem Behälter mit bekanntem Volumen, Druck und Temperatur können z. B. eine enorme Anzahl von möglichen Konfigurationen der einzelnen Gasmoleküle. Wenn der Container geöffnet wird, die Gasmoleküle entkommen und die Anzahl der Konfigurationen steigt dramatisch, im wesentlichen nähert sich unendlich. Wenn der Container geöffnet wird, soll die Entropie zu erhöhen. Daher kann Entropie ein Maß für die "Störung" eines Systems betrachtet werden.
Grundsätze
Entropie ist eine "State-Eigenschaft," die eine Menge, die nur von den aktuellen Zustand des Systems abhängt. Mengen Zustandeigenschaften richten sich nicht auf dem Weg, durch die das System in seinem gegenwärtigen Zustand angekommen. Daher ist der nützlichste Weg, eine State-Eigenschaft zu quantifizieren, seine ändernzu messen.
Die Änderung der Entropie S ist definiert als:
ΔS = Q / T, (Gleichung 1)
wo Q wird die Wärme an das System geliefert und T ist die Temperatur des Systems. Im Rahmen der Thermodynamik ist Hitze, wie Arbeit, definiert als eine Übertragung von Energie. Wärme ist Energie, die durch einen Unterschied in der Temperatur von einem Objekt auf ein anderes übertragen. Betrachten Sie ein Bad aus Eis und Wasser bei 0 ° C. Liefert eine Wärme an das Eis/Wasser-Bad, einige der das Eis schmilzt, und die Zahl der Staaten zur Verfügung, um die Wassermoleküle werden durch eine große Menge proportional zu der Menge an Wärme, die dem System hinzugefügt wurde. Die Entropie steigt proportional zu diesem Betrag. Die Beziehung zwischen zwei Objekten mit unterschiedlichen Temperaturen wurde zuerst von Newton beschrieben.
Gesetz des Newtons des Abkühlens besagt, dass die Änderungsrate der Temperatur eines Objekts proportional zur Differenz zwischen eigenem und der Temperatur der Umgebung. Für ein Objekt bei Temperaturen, die in einem geschlossenen System bei Temperatur Tf, diese Änderung in der Temperatur als Funktion der Zeit T gelegt wird t durch die Differentialgleichung beschrieben:
dT/dt = -k (T - T-f ), (Gleichung 2)
wo k ist eine konstante, die die Eigenschaften des Objekts und seiner Umgebung abhängt. Gleichung 1 wird als gleichwertig geschrieben:
-k dt = dT / (T - T-f ). (Gleichung 3)
Integration von beiden Seiten gibt:
-k t = Log (T - T-f ) + log C. (Gleichung 4)
Anwendung der Exponentialfunktion auf beide Seiten der Gleichung und dann neuordnen gibt:
T - T-f = C e-kt . (Gleichung 5)
Wenn das betreffende Objekt an eine Anfangstemperatur Tich zur Zeit ist t = 0:
TIch- Tf = C. (Gleichung 6)
Daraus folgt, dass die Temperatur als Funktion der Zeit:
T(t) = Tf + (TIch- Tf ) e-kt . (Gleichung 7)
Daher, wenn ein heißes Objekt in einem Kühler geschlossenen System platziert wird, sinkt seine Temperatur mit einer exponentiellen Rate. In diesem geschlossenen System wird die Wärme aus dem heißen Objekt Q erhöhen die Temperatur der kühleren Umgebung und damit erhöhen Sie die Anzahl der verfügbaren Staaten. Damit die Änderung der Entropie, ΔS, ist positiv und ungleich Null.
Verfahren
1. Setup.
- Zu erhalten, ein Heizelement und Stand, ein Thermometer, eine Stoppuhr, ein paar Papiertücher, Wasser und einen großen Becher.
- Das Becherglas mit ausreichend Wasser füllen, damit die Probe nicht zu schnell abkühlen wird (d. h. mindestens 500 mL).
- Stellen Sie den Becher mit Wasser gefüllt auf dem Stand unter dem Heizelement und schalten Sie ihn ein.
- Sobald das Becherglas Wasser kochen erreicht, legen Sie das Thermometer und schalten Sie das Heizelement.
- Sorgfältig entfernen Sie das Becherglas von der Heizung Stand und legen Sie es auf dem Tisch, auf das Küchenpapier. Diese fungieren als Isolierung aus der Tabelle.
2. Erfassung von Daten.
- Starten der Stoppuhr und notieren Sie die Temperatur und Zeit.
- Nehmen Sie für die ersten 20 min eine Messung über alle 1 Minuten.
- Nehmen Sie für die nächsten 20 min eine Messung über alle 3-5 Minuten.
- Notieren Sie diese Werte in Tabelle 1.
- Plot der Datenpunkte, die in Tabelle 1 in einem Diagramm Temperatur im Vergleich zur Zeit. gesammelt wurden
- Verwenden die Anfangstemperatur des Wassers und zwei Datenpunkte für Zeit und Temperatur, lösen Sie Gleichung 7 für die Kühlung Konstante k.
- Verwenden diesen Wert für k, Plot Gleichung 7 als eine stetige Funktion von t. Vergleichen Sie die Funktion mit den Datenpunkten, die gesammelt wurden.
Ergebnisse
Repräsentative Ergebnisse für 680 mL des Wassers sind in Tabelle 1dargestellt. Die Kühlung Konstante k wurde mithilfe der Datenpunkte in der Tabelle und die Lösung der Gleichung 7gefunden. Nach 35 min, T(35) = 50,6. War die anfängliche Temperatur 100 ° C, und Datenerhebung, die nicht mehr bei 28,5 ° C. Mit dieser Variablen gibt die folgende Gleichung, k: zu erhalten
50,6 = 28,5 + (100-28,5) e-k 35. (Gleichung 8)
Lösung für k einen Wert k gibt = 0,034. Die Kurve mit dieser Kühlung Konstante wird als gestrichelte graue Linie in Abbildung 1, zusammen mit den Datenpunkten aus dem Experiment gezeigt. Die funktionale Form der Gleichung 6 entspricht die experimentellen Ergebnissen sehr eng.
Während das Wasser abkühlt, abnimmt die Entropie, da die Anzahl der Staaten zur Verfügung, um die Wasser-Moleküle abnimmt. Die Entropie der Umgebungsluft im Raum erhöht, da die Wasserbecher Wärme auf die umgebenden Luftmoleküle überträgt; die gesamte Entropie des Wassers + air System erhöht. Die Zahl der Staaten, die jetzt heißer Luftmoleküle zu besetzen ist viel höher als, bevor das heiße Wasser in den Raum eingeführt wurde.
Differentielle Form die Hitze-d, die q hinzugefügt oder entfernt aus dem Wasser, kann unter Zugrundelegung der Beziehung zwischen Masse, spezifische Wärme c, berechnet und Temperaturänderung:
dQ = Mc dT, (Gleichung 9)
wo c 4,18 J/(gK) für Wasser werden bekannt. Die Änderung der Entropie des Wassers ist dann:
ΔSWasser =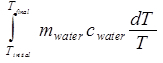
= mWasser cWasser ln (T final/Terste). (Gleichung 10)
Mit der Umstellung auf Kelvin als K = ° C + 273.15, die Änderung in der Entropie des Wassers wie folgt berechnet:
ΔSWasser = 680 g * 4,18 J /(g K) * ln [(28.5 + 273.15) / (100 + 273.15)]
=-604 J/K.
Die Temperatur der Umgebungsluft ist bei 20,4 ° C konstant, so ist dies ein isothermer Prozess. Die Entropie-Änderung der Luft ist dann:
ΔSLuft = 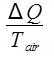 ,
,
wo Q ist die Abwärme von Wasser, das durch Gleichung 9gegeben ist. Die Änderung der Entropie der Luft ist dann wie folgt berechnet:
ΔSLuft =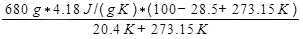
= 3337 J/K.
Die totale Veränderung in der Entropie des Wasser + Luft-System, ΔSTot, ist die Summe der einzelnen Veränderungen in der Entropie des Wassers und der Luft:
ΔSTot = ΔSWasser + ΔSLuft (Gleichung 11)
=-604 J/k + 3337 J/K
= 2733 J/K.
Tabelle 1. Temperaturen während des Experiments aufgezeichnet.
| Zeit (min s) | Wassertemperatur (° C) |
| 0 0 | 99,6 |
| 1-10 | 97,1 |
| 1-50 | 94,2 |
| 2 30 | 91,8 |
| 3-22 | 89 |
| 4-05 | 87,2 |
| 5 08 | 82,7 |
| 6 05 | 82,4 |
| 8-25 | 78 |
| 9-15 | 76,5 |
| 10 15 | 74,6 |
| 11 38 | 72,7 |
| 12 58 | 70,7 |
| 13 58 | 69,2 |
| 15 15 | 67,7 |
| 16 55 | 65,8 |
| 18 38 | 64 |
| 20 25 | 62,3 |
| 24 02 | 58,8 |
| 25 45 | 57,3 |
| 34 45 | 50,6 |
| 40 50 | 47,4 |
| 44 30 | 45.9 |
| 49 59 | 43.6 |
| 53 42 | 42,4 |
| 60 01 | 40,2 |
| 64 20 | 39,5 |
| 76 37 | 37 |
| 103-50 | 32.1 |
| 116 41 | 30.3 |
| 122 46 | 29,6 |
| 134 11 | 28.5 |

Abbildung 1 . Handlung der Temperatur im Vergleich zur Zeit. Die blauen Punkte zeigen die experimentellen Daten, und die gestrichelte Linie stellt theoretische Daten basierend auf Newtons Gesetz der Kühlung.
Anwendung und Zusammenfassung
Ein paar Kopfhörer, die immer in einer Tasche aufbewahrt werden tendenziell verknotet, das ist einer Zunahme der Entropie durch die Tragetasche herum verursacht. Es ist notwendig zu tun Arbeit am Kopfhörer zu un-Knoten sie und Abnahme die Entropie (Dies kann als eine "umkehrbares" betrachtet werden). Die effizienteste Wärmekreislauf Motor von physikalischen Gesetzen erlaubt ist der Carnot-Prozess. Der zweite Hauptsatz besagt, dass nicht alle für eine Wärmekraftmaschine zugeführte Wärmemenge verwendet werden kann, Arbeit zu verrichten. Der Carnot-Wirkungsgrad legt den Grenzwert auf den Anteil der Wärme, die verwendet werden kann. Der Zyklus besteht aus zwei isothermen Prozessen, gefolgt von zwei adiabatische Prozesse. Ein Kühlschrank, der im Wesentlichen nur eine Wärmepumpe ist, ist auch ein klassisches Beispiel des zweiten Hauptsatzes. Kühlschränke bewegen Wärme von einem Ort bei einer niedrigeren Temperatur (die "Quelle") an einen anderen Ort bei einer höheren Temperatur ("Heat Sink") mit mechanischer Arbeit. Entsprechend dem zweiten Gesetz fließen nicht Wärme von einem kälteren Ort zu einer heißer spontan; Arbeit (Energie) ist erforderlich für die Kältetechnik.
Gesetz des Newtons des Abkühlens zeigte einen Becher voll Wasser bei 100 ° C abkühlen auf Raumtemperatur, führte zu einer Zunahme der Entropie des Wasser-Luft-System. Durch die Messung der Temperatur des Wassers als Funktion der Zeit über einen Zeitraum von 135 min, war es möglich, die bestätigen, dass die Kühlung des Wassers exponentielle Form war. Die kühle Konstante der Wasserprobe wurde durch das Lösen der Kühlungen Gleichung mit gesammelten Daten gefunden.
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Entropie
Physics I
17.8K Ansichten

Newtonsche Gesetze der Bewegung
Physics I
76.9K Ansichten

Kraft und Beschleunigung
Physics I
79.6K Ansichten

Vektoren in mehrere Richtungen
Physics I
182.7K Ansichten

Kinematik und Projektilbewegung
Physics I
73.1K Ansichten

Newtonsches Gravitationsgesetz
Physics I
192.7K Ansichten

Der Impulserhaltung
Physics I
43.6K Ansichten

Reibung
Physics I
53.1K Ansichten

Hookesches Gesetz und harmonische Schwingungen
Physics I
61.6K Ansichten

Gleichgewichts- und Freikörper-Diagramme
Physics I
37.6K Ansichten

Drehmoment
Physics I
26.2K Ansichten

Rotationsträgheit
Physics I
43.8K Ansichten

Drehimpuls
Physics I
36.6K Ansichten

Energie und Arbeit
Physics I
50.4K Ansichten

Enthalpie
Physics I
60.6K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten