ソース:ニコラス ・ ティモンズ、 Asantha Cooray、PhD、物理教室 & 天文学、物理的な科学の学校、カリフォルニア大学、アーバイン、カリフォルニア州

慣性加速する物体の抵抗であります。直線運動でこの概念は直接オブジェクトの質量に関連します。オブジェクトより多くの力をより大規模なオブジェクトを加速する必要があります。これはニュートンの第 2 法則は、力は質量と加速度と等しい状態で直接見られます。

回転、回転慣性という似たようなコンセプトがあります。この場合、回転の慣性は加速されて回転する物体の抵抗です。回転慣性は回転の中心から質量の距離にも、質量だけでなく依存です。

この実験の目的は 2 つの回転固まりの回転慣性を測定し、質量と回転の軸からの距離に依存を決定します。

特定のオブジェクトまたはオブジェクトのシステムにはいくつかの回転慣性があります。特定の軸についての回転の慣性モーメントと呼びます。質量から回転軸までの距離が重要なために、単一のオブジェクトは回転する軸によって非常に異なる慣性モーメントを持つことができます。オブジェクトの断面 2 次モーメントは、として定義されます。

、 (関係式 1)

オブジェクトの数が。

式 1、 rは質量と回転の軸からの距離です。式でわかるように、慣性モーメントは質量から回転軸までの距離の二乗と物体の質量に依存しています。

回転運動は、類似運動方程式だけどのように線形運動のように運動方程式がある。たとえば、直線的な動きのニュートンの第 2 法則です。

.(式 2)

同じような回転式になります。

、 (式 3)

どこ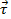トルクは、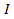は慣性モーメントとは角加速度。ここでは、慣性モーメントでは、ニュートンの第二法則が質量項のアナログ。同様に、慣性モーメントは回転運動の他の重要な方程式であります。

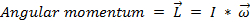、 (関係式 4)

、 (式 5)

どこ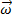オブジェクトの角速度です。

この実験のため質量は文字列の傷の回転の軸線のまわりで回転するアームに接続されます。実験のセットアップのように見える像は、図 1を参照してください。回転アームに接続される 2 つの質量、摩擦はこの実験で無視され、総慣性モーメントは回転の固まりの瞬間プラス回転アームの瞬間に等しくなります。

質量は、重力の影響のために落ちる、回転アームのトルクを制定します。方程式 2、 、 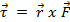。ここでは、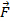緊張から来るオブジェクトの力は、 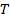、文字列内と力から回転軸までの距離です。ここでは、その距離は回転の軸に巻き弦の端からの距離です。

角加速度によって定義された、どこで落下重量加速度に対応する巻き弦上のポイントの線形加速です。一緒にすべてを置く与える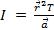。ニュートンの第 2 法則は、緊張を見つけるためです。オブジェクトの力の合計は、質量と加速度と等しくする必要があります。ここで、落下の重量力は重力 (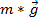) と緊張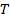、 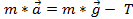。一定の加速度を想定して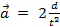、重量が移動する距離とその距離を落下するのにかかる時間です。これは、運動の運動方程式から来ています。

実験では測定可能な量の面で慣性モーメントの式を結果一緒にすべてを置きます。

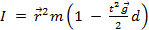.(関係式 7)

2 つの質量が等しい距離で回転アームに接続されているかどうか、回転軸から慣性モーメントになります。

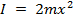、 (関係式 8)

この実験の理論値であります。

図 1。実験のセットアップ。

1. 長い棒の慣性モーメントを測定します。

1. 風重量は回転に腕の近くまで重量に接続されている文字列。
2. 体重を落とすし、削除にかかる時間だけでなく、ドロップ距離を測定します。
3. 手順 1.2 3 倍の慣性モーメントは、式 7を使用して、平均を計算します。
4. 次の数式を使用して回転ロッドの理論的な慣性モーメントを計算: 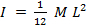、ロッドの質量と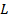長さです。
5. 実測値と理論値を比較し、違いを記録します。

2. 2 つの塊をロッドに接続されています。

1. ロッドの中心から離れた場所に 2 つの 100 kg 質量 20 cm。
2. 1.2 と 1.3 添付の固まりとの手順を繰り返します。
3. 総慣性モーメントは、接続されている大衆の moment of inertia プラス棒の慣性モーメントに等しいはずです。この事実、ステップ 1 と式 8からの結果を使用して、接続されている大衆のため理論的・実験的瞬間の慣性を決定します。
4. 実測値と理論値を比較し、相違点を記録します。

3. 距離の慣性モーメントに与える影響。

1. 演習の手順 2 を繰り返しますが、回転の中心から 10 cm に接続されている大衆を移動します。重量やロッドの回転の立ち下がりの変化に注意します。
2. 実測値と理論値を比較し、相違点を記録します。

4. 質量慣性モーメントの効果。

1. 演習の手順 2 を繰り返しますが、大容量サイズを 200 kg に変更します。
2. 実測値と理論値を比較し、相違点を記録します。

	理論値 (kg m2)	実験値 (kg m2)	違い (%)
パート 1	0.20	0.22	10
パート 2	0.08	0.07	14
その 3	0.02	0.02	0
その 4	0.16	0.15	6

実験の結果は、式 7 、 8によってなされる予言を確認します。1.4 の手順で数式によって指定された、回転棒の慣性モーメントは実験する.手順 3 で距離が短縮の結果、小さな慣性モーメント、予想通り。手順 4 で質量が大きいが、大きい慣性モーメント、方程式 8によって予測された結果になった

綱渡りをする軽業師が非常に長い棒を運ぶ理由を疑問があります?理由は、長い棒がその長さのために非常に大きな慣性モーメントを持っていることです。したがって、多量に回転トルクが必要です。これにより、ポールは堅調を保つ、バランスの取れた滞在する綱渡り。

車や自転車の車輪はありませんちょうど固体ディスク;代わりに、彼らは車軸からホイールをサポートするスポークがあります。これにより、軽量化設計の回転慣性を説明した速度、しかし、アクセシビリティ機能がこのデザインの本当の理由をすることができます。固体ディスクには、フープ状の形よりも大きな慣性モーメントがあります。フープはその小さいモーメントと回転以下のトルクを必要とし、おそらくもっと重要なは、回転が停止するより少ないトルクを必要とします。

野球選手は打席で速球を投げる投手に対して、彼いる場合は、ヒットを得るために彼のスウィングを高速化できます。彼は」窒息"と呼ばれるバットの重い終わりに近い彼の手を単に移動によってこれを達成することができます。これは回転の軸にバットの重心からの距離を短縮します、したがって、バットを回転するねり粉が容易になります。

この実験では、ロッドの断面 2 次モーメントと 2 つの質量の実験的測定し、理論的に計算。これらの値の違いを調べた。質量慣性モーメントの効果は、回転の軸からの距離の影響だけでなく、テストされました。