Hookesches Gesetz und harmonische Schwingungen
Quelle: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Department of Physics & Astronomie, School of Physical Sciences, University of California, Irvine, CA
Potentielle Energie ist ein wichtiges Konzept in der Physik. Potentielle Energie ist die Energie im Zusammenhang mit Kräften, die die Position eines Objekts relativ zu seiner Umgebung abhängig. Potenzielle Energie, die in einem anderen video diskutiert wird, ist die Energie verbunden, die direkt proportional zur Höhe eines Objekts über dem Boden ist. Ebenso ist es möglich, Frühling potentielle Energie, definieren die ist direkt proportional zur Vertreibung von einer Quelle aus seinen entspannten Zustand. Eine Feder gedehnte oder komprimierte hat potentielle Energie, da es die Fähigkeit, auf ein Objekt arbeiten zu tun hat. Die "Fähigkeit, Arbeit zu verrichten" wird oft als die grundlegende Definition von Energie veranschlagen.
Dieses Video veranschaulicht die potentielle Energie gespeichert in Federn. Es überprüft auch die Wiederherstellung Kraft Gleichsetzung von Federn oder Hookes Gesetz. Die Federkonstante ist für Quellen mit unterschiedlichen Elastizitäten unterschiedlich. Hookes Gesetz überprüft werden und die Federkonstante gemessen von unterschiedlichem Gewicht zu einer schwebenden Feder anbringen und die daraus resultierenden Verschiebungen zu messen.
Hält eine Feder entweder seine komprimierte oder gedehnte Position erfordert, dass jemand oder etwas eine Kraft auf die Feder übt. Diese Kraft ist proportional zur Vertreibung, Δy, des Frühlings. Wiederum wird die Feder ausüben, eine gleiche und entgegengesetzte Kraft:
F = -k Δy, (Gleichung 1)
wo k wird genannt die "Steifigkeit Federkonstante." Dies wird oft bezeichnet als "Rückstellkraft" weil die Feder eine Kraft in die Richtung der Verschiebung übt durch das negativen Vorzeichen angegeben. Gleichung 1 wird als Hookes Gesetz bezeichnet.
Einfache harmonische Bewegung wird auftreten, wenn es eine Rückstellkraft, die proportional zur Vertreibung von Gleichgewicht gibt, wie im Gesetz Hookes ist. Von Newtons zweites Gesetz, F = Ma, und der Erkenntnis, dass die Beschleunigung einer ist die zweite Ableitung der Verschiebung in Bezug auf Zeit, Gleichung 1 kann als umgeschrieben werden:
m (d2y/dt2) = -k-y. (Gleichung 2)
Die Lösung für das Differential zweiter Ordnung ist bekannt sein:
y (t) = Sünde (ωt + φ) (Gleichung 3)
wo A die Amplitude der Schwingung, ω ist = (k/m)1/2und der Phase Winkel φ , hängt von den Anfangsbedingungen des Systems. Gleichungen in Form von Gleichung 3 beschreiben was einfache harmonische Bewegung genannt wird. Die Periodendauer T, beziehen sich die Frequenz fund der konstante ω durch:
Ω = 2πf = 2π/T. (Gleichung 4)
Damit ist die Periodendauer T gegeben durch:
T = 2π (m/k)1/2. (Gleichung 5)
Beachten Sie, dass T nicht auf die Amplitude A der Schwingung abhängt. Daher, wenn eine Gewicht aus einer Quelle, unterbrochen von der vertikalen gehangen wird, wäre der resultierende Periode der Schwingung proportional zur Quadratwurzel der angehängten Gewicht.
Der Aufwand, den Frühling zu dehnen ist ein Abstand y W = <F> y, wo <F> ist die durchschnittliche Kraft erforderlich, um die Zeichenfolge zu dehnen. Da F in ylinear ist, ist im Durchschnitt nur die Kraft im Gleichgewicht (= 0) und die Kraft bei y:
<F> ½ = [0 + ky]. (Gleichung 6)
Die Arbeit und damit die elastische potentielle Energie, PE, können als geschrieben werden:
PE = ½ k y2. (Gleichung 7)
Die potenzielle Energie einer Feder wird in diesem Labor gemessen werden.
1. Messen Sie die Federkonstante und potenzielle Energie einer Feder und bestätigen Sie die Beziehung zwischen der Masse und oszillierenden Periode T.
- Erhalten Sie eine Feder mit einer bekannten Federkonstante, einen Stand, um den Frühling zu befestigen, mindestens 5 Gewichte der unterschiedlichen Massen, die Feder, ein Meter Stock und eine Stoppuhr zugeordnet werden können.
- Sichern Sie das stehen auf einem soliden Fundament zu und befestigen Sie die Feder auf dem Stand. Stellen Sie sicher, dass genügend Platz unter die Feder zu dehnen, ohne auf den Tisch oder Boden vorhanden ist.
- Für jede der Massen, berechnen die Kraft auf die Feder ausgeübt durch die Erdanziehungskraft (F = mg). Beginnen Sie mit den wenigsten-massive Gewicht. Notieren Sie diese Werte in Tabelle 1.
- Messen Sie, wie hoch über der Oberfläche des Tisches der Frühling in seiner UN-gestreckten Position ist.
- Im Frühjahr das Mindeste-massive Gewicht beimessen und messen die Verschiebung Δy1 (siehe Abbildung 1). Notieren Sie diese Verschiebung in Tabelle 1.
- Erhöhen Sie mit dem Gewicht leicht das Gewicht vor der Freigabe. Die oszillierende Bewegung zu beobachten. Messen Sie die Periodendauer T mit einer Stoppuhr. Notieren Sie für eine genauere Messung die Zeit für mehrere Perioden und teilen Sie diese Zeit durch die Anzahl der Perioden beobachtet. Diese mehrfach zu tun und nehmen Sie die durchschnittliche Zeit für die Periode T in Tabelle 1gemessen.
- Wiederholen Sie die Schritte 1,5-1,6 für alle die Massen in der Reihenfolge ihrer Masse.
- Berechnen Sie die potentielle Energie der Feder für jede der verschiedenen Massen zu und zeichnen Sie diese in Tabelle 1.
- Zeichnen Sie die Kraft F als Funktion der Verdrängung Δy. Dies sollte nach Gleichung 1linear. Passen Sie eine Neigung in die Zeile. Diese Neigung entspricht der Frühling Konstante k. vergleichen Sie den Messwert auf der bekannten Wert der Feder.
- Mit dem bekannten Federkonstante und Gleichung 5, berechnen Sie, was die Periodendauer T der Schwingung für jeden der Massen sein sollte; Berichten sie in Tabelle 1. Vergleichen sie mit dem T, die mit der Stoppuhr im Schritt 1.6 gemessen wurde.
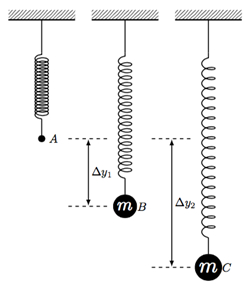
Abbildung 1: Srping Oszillation
Repräsentative Ergebnisse des Experiments, durchgeführt mit einem Frühling Konstante k = 10 N/m, sind in Tabelle 1dargestellt. Die Handlung des F gegen die Verdrängung Δy ist unten in Abbildung 2dargestellt. Die lineare Funktion ist mit einer Linie, und die Steigung der geraden ist die Federkonstante innerhalb einer Fehlerspanne gleich. Die Linearität des Ergebnisses zeigt die Gültigkeit von Hookes Gesetz (Gleichung 1).
Inspizieren Sie Tabelle 1 um zu sehen, wie die Periodendauer T der Schwingung auf die Masse bezieht, die mit der Feder verbunden ist. Je schwerer wird die Masse angebracht zu den Quellen, je länger der Zeitraum sein, wie es ist proportional zur Quadratwurzel der Masse (Gleichung 5). Beachten Sie, dass wenn eine größere Masse am Ende der Feder befestigt ist, die Feder weiter gedehnt werden. Die potentielle Energie des Systems ist größer, da sie eine Funktion der quadrierten Verschiebung vom Gleichgewicht (Gleichung 7) ist. Es ist sinnvoll, dass der Zeitraum länger dauern, bis eine größere Masse – denn die Feder weiter von Gleichgewicht verschoben, es dauert länger, die längere Strecke zurücklegen.
Tabelle 1. Ergebnisse.
| Masse (kg) | Gewicht / F (N) | Δy (m) | PE (J) | T gemessen (s) | T berechnet (s) |
| 0,5 | 4.9 | 0.49 | 2.4 | 1.3 | 1.4 |
| 0,75 | 7.4 | 0,74 | 5.4 | 1.6 | 1.7 |
| 1 | 9.8 | 0,98 | 9.6 | 1.9 | 1.9 |
| 1.5 | 14.7 | 1.5 | 21,6 | 2.5 | 2.4 |
| 2 | 19.6 | 2 | 38,4 | 2.9 | 2.8 |
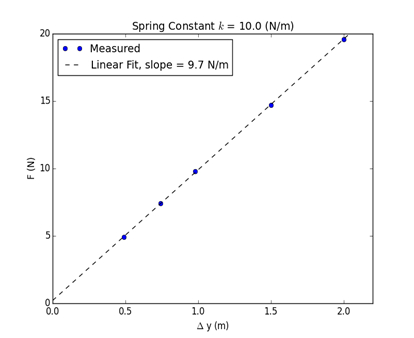
Abbildung 2: Grundstück von aufgebrachten Kraft (N) gegen Verschiebung.
Die Verwendung von Federn ist in unserem Alltag allgegenwärtig. Die Aussetzung von modernen Autos besteht aus Federn, die richtig gedämpft werden. Dies erfordert Kenntnisse über die Federkonstanten. Für glattere Cadillac Fahrten Federn mit einer niedrigeren Federkonstante verwendet, und die Fahrt ist "mushier." High-Performance-Autos verwenden Federn mit einer höheren Federkonstante zur besseren Handhabung. Sprungbretter sind auch gemacht, mit verschiedenen Federkonstanten, je nachdem, wie viel "bounce" gewünscht werden, wenn Sie vom Brett zu tauchen. Rock Kletterseilen sind auch leicht elastisch, so fällt ein Kletterer beim Klettern, das Seil wird nicht nur retten von auf den Boden, sondern es wird auch der Herbst mit seiner Elastizität dämpfen. Je kleiner die Federkonstante der Kletterseil, desto mehr ähnelt es Bungee-jumping.
In dieser Studie wurde die Verschiebung einer Feder, die aus der Anwendung der Kräfte der unterschiedlichen Größen gemessen. Die Gültigkeit von Hooke Gesetz wurde vom Plotten der daraus resultierenden Verschiebungen in Abhängigkeit von der Kraft, die auf die hängende Feder verifiziert. Oszillierende Bewegung wurde auch beobachtet, mit Perioden proportional zur Quadratwurzel der Masse an der Feder befestigt.
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Hookesches Gesetz und harmonische Schwingungen
Physics I
61.3K Ansichten

Newtonsche Gesetze der Bewegung
Physics I
75.7K Ansichten

Kraft und Beschleunigung
Physics I
79.1K Ansichten

Vektoren in mehrere Richtungen
Physics I
182.3K Ansichten

Kinematik und Projektilbewegung
Physics I
72.6K Ansichten

Newtonsches Gravitationsgesetz
Physics I
190.8K Ansichten

Der Impulserhaltung
Physics I
43.3K Ansichten

Reibung
Physics I
52.9K Ansichten

Gleichgewichts- und Freikörper-Diagramme
Physics I
37.3K Ansichten

Drehmoment
Physics I
24.3K Ansichten

Rotationsträgheit
Physics I
43.5K Ansichten

Drehimpuls
Physics I
36.2K Ansichten

Energie und Arbeit
Physics I
49.7K Ansichten

Enthalpie
Physics I
60.4K Ansichten

Entropie
Physics I
17.6K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten