Conservazione del momento angolare

Fonte: Nicholas Timmons, Asantha Cooray, PhD, Dipartimento di Fisica e Astronomia, Scuola di Scienze Fisiche, Università della California, Irvine, CA

L'obiettivo di questo esperimento è quello di testare il concetto di conservazione della quantità di moto. Impostando una superficie con pochissimo attrito, è possibile studiare le collisioni tra oggetti in movimento, incluso il loro momento iniziale e finale.

La conservazione della quantità di moto è una delle leggi più importanti della fisica. Quando qualcosa è conservato in fisica, il valore iniziale è uguale al valore finale. Per la quantità di moto, ciò significa che la quantità di moto iniziale totale di un sistema sarà uguale alla quantità di moto finale totale. La seconda legge di Newton afferma che la forza su un oggetto sarà uguale al cambiamento della quantità di moto dell'oggetto con il tempo. Questo fatto, combinato con l'idea che lo slancio è conservato, è alla base del funzionamento della meccanica classica ed è un potente strumento di risoluzione dei problemi.

La quantità di moto è definita come la massa di un oggetto volte la sua velocità :

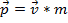. (Equazione 1)

Si può anche definire la quantità di moto in termini di forze che agiscono su un oggetto (seconda legge di Newton):

. (Equazione 2)

Ecco, 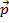è il momento iniziale ed è il momento finale, con la stessa convenzione usata per il tempo e . La somma delle forze che agiscono su un oggetto è uguale al cambiamento della quantità di moto dell'oggetto con il tempo. Pertanto, se non c'è forza netta che agisce su un oggetto, il cambiamento nella quantità di moto sarà zero. Detto in un altro modo, in un sistema chiuso senza forze esterne, lo slancio iniziale sarà uguale allo slancio finale.

Questo concetto è più facilmente comprensibile nel contesto delle collisioni unidimensionali e bidimensionali. Nelle collisioni unidimensionali, un oggetto con massa e velocità iniziale si scontra con un altro oggetto con massa e velocità iniziale 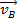. In queste collisioni, si presume che le forze esterne siano troppo piccole per avere un effetto. In laboratorio, una pista d'aria viene utilizzata per ridurre la quantità di attrito, una forza esterna, sugli alianti. Se il momentum iniziale è uguale al momentum finale, allora:

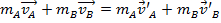, (Equazione 3)

dove le velocità innescate rappresentano le velocità finali e le velocità non innescate rappresentano le velocità iniziali.

Figura 1. Configurazione sperimentale.

1. Comprendere il timer photogate.

1. Utilizzando un bilanciamento, misura e registra la massa di ciascun aliante.
2. Posiziona un aliante sulla pista con un timer photogate.
3. Impostare il timer photogate sull'impostazione "gate".
4. Quando l'aliante passa attraverso il photogate, registrerà l'ora in cui la bandiera sopra l'aliante passa attraverso il cancello. Durante un viaggio di ritorno, il photogate non visualizzerà un nuovo orario. Cambia l'interruttore su "leggi" in modo che visualizzi l'ora iniziale più il tempo del secondo passaggio attraverso il cancello.
5. La bandiera è lunga 10 cm; determinare la velocità dell'aliante usando il fatto che la velocità è la distanza divisa per il tempo.
6. Invia l'aliante attraverso il photogate più volte, compresi i viaggi di ritorno dopo che è rimbalzato sulla parete più lontana, e misura le velocità per familiarizzare con l'attrezzatura. Ricorda che la velocità ha una direzione. Lascia che la direzione della velocità iniziale rappresenti positiva e la direzione opposta rappresenti i valori di velocità negativi.

2. Due alianti di uguale massa.

1. Posizionare due alianti e due timer photogate sulla pista, come nella Figura 1.
2. Utilizzate l'equazione 3 per determinare l'espressione per le velocità finali. In questa parte dell'esperimento, l'aliante B partirà dal riposo.
3. Dare all'aliante A una certa velocità iniziale in modo che si scontri con l'aliante B. Registrare la velocità iniziale dell'aliante A, così come le velocità finali di ciascun aliante. Fallo tre volte, registra i tuoi risultati e confrontali con la previsione teorica.

3. Due alianti di massa disuguale.

1. Aggiungi 4 pesi all'aliante B, che raddoppierà la sua massa. Ripetere i passaggi 2.1-2.3.

4. Masse uguali che non partono dal riposo

1. Rimuovere i pesi dall'aliante B.
2. Ripeti i passaggi 2.1-2.3, ma dai anche all'aliante B una velocità iniziale, nella direzione dell'aliante A.

Tabella 1. Risultati di due alianti di uguale massa.

Aliante (prova)	(cm/s)	(cm/s)	(cm/s)	(cm/s)	Differenza (%)
A (1)	72.5	-0.2	-	-	-
B (1)	0.0	67.1	72.5	66.9	8
A (2)	35.6	0.3	-	-	-
B (2)	0.0	37.4	35.6	37.7	6
A (3)	47.4	0.0	-	-	-
B (3)	0.0	47.8	47.4	47.8	1

Tabella 2. Risultati di due alianti di massa disuguale.

Aliante (prova)	(cm/s)	(cm/s)	(kg cm/s)	(kg cm/s)	Differenza (%)
A (1)	52.9	-10.7	-	-	-
B (1)	0.0	37.7	52.9	64.7	22
A (2)	60.2	-13.2	-	-	-
B (2)	0.0	41.5	60.2	69.8	16
A (3)	66.2	-12.0	-	-	-
B (3)	0.0	45.9	66.2	79.7	20

Tabella 3. Risultati da masse uguali che non partono dal riposo.

Aliante (prova)	(cm/s)	(cm/s)	(cm/s)	(cm/s)	Differenza (%)
A (1)	48.8	-29.9	-	-	-
B (1)	-42.4	39.8	6.4	9.9	55
A (2)	38.6	-25.2	-	-	-
B (2)	-33.4	32.8	5.2	7.6	46
A (3)	38.9	-43.1	-	-	-
B (3)	-48.5	36.3	-9.6	-6.8	41

I risultati dei passaggi 2, 3 e 4 confermano le previsioni fatte dall'equazione 3. Nel passaggio 2, l'aliante A si ferma quasi completamente dopo essersi scontrato con l'aliante B. Pertanto, quasi tutto il suo slancio viene trasferito all'aliante B. Nel passaggio 3, l'aliante A non si ferma dopo essersi scontrato con l'aliante più pesante B. Invece, ritorna nella direzione opposta dopo aver impartito un po 'di slancio all'aliante B. Nella fase 4, la quantità di moto totale del sistema rimane la stessa, nonostante i cambi di direzione di entrambi gli alianti. Il fatto che, in alcuni casi, la quantità di moto totale sembra aumentare e le velocità di entrambi gli alianti diminuiscono è legato al fatto che c'è un errore sperimentale e le collisioni stesse non sono completamente elastiche. Il suono e il calore eseferiti dalle collisioni possono togliere energia al sistema. Il fatto che la pista d'aria potrebbe non essere totalmente pianeggiante può cambiare il comportamento delle velocità degli alianti. Se la pista è anche leggermente inclinata, le velocità aumenteranno in quella direzione a causa della gravità. I risultati mostrano ancora che la quantità di moto totale del sistema, indipendentemente dalle velocità iniziali, rimane costante.

Senza la conservazione dello slancio, i razzi non lascerebbero mai il terreno. I razzi in realtà non spingono contro nulla: si basano sulla spinta per decollare. Inizialmente, il carburante di un razzo e il razzo stesso sono immobili e hanno zero slancio. Durante il lancio, il razzo spinge il combustibile esaurito molto rapidamente. Questo combustibile esaurito ha massa e slancio. Se la quantità di moto finale deve essere uguale alla quantità di moto iniziale (zero), allora ci deve essere una certa quantità di moto nella direzione opposta del combustibile scartato. Pertanto, il razzo viene spinto verso l'alto.

Chiunque abbia mai sparato con una pistola capisce la conservazione dello slancio. Come il sistema razzo/carburante dall'alto, anche il sistema pistola/munizioni inizia a riposo. Quando le munizioni vengono sparate fuori dalla pistola a una velocità tremenda, ci deve essere un certo slancio nella direzione opposta per annullare lo slancio del proiettile che accelera. Questo è noto come rinculo e può essere molto potente.

Il popolare ornamento da scrivania che consiste in diverse sfere di metallo appese alle corde è chiamato "culla di Newton" per una buona ragione. È un altro esempio di conservazione della quantità di moto. Quando una palla viene sollevata e rilasciata, colpisce il suo vicino, trasferendo il suo slancio. Lo slancio viaggia lungo la linea fino a quando la palla finale ha lo slancio della prima, facendola oscillare verso l'esterno. Questo andrebbe avanti per sempre se non fosse per le forze esterne, come la resistenza dell'aria e la perdita di energia dovuta alle collisioni.

In questo esperimento, la legge di conservazione della quantità di moto è stata verificata considerando la collisione di due alianti su una pista quasi senza attrito. Questa legge fondamentale è forse la più importante per il suo potere di risolvere i problemi. Se qualcuno conosce il momento iniziale, allora conosce il momento finale e viceversa.