Legge di Hooke e moto armonico semplice

Fonte: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Dipartimento di Fisica e Astronomia, Scuola di Scienze Fisiche, Università della California, Irvine, CA

L'energia potenziale è un concetto importante in fisica. L'energia potenziale è l'energia associata alle forze che dipendono dalla posizione di un oggetto rispetto all'ambiente circostante. L'energia potenziale gravitazionale, che viene discussa in un altro video, è l'energia associata che è direttamente proporzionale all'altezza di un oggetto dal suolo. Allo stesso modo, è possibile definire l'energia potenziale della molla, che è direttamente proporzionale allo spostamento di una molla dal suo stato rilassato. Una molla allungata o compressa ha energia potenziale, in quanto ha la capacità di lavorare su un oggetto. La "capacità di fare lavoro" è spesso citata come la definizione fondamentale di energia.

Questo video dimostrerà l'energia potenziale immagazzinata nelle molle. Verificherà anche l'equazione della forza di ripristino delle molle, o la legge di Hooke. La costante della molla è diversa per le molle di diverse elasticità. Verrà verificata la legge di Hooke e misurata la costante della molla attaccando pesi variabili a una molla sospesa e misurando gli spostamenti risultanti.

Tenere una molla nella sua posizione compressa o allungata richiede che qualcuno o qualcosa eserciti una forza sulla molla. Questa forza è direttamente proporzionale allo spostamento, Δy, della molla. A sua volta, la molla eserciterà una forza uguale e opposta:

F = -k Δy, (Equazione 1)

dove k è chiamato "costante di rigidità della molla". Questo è spesso indicato come una "forza di ripristino" perché la molla esercita una forza nella direzione opposta allo spostamento, indicato dal segno negativo. L'equazione 1 è nota come legge di Hooke.

Il semplice moto armonico si verificherà ogni volta che c'è una forza di ripristino proporzionale allo spostamento dall'equilibrio, come è nella legge di Hooke. Dalla seconda legge di Newton, F = ma, e riconoscendo che l'accelerazione a è la derivata seconda dello spostamento rispetto al tempo, l'equazione 1 può essere riscritta come:

m (d²y/dt²) = -k y. (Equazione 2)

La soluzione a questo differenziale di secondo ordine è ben nota per essere:

y(t) = Un peccato(ωt + φ), (Equazione 3)

dove A è l'ampiezza dell'oscillazione, ω = (k/m)^1/2, e l'angolo di fase φ dipende dalle condizioni iniziali del sistema. Le equazioni sotto forma di equazione 3 descrivono ciò che viene chiamato semplice moto armonico. Il periodo T, la frequenza fe la costante ω sono correlati da:

ω = 2πf = 2π/T. (Equazione 4)

Pertanto, il periodo T è dato da:

T = 2π (m/k)^1/2. (Equazione 5)

Si noti che T non dipende dall'ampiezza A dell'oscillazione. Pertanto, se un peso è appeso a una molla sospesa dalla verticale, il periodo di oscillazione risultante sarebbe proporzionale alla radice quadrata del peso attaccato.

Il lavoro necessario per allungare la molla a distanza y è W = <F> y, dove <F> è la forza media richiesta per allungare la corda. Poiché F è lineare in y, la media è solo la forza all'equilibrio (= 0) e la forza a y:

<F> = 1/2 [0 + ky]. (Equazione 6)

Il lavoro svolto e quindi l'energia potenziale elastica, PE, può essere scritta come:

PE = 1/2 k y². (Equazione 7)

L'energia potenziale di una molla sarà misurata in questo laboratorio.

1. Misurare la costante della molla e l'energia potenziale di una molla e confermare la relazione tra la massa e il periodo oscillatorio T.

1. Ottenere una molla con una costante di molla nota, un supporto a cui fissare la molla, almeno 5 pesi di varie masse che possono essere attaccati alla molla, un bastone metro e un cronometro.
2. Fissare il supporto a una solida base e fissare la molla al supporto. Assicurati che ci sia abbastanza spazio sotto la molla perché si allunghi senza colpire il tavolo o il terreno.
3. Per ciascuna delle masse, calcolare la forza esercitata sulla molla dalla forza gravitazionale terrestre (F = mg). Inizia con il peso meno massiccio. Registrare questi valori nella Tabella 1.
4. Misurare quanto è alta sopra la superficie del tavolo la molla mentre si trova nella sua posizione non tesa.
5. Fissare il peso meno massiccio alla molla e misurare lo spostamento Δy1 (vedere Figura 1). Registrare questo spostamento nella Tabella 1.
6. Con il peso attaccato, aumentare leggermente il peso prima di rilasciarlo. Osserva il movimento oscillatorio. Misurare il periodo T con un cronometro. Per una misurazione più accurata, registrare il tempo per più periodi e dividere quel tempo per il numero di periodi osservati. Fallo più volte e registra il tempo medio misurato per il periodo T nella Tabella 1.
7. Ripeti i passaggi 1,5-1,6 per tutte le masse, in ordine di massa crescente.
8. Calcola l'energia potenziale della molla per ciascuna delle diverse masse e registrale nella Tabella 1.
9. Traccia la forza F in funzione dello spostamento Δy. Secondo l'equazione 1, questo dovrebbe essere lineare. Adatta una pendenza alla linea. Questa pendenza corrisponderà alla costante di molla k. Confrontare il valore misurato con il valore noto della molla.
10. Usando la costante di molla nota e l'equazione 5, calcola quale dovrebbe essere il periodo T di oscillazione per ciascuna delle masse; segnalarli nella tabella 1. Confrontali con la T che è stata misurata con un cronometro nel passaggio 1.6.

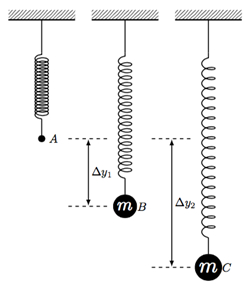
Figura 1: Oscillazione di Srping,

I risultati rappresentativi dell'esperimento, condotto con una molla di costante k = 10 N/m, sono mostrati nella Tabella 1. Il grafico di F rispetto allo spostamento Δy è tracciato di seguito nella Figura 2. La funzione lineare è adatta a una linea e la pendenza della linea è uguale alla costante della molla, entro un margine di errore. La linearità del risultato mostra la validità della legge di Hooke (Equazione 1).

Ispezionare la Tabella 1 per vedere come il periodo T di oscillazione è correlato alla massa che è attaccata alla molla. Più pesante è la massa attaccata alla molla, più lungo sarà il periodo, in quanto proporzionale alla radice quadrata della massa (Equazione 5). Inoltre, si noti che quando una massa più grande è attaccata alla fine della molla, la molla verrà allungata ulteriormente. L'energia potenziale del sistema è maggiore, in quanto è una funzione dello spostamento al quadrato dall'equilibrio (Equazione 7). Ha senso che il periodo sia più lungo per una massa più grande: poiché la molla è spostata ulteriormente dall'equilibrio, ci vorrà più tempo per percorrere quella distanza più lunga.
Tabella 1. Risultati.

Massa (kg)	Peso / F (N)	Δy (m)	PE (J)	T misurato (s)	T calcolato (s)
0.5	4.9	0.49	2.4	1.3	1.4
0.75	7.4	0.74	5.4	1.6	1.7
1	9.8	0.98	9.6	1.9	1.9
1.5	14.7	1.5	21.6	2.5	2.4
2	19.6	2	38.4	2.9	2.8

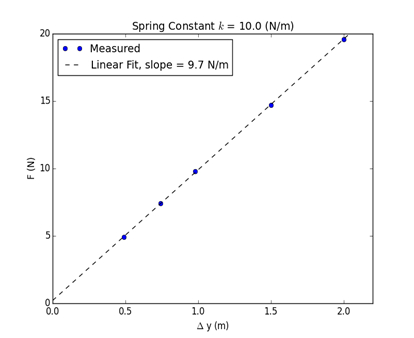
Figura 2: Grafico della forza applicata (N) rispetto allo spostamento.

L'uso delle molle è onnipresente nella nostra vita quotidiana. La sospensione delle auto moderne è realizzata con molle adeguatamente smorzate. Ciò richiede la conoscenza delle costanti di primavera. Per le corse Cadillac più fluide, vengono utilizzate molle con una costante di molla inferiore e la corsa è "mushier". Le auto ad alte prestazioni utilizzano molle con una costante di molla più elevata per una migliore maneggevolezza. I trampolini sono anche realizzati con molle di diverse costanti primaverili, a seconda di quanto "rimbalzo" si desidera quando ci si immerge dalla tavola. Le corde per arrampicata su roccia sono anche leggermente elastiche, quindi se uno scalatore cade durante l'arrampicata, la corda non solo la salverà dal colpire il terreno, ma smorzerà anche la caduta con la sua elasticità. Più piccola è la costante primaverile di una corda da arrampicata, più assomiglia al bungee jumping.

In questo studio, è stato misurato lo spostamento di una molla risultante dall'applicazione di forze di varia grandezza. La validità della legge di Hooke è stata verificata tracciando gli spostamenti risultanti in funzione della forza esercitata sulla molla sospesa. È stato osservato anche un movimento oscillatorio, con periodi proporzionali alla radice quadrata della massa attaccata alla molla.