Momento angolare
Panoramica
Fonte: Nicholas Timmons, Asantha Cooray, PhD, Dipartimento di Fisica e Astronomia, Scuola di Scienze Fisiche, Università della California, Irvine, CA
Il momento angolare è definito come il prodotto del momento di inerzia e della velocità angolare dell'oggetto. Come il suo analogo lineare, il momento angolare è conservato, il che significa che il momento angolare totale di un sistema non cambierà se non ci sono coppie esterne sul sistema. Una coppia è l'equivalente rotazionale di una forza. Poiché è un momento angolare conservato, è una quantità importante in fisica.
L'obiettivo di questo esperimento è misurare il momento angolare di un'asta rotante e utilizzare la conservazione del momento angolare per spiegare due dimostrazioni rotazionali.
Principi
Il momento angolare può essere scritto come:
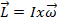 , (Equazione 1)
, (Equazione 1)
dove 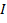 è il momento di inerzia e è la
è il momento di inerzia e è la  velocità angolare. Il momento di inerzia è l'analogo rotazionale della massa per il moto lineare. È correlato alla distribuzione di massa di un oggetto rotante e all'asse di rotazione. Maggiore è il momento di inerzia, maggiore è la coppia necessaria per causare un'accelerazione angolare su un oggetto. La regola della mano destra può essere utilizzata per determinare la direzione del momento angolare. Quando le dita della mano destra si arricciano nella direzione di rotazione, il pollice esteso punta nella direzione del momento angolare.
velocità angolare. Il momento di inerzia è l'analogo rotazionale della massa per il moto lineare. È correlato alla distribuzione di massa di un oggetto rotante e all'asse di rotazione. Maggiore è il momento di inerzia, maggiore è la coppia necessaria per causare un'accelerazione angolare su un oggetto. La regola della mano destra può essere utilizzata per determinare la direzione del momento angolare. Quando le dita della mano destra si arricciano nella direzione di rotazione, il pollice esteso punta nella direzione del momento angolare.
Una coppia è definita come il prodotto di una forza applicata a una certa distanza da un asse di rotazione:
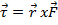 , (Equazione 2)
, (Equazione 2)
dove 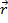 è la distanza dall'asse di rotazione e
è la distanza dall'asse di rotazione e 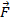 è la forza applicata. Se una coppia agisce su un oggetto, la velocità angolare di quell'oggetto cambierà, insieme al suo momento angolare. Se la somma delle coppie su un oggetto è uguale a zero, il momento angolare totale sarà conservato e avrà lo stesso valore finale di inizialmente.
è la forza applicata. Se una coppia agisce su un oggetto, la velocità angolare di quell'oggetto cambierà, insieme al suo momento angolare. Se la somma delle coppie su un oggetto è uguale a zero, il momento angolare totale sarà conservato e avrà lo stesso valore finale di inizialmente.
Un divertente esempio di conservazione del momento angolare può essere dimostrato con una ruota da bici e una sedia rotante. La ruota e la persona sulla sedia costituiscono un sistema con un certo momento angolare. Se la persona applica una coppia per far girare la ruota, con l'asse che punta verticalmente, il sistema avrà guadagnato momento angolare. Se poi la persona capovolge la ruota che gira, inizierà a girare sulla sua sedia nella direzione opposta alla ruota che gira. Qui, il sistema aveva un momento angolare, con la sua direzione determinata dalla regola della mano destra. Quando la ruota è stata capovolta, il momento angolare del sistema ha cambiato direzione. A causa della conservazione, la sedia ha iniziato a ruotare nella direzione opposta in modo che il momento angolare totale del sistema fosse uguale a quello del sistema prima che la ruota fosse capovolta.
Un'altra dimostrazione della conservazione del momento angolare può essere fatta con una sedia rotante e due pesi. Se i pesi sono tenuti a distanza di braccio mentre la sedia sta girando e poi vengono portati vicino al petto, ci sarà un aumento della velocità angolare. Questo accade perché avvicinando i pesi all'asse di rotazione diminuisce il momento di inerzia del sistema. Se non c'è più forza che agisce per far girare la sedia, allora la coppia sul sistema è zero. Il momento angolare deve rimanere costante, poiché non ci sono coppie, e l'unico modo per farlo è che la velocità angolare aumenti.
In questo esperimento, un'asta rotante è collegata a un peso che cade. Il peso in caduta fornirà una coppia sull'asta e il momento angolare sarà misurato in due punti: prima quando il peso è sceso a metà strada e poi di nuovo una volta che il peso raggiunge la fine della corda. Vedere la Figura 1 per un'immagine della configurazione sperimentale.
Il momento di inerzia di una canna da spinning è 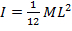 , dove è la massa
, dove è la massa 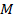 dell'asta e
dell'asta e 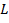 è la lunghezza. Queste quantità possono essere misurate prima che l'esperimento abbia luogo. Per trovare la velocità
è la lunghezza. Queste quantità possono essere misurate prima che l'esperimento abbia luogo. Per trovare la velocità  angolare, verranno utilizzate le equazioni cinematiche rotazionali:
angolare, verranno utilizzate le equazioni cinematiche rotazionali:
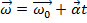 . (Equazione 3)
. (Equazione 3)
L'equazione 3 afferma che la velocità angolare finale  è uguale alla velocità angolare iniziale
è uguale alla velocità angolare iniziale  più l'accelerazione angolare
più l'accelerazione angolare 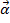 , moltiplicata per il tempo. Perché l'asta inizierà a
, moltiplicata per il tempo. Perché l'asta inizierà a  riposo, sarà uguale a zero. L'accelerazione angolare
riposo, sarà uguale a zero. L'accelerazione angolare 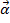 è definita da
è definita da 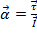 , dove è la coppia e è il momento di
, dove è la coppia e è il momento di 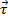
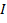 inerzia. La coppia è il prodotto incrociato della distanza dall'asse di rotazione alla forza e della forza del peso che causa una tensione nella corda, che fa ruotare l'asta:
inerzia. La coppia è il prodotto incrociato della distanza dall'asse di rotazione alla forza e della forza del peso che causa una tensione nella corda, che fa ruotare l'asta: 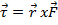 . Quella forza che agisce sulla puleggia è uguale alla forza sul peso:
. Quella forza che agisce sulla puleggia è uguale alla forza sul peso: 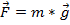 , dove è la massa e è
, dove è la massa e è 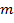
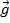 l'accelerazione dovuta alla gravità. Il raggio
l'accelerazione dovuta alla gravità. Il raggio 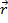 della coppia sarà la distanza dalla corda avvolta all'asse di rotazione.
della coppia sarà la distanza dalla corda avvolta all'asse di rotazione.

Figura 1. Configurazione sperimentale. Inserto: 1) supporto ad anello grande, 2) estensore, 3) assemblaggio rotante, 4) peso e 5) barra di coppia.
Procedura
1. Testare la teoria della conservazione del momento angolare con la ruota della bici.
- Mentre sei seduto su una sedia che può ruotare liberamente, inizia a far girare la ruota della bici e poi tienila per le maniglie in modo che la sua direzione del momento angolare sia verticale.
- Mentre si tiene la ruota per le due maniglie, capovolgere la ruota in modo che il suo momento angolare punti nella direzione opposta. Nota come la sedia inizierà a ruotare.
2. Testare la teoria della conservazione del momento angolare con due pesi.
- Mentre sei seduto su una sedia che può ruotare liberamente, tieni due pesi a distanza di braccio.
- Fai girare la sedia a un partner e poi porta i pesi vicino al petto. Si noti l'aumento della velocità di rotazione della sedia.
3. Misurare il cambiamento del momento angolare nella canna da spinning.
- Misura la lunghezza dell'asta e la sua massa. Usando un metro stick, misurare il punto intermedio del peso in caduta e contrassegnare il raggio verticale con del nastro adesivo per avere un riferimento. Calcola il momento di inerzia dell'asta.
- Aggiungere 200 g alla fine della corda e avvolgerla verso l'alto. Prendi nota di dove si trova il punto intermedio della stringa.
- Rilascia il peso e misura la quantità di tempo necessaria per arrivare a metà strada e poi di nuovo in fondo. Fallo tre volte e prendi i valori medi. Calcola il momento angolare in entrambi i punti.
- Aumentare il peso alla fine della corda a 500 g e ripetere il passaggio 3.3.
- Aumentare il peso a 1.000 g e ripetere il passaggio 3.3.
Risultati
| Un sacco g) |
Momento angolare a metà strada (kg m2)/s |
Momento angolare in basso (kg m2)/s |
Differenza (kg m2)/s |
| 200 | 0.41 | 0.58 | 0.17 |
| 500 | 0.66 | 0.91 | 0.25 |
| 1,000 | 0.93 | 1.32 | 0.39 |
Nel primo passaggio, è stata confermata la teoria della conservazione del momento angolare, poiché la sedia ha iniziato a ruotare quando la ruota è stata capovolta. Nella seconda fase, la teoria della conservazione del momento angolare è stata nuovamente confermata, poiché la sedia ha iniziato a girare più velocemente quando i pesi sono stati portati e il momento di inerzia del sistema è stato ridotto. Nella terza fase del laboratorio, l'aumento della coppia sull'asta di filatura ha aumentato il momento angolare. Con tutte le altre quantità costanti, il momento angolare aumentava linearmente con il tempo.
Applicazione e Riepilogo
Proprio come nella parte della sedia rotante del laboratorio, cambiare il momento di inerzia di un oggetto può aumentare o diminuire la velocità angolare di quell'oggetto. I pattinatori di figura ne approfittano e a volte iniziano a girare con le braccia tese e poi portano le braccia vicino ai loro corpi, il che li farà girare molto più velocemente.
Perché è più facile stare in equilibrio su una bici quando è in movimento? La risposta è il momento angolare. Quando le ruote non girano, è facile che la bici cada. Una volta che le ruote sono in movimento, avranno una certa quantità di momento angolare. Più grande è il momento angolare, maggiore è la coppia necessaria per cambiarlo, quindi è più difficile ribaltare la moto.
Se un quarterback che gioca a calcio lancia senza mettere alcun giro sulla palla, il suo volo sarà traballante e potrebbe mancare il suo bersaglio. Per evitare questo, i quarterback usano le dita per far girare il pallone quando lo lanciano. Quando la palla ruota mentre vola attraverso l'aria, ha un momento angolare, che richiede la coppia per cambiare la direzione del momento angolare. La palla non oscillerà o girerà in aria.
In questo esperimento, il concetto di conservazione della quantità di moto è stato testato in due dimostrazioni. In uno, la direzione del momento angolare è stata conservata, e nell'altro, la magnitudine è stata conservata. Nell'ultima parte dell'esperimento, è stato misurato l'effetto di una coppia sul momento angolare.
Vai a...
Video da questa raccolta:

Now Playing
Momento angolare
Physics I
36.6K Visualizzazioni

I principi della dinamica (leggi di Newton)
Physics I
76.9K Visualizzazioni

Forza e accelerazione
Physics I
79.6K Visualizzazioni

Vettori in più direzioni
Physics I
182.7K Visualizzazioni

Cinematica e moto parabolico
Physics I
73.1K Visualizzazioni

Legge di gravitazione universale di Newton
Physics I
192.7K Visualizzazioni

Conservazione del momento angolare
Physics I
43.6K Visualizzazioni

Attrito
Physics I
53.1K Visualizzazioni

Legge di Hooke e moto armonico semplice
Physics I
61.6K Visualizzazioni

Diagrammi di equilibrio e corpo libero
Physics I
37.6K Visualizzazioni

Momento meccanico
Physics I
26.2K Visualizzazioni

Momento di inerzia
Physics I
43.8K Visualizzazioni

Energia e lavoro
Physics I
50.4K Visualizzazioni

Entalpia
Physics I
60.6K Visualizzazioni

Entropia
Physics I
17.8K Visualizzazioni