Entropia

Fonte: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Dipartimento di Fisica e Astronomia, Scuola di Scienze Fisiche, Università della California, Irvine, CA

La seconda legge della termodinamica è una legge fondamentale della natura. Afferma che l'entropia di un sistema aumenta sempre nel tempo o rimane costante nei casi ideali in cui un sistema è in uno stato stazionario o sta subendo un "processo reversibile". Se il sistema sta subendo un processo irreversibile, l'entropia del sistema aumenterà sempre. Ciò significa che la variazione di entropia, ΔS, è sempre maggiore o uguale a zero. L'entropia di un sistema è una misura del numero di configurazioni microscopiche che il sistema può raggiungere. Ad esempio, il gas in un contenitore con volume, pressione e temperatura noti può avere un numero enorme di possibili configurazioni delle singole molecole di gas. Se il contenitore viene aperto, le molecole di gas fuoriescono e il numero di configurazioni aumenta drammaticamente, essenzialmente avvicinandosi all'infinito. Quando il contenitore viene aperto, si dice che l'entropia aumenti. Pertanto, l'entropia può essere considerata una misura del "disordine" di un sistema.

L'entropia è una "proprietà di stato", che è una quantità che dipende solo dallo stato corrente del sistema. Le quantità che sono proprietà di stato non dipendono dal percorso con cui il sistema è arrivato al suo stato attuale. Pertanto, il modo più utile per quantificare una proprietà statale è misurare il suo cambiamento.

La variazione dell'entropia S è definita come:

ΔS = Q / T, (Equazione 1)

dove Q è il calore fornito al sistema e T è la temperatura del sistema. Nel contesto della termodinamica, il calore, come il lavoro, è definito come un trasferimento di energia. Il calore è energia trasferita da un oggetto all'altro a causa di una differenza di temperatura. Considera un bagno di ghiaccio e acqua a 0 °C. Se si fornisce calore al bagno di ghiaccio / acqua, parte del ghiaccio si scioglierà e il numero di stati disponibili per le molecole d'acqua aumenterà di una grande quantità, proporzionale alla quantità di calore che è stata aggiunta al sistema. L'entropia aumenterà quindi proporzionalmente a questa quantità. La relazione tra due oggetti a temperature diverse fu descritta per la prima volta da Newton.

La legge di Newton del raffreddamento afferma che il tasso di variazione della temperatura di qualche oggetto è proporzionale alla differenza tra la propria temperatura e la temperatura dell'ambiente circostante. Per un oggetto a temperatura T posto in un sistema chiuso alla temperatura T_f, questa variazione di temperatura in funzione del tempo t è descritta dall'equazione differenziale:

dT/dt = -k(T - T_f ), (Equazione 2)

dove k è una costante che dipende dalle caratteristiche dell'oggetto e dell'ambiente circostante. L'equazione 1 è scritta in modo equivalente come:

-k dt = dT / (T - T_f ). (Equazione 3)

L'integrazione di entrambi i lati dà:

-k t = log(T - T_f ) + log C. (Equazione 4)

Applicando la funzione esponenziale a entrambi i lati dell'equazione e quindi riorganizzando si ottiene:

T - T_f = C e^-kt . (Equazione 5)

Se l'oggetto in questione si trova ad una temperatura iniziale T_i al tempo t = 0:

T_i- T_f = C. (Equazione 6)

Ne consegue che la temperatura in funzione del tempo è:

T(t) =T_f + (T_i- T_f ) e^-kt . (Equazione 7)

Pertanto, quando un oggetto caldo viene collocato in un sistema chiuso più freddo, la sua temperatura diminuirà a un ritmo esponenziale. In questo sistema chiuso, il calore dell'oggetto caldo Q aumenterà la temperatura dell'ambiente più fresco e quindi aumenterà il numero di stati disponibili. Quindi, il cambiamento di entropia, ΔS, è positivo e diverso da zero.

1. Installazione.

1. Procuratevi un elemento riscaldante e un supporto, un termometro, un cronometro, alcuni asciugamani di carta, acqua e un grande becher.
2. Riempire il becher con acqua sufficiente in modo che il campione non si raffreddi troppo rapidamente(cioè almeno 500 ml).
3. Posizionare il becher pieno d'acqua sul supporto sotto l'elemento riscaldante e accenderlo.
4. Una volta che il becher d'acqua raggiunge l'ebollizione, inserire il termometro e spegnere l'elemento riscaldante.
5. Rimuovere con cura il becher dal supporto di riscaldamento e posizionarlo sul tavolo, sopra gli asciugamani di carta. Questi agiranno come isolamento dal tavolo.

2. Registrazione dei dati.

1. Avvia il cronometro e registra la temperatura e l'ora.
2. Per i primi 20 minuti, fai una misurazione circa ogni 1 minuto.
3. Per i prossimi 20 minuti, fai una misurazione circa ogni 3-5 minuti.
4. Registrare questi valori nella Tabella 1.
5. Tracciare i punti dati raccolti nella Tabella 1 in un grafico della temperatura rispetto al tempo.
6. Utilizzando la temperatura iniziale dell'acqua e due punti dati qualsiasi per il tempo e la temperatura, risolvere l'equazione 7 per la costante di raffreddamento k.
7. Usando questo valore per k, tracciate l'equazione 7 come una funzione continua di t. Confrontare la funzione con i punti dati raccolti.

I risultati rappresentativi per 680 ml di acqua sono riportati nella Tabella 1. La costante di raffreddamento k è stata trovata utilizzando i punti dati nella tabella e risolvendo l'equazione 7. Dopo 35 min, T(35) = 50,6. La temperatura iniziale era di 100 °C e la raccolta dei dati è cessata a 28,5 °C. Usando queste variabili si ottiene la seguente equazione per ottenere k:

50,6 = 28,5 + (100 - 28,5) e^{-k 35}. (Equazione 8)

Risolvendo per k si ottiene un valore k = 0,034. La curva con questa costante di raffreddamento è mostrata come una linea grigia tratteggiata nella Figura 1, insieme ai punti dati dell'esperimento. La forma funzionale dell'equazione 6 corrisponde molto da vicino ai risultati sperimentali.

Man mano che l'acqua si raffredda, l'entropia diminuisce, poiché il numero di stati disponibili per le molecole d'acqua diminuisce. L'entropia dell'aria ambiente nella stanza aumenta perché il becher d'acqua trasferisce calore alle molecole d'aria che lo circondano; l'entropia complessiva del sistema acqua + aria aumenta. Il numero di stati che le molecole d'aria ora più calde possono occupare è molto più alto rispetto a prima che l'acqua calda fosse introdotta nella stanza.

In forma differenziale, il calore dQ aggiunto o rimosso dall'acqua può essere calcolato utilizzando la relazione tra massa, calore specifico ce variazione di temperatura:

dQ = mc dT, (Equazione 9)

dove c è noto per essere 4,18 J/(gK) per l'acqua. Il cambiamento di entropia dell'acqua è quindi:

ΔS_acqua =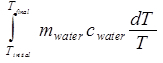

= m_acqua c_acqua ln(T_finale / T_iniziale). (Equazione 10)

Usando la conversione in Kelvin come K = °C + 273,15, la variazione dell'entropia dell'acqua viene calcolata come:

Acqua ΔS = 680 g * 4,18 J/(g K) * ln[(28,5 + 273,15)/(100 + 273,15)]

= -604 J/K.

La temperatura dell'aria ambiente è costante a 20,4 °C, quindi questo è un processo isotermico. Il cambiamento di entropia dell'aria è quindi:

ΔS_aria = ,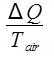

dove Q è il calore rilasciato dall'acqua, che è dato dall'equazione 9. La variazione di entropia dell'aria viene quindi calcolata come:

ΔS_aria =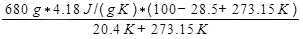

= 3337 J/K.

La variazione totale dell'entropia del sistema acqua + aria, ΔS_tot, è la somma dei singoli cambiamenti di entropia dell'acqua e dell'aria ambiente:

ΔS_tot = ΔS_acqua +ΔS_aria (Equazione 11)

= -604 J/k + 3337 J/K

= 2733 J/K.

Tabella 1. Temperature registrate durante l'esperimento.

Tempo (min s)	Temperatura dell'acqua (°C)
0 0	99.6
1 10	97.1
1 50	94.2
2 30	91.8
3 22	89
4 05	87.2
5 08	82.7
6 05	82.4
8 25	78
9 15	76.5
10 15	74.6
11 38	72.7
12 58	70.7
13 58	69.2
15 15	67.7
16 55	65.8
18 38	64
20 25	62.3
24 02	58.8
25 45	57.3
34 45	50.6
40 50	47.4
44 30	45.9
49 59	43.6
53 42	42.4
60 01	40.2
64 20	39.5
76 37	37
103 50	32.1
116 41	30.3
122 46	29.6
134 11	28.5

Figura 1. Grafico della temperatura rispetto al tempo. I punti blu indicano i dati sperimentali e la linea tratteggiata rappresenta i dati teorici basati sulla legge di raffreddamento di Newton.

Un paio di cuffie tenute in una borsa tende sempre ad annodarsi: questo è un aumento dell'entropia causato dal portare la borsa in giro. È necessario lavorare sulle cuffie per snodarle e diminuire l'entropia (questo può essere pensato come un "processo reversibile"). Il ciclo del motore termico più efficiente consentito dalle leggi fisiche è il ciclo di Carnot. La seconda legge afferma che non tutto il calore fornito a un motore termico può essere utilizzato per fare il lavoro. L'efficienza di Carnot imposta il valore limite sulla frazione di calore che può essere utilizzata. Il ciclo consiste in due processi isotermici seguiti da due processi adiabatici. Un frigorifero, che è essenzialmente solo una pompa di calore, è anche un classico esempio della seconda legge. I frigoriferi spostano il calore da una posizione a una temperatura più bassa (la "fonte") a un'altra posizione a una temperatura più elevata (il "dissipatore di calore") utilizzando il lavoro meccanico. Secondo la seconda legge, il calore non può fluire spontaneamente da un luogo più freddo a uno più caldo; pertanto, il lavoro (energia) è necessario per la refrigerazione.

La legge di Newton del raffreddamento è stata dimostrata da un becher pieno d'acqua a 100 °C che si raffredda a temperatura ambiente, il che ha portato ad un aumento dell'entropia del sistema acqua-aria. Misurando la temperatura dell'acqua in funzione del tempo per un periodo di 135 min, è stato possibile confermare che il raffreddamento dell'acqua era di forma esponenziale. La costante di raffreddamento del campione d'acqua è stata trovata risolvendo l'equazione di raffreddamento utilizzando i dati raccolti.