여러 방향의 벡터
Overview
출처: 니콜라스 티몬스, 아산타 쿠레이, 박사, 물리학 및 천문학학과, 물리 과학 학교, 캘리포니아 대학, 어바인, 캘리포니아
이 실험에서는 벡터가 여러 방향으로 추가하고 빼는 방법을 보여 줍니다. 목표는 여러 벡터의 추가 또는 뺄셈을 과질적으로 계산한 다음 실험적으로 계산을 확인하는 것입니다.
벡터는 크기와 방향을 모두 갖춘 개체입니다. 벡터의 크기는 단순히 길이로 표시되며 방향은 일반적으로 x-축으로만드는 각도로 정의됩니다. 힘은 벡터이므로 벡터의 물리적 표현으로 사용할 수 있습니다. 병력 시스템을 설정하고 힘 사이의 평형을 생성할 추가 병력을 찾아서 벡터 시스템을 실험적으로 검증할 수 있습니다.
Principles
도 1에서  벡터뿐만 아니라 x-축 및
벡터뿐만 아니라 x-축 및  x-축으로만드는 각도 θ를 나타낸다.
x-축으로만드는 각도 θ를 나타낸다.

그림 1.
두 개의 벡터를 추가하거나 빼려면 x 및 y-구성요소 측면에서 벡터를 설명하는 것이 유용합니다. x-구성요소는 수학적으로 다음과 같이 표현되는 x-방향으로가리키는 벡터의 양입니다.
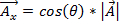 . (방정식 1)
. (방정식 1)
y-구성요소는 다음과 같이 표시됩니다.
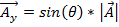 . (방정식 2)
. (방정식 2)
크기는  다음과 같이 정의됩니다.
다음과 같이 정의됩니다.
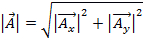 . (방정식 3)
. (방정식 3)
두 개의 벡터를 추가하거나 빼려면 벡터를 x 및 y-구성요소로 나누기만 한 다음 해당 구성 요소를 각각 추가하거나 빼기만 하면 됩니다.
예를 들어 벡터 및 벡터인 경우 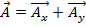 두
두 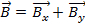 벡터를
벡터를  추가합니다.
추가합니다.
벡터가 x 축과관련하여 만드는 각도 θ를 확인하려면 다음 방정식을 사용합니다.
 . (방정식 4)
. (방정식 4)
벡터의 크기와 방향이 모두 있기 때문에 두 벡터를 곱하는 것은 두 숫자를 곱하는 것만큼 간단하지 않습니다. 벡터를 곱하는 방법에는 점 제품및 교차 제품이라는 두 가지 방법이 있습니다. 점 생성물은 또는 여기로 기록될 수 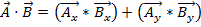
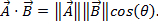 있으며, θ는 두 벡터 사이의 각도이다. 결과는 방향이 아니라 크기만 을 가지고 있습니다. 물리학에서 도트 생성물의 응용은 작업이 힘 시간거리로 정의되는 작업(W)이며, 여기서 두
있으며, θ는 두 벡터 사이의 각도이다. 결과는 방향이 아니라 크기만 을 가지고 있습니다. 물리학에서 도트 생성물의 응용은 작업이 힘 시간거리로 정의되는 작업(W)이며, 여기서 두 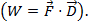 벡터의 교차 생성물은
벡터의 교차 생성물은 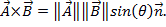 도트 생성물과 유사하지만, 크로스 제품은
도트 생성물과 유사하지만, 크로스 제품은  두 벡터에 수직인 크기 1을 가진 벡터로 정의된 용어를 포함하고
두 벡터에 수직인 크기 1을 가진 벡터로 정의된 용어를 포함하고 
 있다. 교차 제품의 결과는 벡터입니다. 물리학에서 교차 제품의 한 예는
있다. 교차 제품의 결과는 벡터입니다. 물리학에서 교차 제품의 한 예는  반경 힘 시간의 결과입니다 토크입니다
반경 힘 시간의 결과입니다 토크입니다 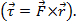
벡터는 중력이나 마찰과 같은 힘이 벡터로 표현될 수 있기 때문에 물리학에 유용합니다. 이 실험실에서 중력의 힘은 힘의 벡터 특성과 그 힘이 여러 방향으로 추가하는 방법을 시연하는 데 사용됩니다. 지구 표면의 중력은 다음과 같이 기록됩니다.
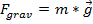 , (수학식 5)
, (수학식 5)
 물체의 질량은 어디에,
물체의 질량은 어디에,  지구 표면 근처의 중력의 가속은 (9.8 m/s2)이다.
지구 표면 근처의 중력의 가속은 (9.8 m/s2)이다.
Procedure
1. 밸런스 힘.
- 힘 테이블에는 반대 방향으로 향하는 동일한 질량으로 두 개의 풀리를 설정합니다(각도의 180° 차이).
- 각 힘의 힘은 와
 같습니다. 이동해서는 안 되는 힘 테이블중앙의 링을 검사하여 두 힘이 동등하고 반대인지 확인합니다.
같습니다. 이동해서는 안 되는 힘 테이블중앙의 링을 검사하여 두 힘이 동등하고 반대인지 확인합니다. - 이러한 힘과 연관된 벡터의 구성 요소가 추가되면 결과 벡터의 크기가 0입니다. 이것은 모든 힘이 평형에 있는지 확인하는 방법입니다.
2. 분석 계산.
- 이 실험실은 평형의 세 가지 힘으로 구성됩니다. 두 개의 힘이 알려지지만, 세 번째 힘은 벡터 이론을 사용하여 먼저 의도적으로 발견된 다음 실험적으로 발견될 것입니다. 이 랩의 경우
 기간 동안 0°로 유지하십시오.
기간 동안 0°로 유지하십시오. - 알고 있는 경우

 시스템에
시스템에  추가될 때 두 힘이 평형에 있는 경우, 그 다음
추가될 때 두 힘이 평형에 있는 경우, 그 다음  크기는 동일하지만 합계(+)와 반대 방향으로 발생합니다.
크기는 동일하지만 합계(+)와 반대 방향으로 발생합니다. 

- 및 의 크기를

 계산합니다.
계산합니다.  1 뉴턴(N)이 와 동일한 힘의 단위라는 사실을
1 뉴턴(N)이 와 동일한 힘의 단위라는 사실을  사용하십시오.
사용하십시오. - 벡터 이론을 사용하여
 합계(+)인 경우 크기를
합계(+)인 경우 크기를 
 계산합니다.
계산합니다. - 벡터 이론을 사용하여
 합계(+)인 경우 각도를
합계(+)인 경우 각도를 
 계산합니다.
계산합니다.
3. 실험.
- 표 1의 첫 번째 줄에 있는 값을 따라
 힘 테이블에 두 힘을
힘 테이블에 두 힘을  설정합니다. 0°에서 유지해야
설정합니다. 0°에서 유지해야  합니다.
합니다. - 세 번째 힘을
 설정, 무게를 추가하고 평형에 도달 할 때까지 각도를 변경하여. 표 2에서이러한 값을 기록합니다.
설정, 무게를 추가하고 평형에 도달 할 때까지 각도를 변경하여. 표 2에서이러한 값을 기록합니다. - 네 가지 경우 각각에 대해 3.2 단계를 반복합니다.
- 를 계산하여 분석 결과와 백분율 차이를
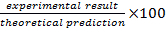 결정합니다. 이러한 계산된 값으로 표 2를 완료합니다.
결정합니다. 이러한 계산된 값으로 표 2를 완료합니다.
Results
랩의 결과는 표 1과 표 2에표시됩니다.
표 1. 설치.
| 설치 # | A | B | ||
| 미사 | 각 | 미사 | 각 | |
| 1 | 100 | 0 | 100 | 20 |
| 2 | 100 | 0 | 150 | 40 |
| 3 | 200 | 0 | 150 | 60 |
| 4 | 200 | 0 | 250 | 80 |
표 2. 분석 결과.
| 설치 # | 크기  (N) |
크기  (N) |
각  (°) |
크기  (N) |
각  (°) |
| 1 | 0.98 | 0.98 | 20 | 1.93 | 10 |
| 2 | 0.98 | 1.47 | 40 | 2.31 | 24 |
| 3 | 1.96 | 1.47 | 60 | 2.98 | 25 |
| 4 | 1.96 | 2.45 | 80 | 3.39 | 45 |
표 3. 실험 결과.
| 설치 # | 실험 적 크기  (N) |
분석 크기  (N) |
다름 (%) |
실험적 각도  (°) |
분석 각도 (°) |
다름 (%) |
| 1 | 2.1 | 1.93 | 9 | 11 | 10 | 10 |
| 2 | 2.2 | 2.31 | 5 | 26 | 24 | 8 |
| 3 | 2.8 | 2.98 | 6 | 28 | 25 | 12 |
| 4 | 3.5 | 3.39 | 3 | 43 | 45 | 5 |
실험 결과는 분석 계산과 일치합니다. 두 벡터의 합계와 둘 사이의 각도는 방정식 1-5를사용하여 계산할 수 있습니다. 방정식은 힘과 같은 물리적 벡터를 계산하는 데 유효합니다.
Application and Summary
야구의 외야수는 이동 중공을 잡기 위해 벡터를 이해해야 합니다. 외야수가 공의 속도만 알고 있다면, 그는 오른쪽이 아닌 왼쪽 필드로 달려가 공을 놓칠 수 있습니다. 그는 단지 히트의 방향을 알고 있다면, 그는 단지 그의 머리 를 통해 항해 공을 보고, 충전 할 수 있습니다. 그가 벡터를 이해한다면, 공이 부딪히자마자, 그는 공을 잡을 때 공이 어디에 될지 예측하기 위해 크기와 방향을 모두 고려할 수 있습니다.
비행기가 하늘에 있을 때 속도와 방향을 벡터로 기록할 수 있습니다. 바람이 부는 경우, 바람 벡터는 결과의 시스템 벡터를 제공하기 위해 평면의 벡터에 추가합니다. 예를 들어 비행기가 바람에 날아가는 경우 결과 벡터의 크기는 초기 크기보다 낮습니다. 이는 바람으로 향할 때 느리게 움직이는 평면에 해당하므로 직관적인 의미가 있습니다.
두 오브젝트가 충돌하여 함께 고정하면 최종 모멘텀(벡터)은 두 개의 초기 모멘텀 벡터의 합으로 근사할 수 있습니다. 이것은 실제 세계에서와 같이 충돌하는 두 물체가 충돌하는 경우와 같이 충돌에서 열이나 변형과 같은 추가 요소를 고려해야 합니다. 모멘텀은 속도를 곱한 물체의 질량일 뿐입니다. 서로 다른 방향으로 이동하는 얼음에 두 스케이터가 서로 충돌하고 서로 붙잡는 경우, 그들의 최종 방향과 속도는 초기 벡터 구성 요소에 따라 추정될 수 있습니다.
이 실험에서 힘의 벡터 특성을 검사하고 측정하였다. 벡터가 함께 추가되었고, 결과 크기 및 방향은 음량과 방향을 모두 실험적으로 결정하였다.
Tags
건너뛰기...
이 컬렉션의 비디오:

Now Playing
여러 방향의 벡터
Physics I
182.3K Views

뉴턴의 운동 법칙
Physics I
75.7K Views

힘과 가속
Physics I
79.1K Views

운동학 및 발사체 운동
Physics I
72.6K Views

뉴턴의 만유 인력 법칙
Physics I
190.9K Views

모멘텀 보존
Physics I
43.3K Views

마찰
Physics I
52.9K Views

후크의 법칙과 단순 조화 운동
Physics I
61.3K Views

평형 및 자유 물체 다이어그램
Physics I
37.3K Views

토크
Physics I
24.4K Views

회전 관성
Physics I
43.5K Views

각운동량
Physics I
36.2K Views

에너지와 일
Physics I
49.7K Views

엔탈피
Physics I
60.4K Views

엔트로피
Physics I
17.6K Views
Copyright © 2025 MyJoVE Corporation. 판권 소유