Vecteurs dans de multiples Directions

Source : Nicholas Timmons, Antonella Cooray, Ph.d., département de physique & astronomie, école de Sciences physique, University of California, Irvine, CA

Cette expérience montre comment les vecteurs addition et soustraction dans de multiples directions. L’objectif sera de calculer analytiquement l’addition ou la soustraction de vecteurs multiples puis confirmer expérimentalement les calculs.

Un vecteur est un objet avec grandeur et direction. L’ampleur d’un vecteur est simplement désigné comme la longueur, tandis que la direction est généralement définie par l’angle qu’il passe avec l’axe des x. Parce que les forces sont des vecteurs, il peuvent servir comme une représentation physique des vecteurs. Par la mise en place d’un système de forces et de trouver quel force supplémentaire permettra de créer un équilibre entre les forces, un système de vecteurs peut être vérifié expérimentalement.

Dans la Figure 1 montre le vecteur , ainsi que les axes x - et y -et l’angle θ que fait avec l’axe des x.

Figure 1 .

Pour ajouter ou soustraire deux vecteurs, il est utile de décrire le vecteur en fonction de ses composantes x - et y. La composante xest le montant du vecteur pointant dans la direction x -, qui est représentée mathématiquement comme :

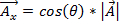. (Équation 1)

Le composant yest représenté par :

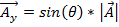. (Équation 2)

L’ampleur de la est défini comme étant :

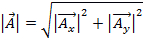. (Équation 3)

Pour ajouter ou soustraire deux vecteurs, simplement briser les vecteurs en leurs composants de x - et y -puis ajoutez ou soustrayez, respectivement, les composants correspondants.

Par exemple, si vecteur 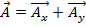et le vecteur 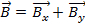, puis l’addition des deux vecteurs .

Pour déterminer l’angle θ un vecteur présente à l’égard de l’axe x, utilisez l’équation suivante :

. (Équation 4)

Vecteurs ayant grandeur et direction, multiplier deux vecteurs n’est pas aussi simple que la multiplication de deux nombres. Il existe deux façons de multiplier les vecteurs : le produit scalaire et le produit vectoriel. Le produit scalaire peut être écrite comme 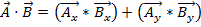ou 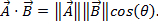ici, θ est l’angle entre deux vecteurs. Le résultat a seulement une magnitude et pas une direction. Une application du produit dot en physique est travail (W), où le travail est défini comme une force fois une distance 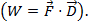le produit vectoriel de deux vecteurs peut être écrite comme 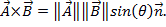alors que comme le produit scalaire, produit vectoriel contient le terme , qui est défini comme un vecteur avec magnitude 1 perpendiculaire à deux vecteurs et . Le résultat du produit vectoriel est un vecteur. Un exemple de produit vectoriel en physique est couple , qui est le résultat d’une force de fois un rayon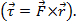

Les vecteurs sont utiles en physique comme la gravité ou la friction, les forces peuvent être représentées sous forme de vecteurs. Dans cet atelier, la force de gravité est utilisée pour démontrer la nature vectorielle des forces et comment ces forces ajouter dans de multiples directions. La force de gravité sur la surface de la terre s’écrit :

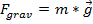, (Équation 5)

où est la masse de l’objet, tandis que est l’accélération de la pesanteur près de la surface terrestre (9,8 m/s²).

1. l’équilibre des forces.

1. Sur la table de force, mis en place deux poulies avec la même masse, face à des directions opposées (180° de différence dans l’angle).
2. La force de chacun sera égale à . Vérifiez si les deux forces sont égale et opposée, en examinant l’anneau au centre de la table de la force, qui ne doit pas bouger.
3. Notez que si les composantes des vecteurs associés à ces forces sont ajoutés, le vecteur qui en résulte aura zéro grandeur. C’est comment déterminer que toutes les forces sont en équilibre.

2. analyses calculs.

1. Cet atelier se composera de trois forces en équilibre. Deux forces seront appellera, tandis que le troisième sera le premier trouvé analytiquement, en utilisant la théorie des vecteurs et puis expérimentalement. Pour cet atelier, garder à 0° pour la durée.
2. Notez que si et sont connus et , lors de l’ajout au système, les deux forces pour être en équilibre, puis de causes est d’une ampleur égale, mais dans le sens inverse de la somme ( + ).
3. Calculer l’ampleur de la et . Utiliser le fait que et que 1 Newton (N) est une unité de force égale à .
4. En utilisant la théorie des vecteurs, calculer quelle ampleur serait si c’était la somme ( + ).
5. En utilisant la théorie des vecteurs, calculer quel angle serait si c’était la somme ( + ).

3. expérience.

1. Suivant les valeurs sur la première ligne du tableau 1 pour et , mis en place les deux forces sur la table de la force. N’oubliez pas de à 0°.
2. Mettre en place la troisième force, , en ajoutant des poids et en changeant l’angle jusqu'à ce que l’équilibre est atteint. Enregistrez ces valeurs dans le tableau 2.
3. Répétez l’étape 3.2 pour chacun des quatre cas.
4. Déterminer l’écart en pourcentage du résultat de l’analyse en calculant le 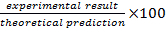. Remplir la Table 2 avec ces valeurs calculées.

Les résultats du laboratoire sont indiquées au tableau 1 et tableau 2.

Le tableau 1. Programme d’installation.

Installation #	A		B
	Messe	Angle	Messe	Angle
1	100	0	100	20
2	100	0	150	40
3	200	0	150	60
4	200	0	250	80

Le tableau 2. Résultats de l’analyse.

Installation #	Grandeur (N)	Grandeur (N)	Angle (°)	Grandeur (N)	Angle (°)
1	0,98	0,98	20	1.93	10
2	0,98	1.47	40	2.31	24
3	1,96	1.47	60	2,98	25
4	1,96	2.45	80	3.39	45

Tableau 3. Résultats expérimentaux.

Installation #	Grandeur expérimentale (N)	Magnitude analytique (N)	Différence (%)	Angle expérimental (°)	Angle de l’analyse (°)	Différence (%)
1	2.1	1.93	9	11	10	10
2	2.2	2.31	5	26	24	8
3	2.8	2,98	6	28	25	12
4	3.5	3.39	3	43	45	5

Les résultats de l’expérience sont en accord avec les calculs analytiques. La somme de deux vecteurs et l’angle entre eux peut être calculée à l’aide d’équations 1-5. Les équations sont valables pour effectuer des calculs de physiques vecteurs, tels que force.

Un voltigeur de baseball doit comprendre les vecteurs afin d’attraper une balle en mouvement. Si la position de voltigeur ne savait que la vitesse de la balle, il pourrait courir à leftfield plutôt qu’à droite et rater la balle. S’il ne savait que la direction de la frappe, il peut-être pratiquer, que de regarder le ballon naviguer au-dessus de sa tête. S’il comprend les vecteurs, puis dès que la balle est frappée, il peut considérer la grandeur et la direction afin d’estimer où la balle va être lorsqu’il effectue une capture.

Lorsqu’un avion est dans le ciel, sa vitesse et la direction peuvent être écrite comme un vecteur. Lorsqu’il y a un vent lourd, le vecteur vent ajoute au vecteur de l’avion pour donner le vecteur du système qui en résulte. Par exemple, si un avion vole dans le vent, l’amplitude du vecteur qui en résulte sera inférieur à la grandeur initiale. Cela correspond à l’avion se déplaçant plus lentement lorsque la position face au vent, ce qui donne un sens intuitif.

Lorsque deux objets entrent en collision et se serrer les coudes, le dynamisme de leur final (un vecteur) peut être approché comme la somme des deux vecteurs élan initial. Il s’agit d’une simplification, comme dans la vraie vie, deux objets en collision ont des facteurs supplémentaires à considérer, comme la chaleur ou la déformation de la collision. Momentum est juste la masse d’un objet multipliée par sa vitesse. Si deux patineurs sur glace voyageant dans des directions différentes et à des vitesses différentes s’entrechoquent et accrocher les uns aux autres, leur vitesse et direction finale peuvent être estimées d’après leurs composants du vecteur initial.

Dans cette expérience, la nature vectorielle des forces a été examinée et mesurée. Vecteurs ont été additionnées, et l’amplitude résultante et la direction ont été déterminées analytiquement et expérimentalement.