JoVE Science Education
Physics I
Hai accesso completo a questo contenuto tramite
Nanyang Technological UniversityVettori in più direzioni
Panoramica
Fonte: Nicholas Timmons, Asantha Cooray, PhD, Dipartimento di Fisica e Astronomia, Scuola di Scienze Fisiche, Università della California, Irvine, CA
Questo esperimento dimostra come i vettori aggiungono e sottraggono in più direzioni. L'obiettivo sarà quello di calcolare analiticamente l'addizione o la sottrazione di più vettori e quindi di confermare sperimentalmente i calcoli.
Un vettore è un oggetto con magnitudine e direzione. La grandezza di un vettore è semplicemente indicata come la lunghezza, mentre la direzione è tipicamente definita dall'angolo che fa con l'asse x. Poiché le forze sono vettori, possono essere utilizzate come rappresentazione fisica dei vettori. Impostando un sistema di forze e trovando quale forza aggiuntiva creerà un equilibrio tra le forze, un sistema di vettori può essere verificato sperimentalmente.
Principi
Nella Figura 1 mostra il vettore  , così come gli assi x e ye l'angolo θ che
, così come gli assi x e ye l'angolo θ che  fa con l'asse x-.
fa con l'asse x-.

Figura 1.
Per aggiungere o sottrarre due vettori, è utile descrivere il vettore in termini delle sue componenti x e y. La componente x-è la quantità del vettore che punta nella direzione x-,che è matematicamente rappresentata come:
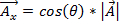 . (Equazione 1)
. (Equazione 1)
La componente yè rappresentata come:
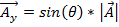 . (Equazione 2)
. (Equazione 2)
La grandezza di  è definita come:
è definita come:
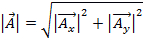 . (Equazione 3)
. (Equazione 3)
Per aggiungere o sottrarre due vettori, è sufficiente suddividere i vettori nelle loro componenti x e ye quindi aggiungere o sottrarre, rispettivamente, i componenti corrispondenti.
Ad esempio, se vettore 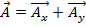 e vettore , quindi
e vettore , quindi 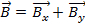 l'aggiunta dei due vettori
l'aggiunta dei due vettori  .
.
Per determinare l'angolo θ di un vettore rispetto all'asse x,utilizzare la seguente equazione:
 . (Equazione 4)
. (Equazione 4)
Poiché i vettori hanno sia magnitudine che direzione, moltiplicare due vettori non è semplice come moltiplicare due numeri. Esistono due modi per moltiplicare i vettori: il prodotto punto e il prodotto incrociato. Il prodotto punto può essere scritto come 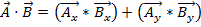 o
o 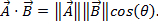 Qui, θ è l'angolo tra i due vettori. Il risultato ha solo una grandezza e non una direzione. Un'applicazione del prodotto punto in fisica è il lavoro (W), dove il lavoro è definito come una forza volte una distanza
Qui, θ è l'angolo tra i due vettori. Il risultato ha solo una grandezza e non una direzione. Un'applicazione del prodotto punto in fisica è il lavoro (W), dove il lavoro è definito come una forza volte una distanza 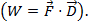 Il prodotto incrociato di due vettori può essere scritto come
Il prodotto incrociato di due vettori può essere scritto come 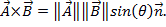 Mentre simile al prodotto punto, il prodotto incrociato contiene il termine
Mentre simile al prodotto punto, il prodotto incrociato contiene il termine  , che è definito come un vettore con magnitudine 1 che è perpendicolare ai due vettori
, che è definito come un vettore con magnitudine 1 che è perpendicolare ai due vettori  e
e  . Il risultato del prodotto incrociato è un vettore. Un esempio del prodotto incrociato in fisica è la coppia
. Il risultato del prodotto incrociato è un vettore. Un esempio del prodotto incrociato in fisica è la coppia  , che è il risultato di una forza volte un raggio
, che è il risultato di una forza volte un raggio 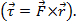
I vettori sono utili in fisica perché forze come la gravità o l'attrito possono essere rappresentate come vettori. In questo laboratorio, la forza di gravità viene utilizzata per dimostrare la natura vettoriale delle forze e come tali forze si sommano in più direzioni. La forza di gravità sulla superficie terrestre è scritta come:
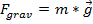 , (Equazione 5)
, (Equazione 5)
dove  è la massa dell'oggetto, mentre è
è la massa dell'oggetto, mentre è  l'accelerazione di gravità vicino alla superficie terrestre (9,8 m/s2).
l'accelerazione di gravità vicino alla superficie terrestre (9,8 m/s2).
Procedura
1. Bilanciere le forze.
- Sulla tabella di forza, impostare due pulegge con la stessa massa rivolta in direzioni opposte (differenza di angolo di 180 °).
- La forza di ciascuno sarà uguale a
 . Verificare se le due forze sono uguali e opposte esaminando l'anello al centro della tabella delle forze, che non dovrebbe muoversi.
. Verificare se le due forze sono uguali e opposte esaminando l'anello al centro della tabella delle forze, che non dovrebbe muoversi. - Si noti che se vengono aggiunti i componenti dei vettori associati a queste forze, il vettore risultante avrà magnitudine zero. Questo è il modo per determinare che tutte le forze sono in equilibrio.
2. Calcoli analitici.
- Questo laboratorio sarà composto da tre forze in equilibrio. Due forze saranno conosciute, mentre la terza sarà trovata- prima analiticamente, usando la teoria dei vettori, e poi sperimentalmente. Per questo laboratorio, mantenere
 a 0° per tutta la durata.
a 0° per tutta la durata. - Si noti che se
 e
e  sono noti e , quando aggiunti al sistema, fa sì che le due forze siano in
sono noti e , quando aggiunti al sistema, fa sì che le due forze siano in  equilibrio, allora è di
equilibrio, allora è di  uguale grandezza ma nella direzione opposta alla somma (
uguale grandezza ma nella direzione opposta alla somma (  +
+  ).
). - Calcola la grandezza di
 e
e  . Usa il fatto che
. Usa il fatto che  e che 1 Newton (N) è un'unità di forza uguale a
e che 1 Newton (N) è un'unità di forza uguale a  .
. - Usando la teoria dei vettori, calcola quale grandezza
 sarebbe se fosse la somma ( +
sarebbe se fosse la somma ( + 
 ).
). - Usando la teoria dei vettori, calcola quale angolo
 sarebbe se fosse la somma ( +
sarebbe se fosse la somma ( + 
 ).
).
3. Esperimento.
- Seguendo i valori sulla prima riga della tabella 1 per
 e ,
e ,  impostare le due forze sulla tabella delle forze. Ricordarsi di mantenersi
impostare le due forze sulla tabella delle forze. Ricordarsi di mantenersi  a 0°.
a 0°. - Impostare la terza forza,
 , aggiungendo pesi e cambiando l'angolo fino al raggiungimento dell'equilibrio. Registrare questi valori nella Tabella 2.
, aggiungendo pesi e cambiando l'angolo fino al raggiungimento dell'equilibrio. Registrare questi valori nella Tabella 2. - Ripetere il passaggio 3.2 per ciascuno dei quattro casi.
- Determinare la differenza percentuale dal risultato analitico calcolando
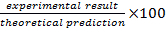 . Completare la Tabella 2 con questi valori calcolati.
. Completare la Tabella 2 con questi valori calcolati.
Risultati
I risultati del laboratorio sono mostrati nella Tabella 1 e nella Tabella 2.
Tabella 1. Apparecchio.
| Apparecchio # | Un | B | ||
| Un sacco | Angolo | Un sacco | Angolo | |
| 1 | 100 | 0 | 100 | 20 |
| 2 | 100 | 0 | 150 | 40 |
| 3 | 200 | 0 | 150 | 60 |
| 4 | 200 | 0 | 250 | 80 |
Tabella 2. Risultati analitici.
| Apparecchio # | Grandezza  (N) |
Grandezza  (N) |
Angolo  (°) |
Grandezza  (N) |
Angolo  (°) |
| 1 | 0.98 | 0.98 | 20 | 1.93 | 10 |
| 2 | 0.98 | 1.47 | 40 | 2.31 | 24 |
| 3 | 1.96 | 1.47 | 60 | 2.98 | 25 |
| 4 | 1.96 | 2.45 | 80 | 3.39 | 45 |
Tabella 3. Risultati sperimentali.
| Apparecchio # | Magnitudo sperimentale  (N) |
Grandezza analitica  (N) |
Differenza (%) |
Angolo sperimentale  (°) |
Angolo analitico (°) |
Differenza (%) |
| 1 | 2.1 | 1.93 | 9 | 11 | 10 | 10 |
| 2 | 2.2 | 2.31 | 5 | 26 | 24 | 8 |
| 3 | 2.8 | 2.98 | 6 | 28 | 25 | 12 |
| 4 | 3.5 | 3.39 | 3 | 43 | 45 | 5 |
I risultati dell'esperimento sono in accordo con i calcoli analitici. La somma di due vettori e l'angolo tra loro possono essere calcolati usando le equazioni 1-5. Le equazioni sono valide per fare calcoli di vettori fisici, come la forza.
Applicazione e Riepilogo
Un outfielder nel baseball deve capire i vettori per prendere una palla in movimento. Se l'esterno conoscesse solo la velocità della palla, potrebbe correre a sinistra invece che a destra e perdere la palla. Se solo conoscesse la direzione del colpo, potrebbe caricare, solo per guardare la palla navigare sopra la sua testa. Se capisce i vettori, non appena la palla viene colpita, può considerare sia la grandezza che la direzione per stimare dove sarà la palla quando fa una cattura.
Quando un aereo è nel cielo, la sua velocità e direzione possono essere scritte come un vettore. Quando c'è un vento forte, il vettore del vento si aggiunge al vettore del piano per dare il vettore del sistema risultante. Ad esempio, se un aereo sta volando nel vento, la magnitudine del vettore risultante sarà inferiore alla magnitudine iniziale. Questo corrisponde al piano che si muove più lentamente quando si dirige verso il vento, il che ha un senso intuitivo.
Quando due oggetti si scontrano e si attaccano insieme, il loro momento finale (un vettore) può essere approssimato come la somma dei due vettori di quantità di moto iniziali. Questa è una semplificazione, poiché nel mondo reale, due oggetti che si scontrano hanno fattori extra da considerare, come il calore o la deformazione dalla collisione. La quantità di moto è solo la massa di un oggetto moltiplicata per la sua velocità. Se due pattinatori sul ghiaccio che viaggiano in direzioni diverse e a velocità diverse si scontrano e si aggrappano l'uno all'altro, la loro direzione e velocità finali possono essere stimate in base alle loro componenti vettoriali iniziali.
In questo esperimento, la natura vettoriale delle forze è stata esaminata e misurata. I vettori sono stati sommati e la magnitudine e la direzione risultanti sono state determinate sia analiticamente che sperimentalmente.
Vai a...
Video da questa raccolta:

Now Playing
Vettori in più direzioni
Physics I
182.4K Visualizzazioni

I principi della dinamica (leggi di Newton)
Physics I
76.0K Visualizzazioni

Forza e accelerazione
Physics I
79.2K Visualizzazioni

Cinematica e moto parabolico
Physics I
72.7K Visualizzazioni

Legge di gravitazione universale di Newton
Physics I
191.6K Visualizzazioni

Conservazione del momento angolare
Physics I
43.4K Visualizzazioni

Attrito
Physics I
52.9K Visualizzazioni

Legge di Hooke e moto armonico semplice
Physics I
61.4K Visualizzazioni

Diagrammi di equilibrio e corpo libero
Physics I
37.4K Visualizzazioni

Momento meccanico
Physics I
25.0K Visualizzazioni

Momento di inerzia
Physics I
43.6K Visualizzazioni

Momento angolare
Physics I
36.3K Visualizzazioni

Energia e lavoro
Physics I
50.0K Visualizzazioni

Entalpia
Physics I
60.4K Visualizzazioni

Entropia
Physics I
17.7K Visualizzazioni
Copyright © 2025 MyJoVE Corporation. Tutti i diritti riservati
Utilizziamo i cookies per migliorare la tua esperienza sul nostro sito web.
Continuando a utilizzare il nostro sito web o cliccando “Continua”, accetti l'utilizzo dei cookies.