Vetores em Múltiplas Direções

Fonte: Nicholas Timmons, Asantha Cooray, PhD, Departamento de Física & Astronomia, Escola de Ciências Físicas, Universidade da Califórnia, Irvine, CA

Este experimento demonstra como os vetores adicionam e subtraem em várias direções. O objetivo será calcular analiticamente a adição ou subtração de múltiplos vetores e, em seguida, confirmar experimentalmente os cálculos.

Um vetor é um objeto com magnitude e direção. A magnitude de um vetor é simplesmente denotada como o comprimento, enquanto a direção é tipicamente definida pelo ângulo que faz com o eixo x. Como as forças são vetores, elas podem ser usadas como uma representação física dos vetores. Ao criar um sistema de forças e descobrir qual força adicional criará um equilíbrio entre as forças, um sistema de vetores pode ser verificado experimentalmente.

Na Figura 1 mostra o vetor, bem como os eixos x e ye o ângulo que faz com o eixo x.

Figura 1.

Para adicionar ou subtrair dois vetores, é útil descrever o vetor em termos de seus componentes x e y. O componente xé a quantidade do vetor que aponta na direção x,que é matematicamente representada como:

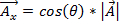. (Equação 1)

O componente yé representado como:

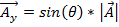. (Equação 2)

A magnitude de é definida como:

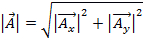. (Equação 3)

Para adicionar ou subtrair dois vetores, basta quebrar os vetores em seus componentes x e y e,em seguida, adicionar ou subtrair, respectivamente, os componentes correspondentes.

Por exemplo, se vetor 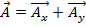e 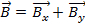vetor, então a adição dos dois vetores .

Para determinar o ângulo que um vetor faz em relação ao eixo x,use a seguinte equação:

. (Equação 4)

Como os vetores têm magnitude e direção, multiplicar dois vetores não é tão simples quanto multiplicar dois números. Existem duas maneiras de multiplicar vetores: o produto ponto e o produto cruzado. O produto ponto pode ser escrito como 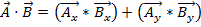ou 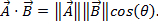aqui, φ é o ângulo entre os dois vetores. O resultado só tem uma magnitude, e não uma direção. Uma aplicação do produto ponto na física é o trabalho (W), onde o trabalho é definido como uma força vezes à distância 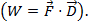O produto cruzado de dois vetores pode ser escrito como 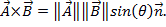Enquanto semelhante ao produto ponto, o produto cruzado contém o termo , que é definido como um vetor com magnitude 1 que é perpendicular aos dois vetores e . O resultado do produto cruzado é um vetor. Um exemplo do produto cruzado na física é o torque, que é o resultado de uma força vezes por raio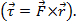

Vetores são úteis na física porque forças como gravidade ou atrito podem ser representadas como vetores. Neste laboratório, a força da gravidade é usada para demonstrar a natureza vetorial das forças e como essas forças adicionam em múltiplas direções. A força da gravidade na superfície da Terra está escrita como:

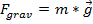, (Equação 5)

onde está a massa do objeto, enquanto é a aceleração da gravidade perto da superfície da Terra (9,8 m/s²).

1. Forças de equilíbrio.

1. Na mesa de força, configure duas polias com a mesma massa voltada para direções opostas (180° diferença no ângulo).
2. A força de cada um será igual a . Verifique se as duas forças são iguais e opostas examinando o anel no centro da tabela de força, que não deve se mover.
3. Observe que se os componentes dos vetores associados a essas forças forem adicionados, o vetor resultante terá magnitude zero. É assim que se determina que todas as forças estão em equilíbrio.

2. Cálculos analíticos.

1. Este laboratório consistirá de três forças em equilíbrio. Duas forças serão conhecidas, enquanto a terceira será encontrada em primeiro lugar analiticamente, usando a teoria dos vetores, e depois experimentalmente. Para este laboratório, mantenha-se em 0° durante a duração.
2. Note que se e são conhecidos e, quando adicionados ao sistema, faz com que as duas forças estejam em equilíbrio, então é de igual magnitude, mas na direção oposta à soma ( + ).
3. Calcule a magnitude de e. Use o fato de que e que 1 Newton (N) é uma unidade de força igual a .
4. Usando a teoria dos vetores, calcule qual seria a magnitude se fosse a soma ( + ).
5. Usando a teoria dos vetores, calcule qual seria o ângulo se fosse a soma ( + ).

3. Experimente.

1. Seguindo os valores na primeira linha da Tabela 1 para e , configurar as duas forças na tabela de força. Lembre-se de manter a 0°.
2. Configure a terceira força, adicionando pesos e mudando o ângulo até que o equilíbrio seja alcançado. Registo esses valores na Tabela 2.
3. Repita a etapa 3.2 para cada um dos quatro casos.
4. Determine a diferença percentual do resultado analítico calculando o 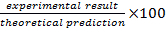. Tabela Completa 2 com estes valores calculados.

Os resultados do laboratório são mostrados na Tabela 1 e Tabela 2.

Mesa 1. Configuração.

Configuração #	Um		B
	Missa	Ângulo	Missa	Ângulo
1	100	0	100	20
2	100	0	150	40
3	200	0	150	60
4	200	0	250	80

Mesa 2. Resultados Analíticos.

Configuração #	Magnitude (N)	Magnitude (N)	Ângulo (°)	Magnitude (N)	Ângulo (°)
1	0.98	0.98	20	1.93	10
2	0.98	1.47	40	2.31	24
3	1.96	1.47	60	2.98	25
4	1.96	2.45	80	3.39	45

Mesa 3. Resultados experimentais.

Configuração #	Experimental Magnitude (N)	Magnitude Analítica (N)	Diferença (%)	Ângulo Experimental (°)	Ângulo Analítico (°)	Diferença (%)
1	2.1	1.93	9	11	10	10
2	2.2	2.31	5	26	24	8
3	2.8	2.98	6	28	25	12
4	3.5	3.39	3	43	45	5

Os resultados do experimento estão de acordo com os cálculos analíticos. A soma de dois vetores e o ângulo entre eles podem ser calculados usando equações 1-5. As equações são válidas para fazer cálculos de vetores físicos, como a força.

Um jogador de beisebol tem que entender vetores para pegar uma bola em movimento. Se o defensor soubesse apenas a velocidade da bola, ele poderia correr para o campo esquerdo em vez de para a direita e errar a bola. Se ele soubesse a direção do golpe, ele poderia atacar, apenas para ver a bola passar por cima de sua cabeça. Se ele entende vetores, então assim que a bola é atingida, ele pode considerar tanto a magnitude e a direção, a fim de estimar onde a bola vai estar quando ele faz uma captura.

Quando um avião está no céu, sua velocidade e direção podem ser escritas como um vetor. Quando há um vento forte, o vetor de vento adiciona ao vetor do avião para dar o vetor do sistema resultante. Por exemplo, se um avião está voando contra o vento, a magnitude do vetor resultante será menor do que a magnitude inicial. Isso corresponde ao avião se movendo mais devagar quando se dirige para o vento, o que faz sentido intuitivo.

Quando dois objetos colidem e ficam juntos, seu momento final (um vetor) pode ser aproximado como a soma dos dois vetores de momento inicial. Trata-se de uma simplificação, pois no mundo real, dois objetos colidindo têm fatores extras a considerar, como calor ou deformação da colisão. O momento é apenas a massa de um objeto multiplicado por sua velocidade. Se dois patinadores no gelo viajando em direções diferentes e em velocidades diferentes colidem e se agarram um ao outro, sua direção final e velocidade podem ser estimadas com base em seus componentes vetoriais iniciais.

Neste experimento, a natureza vetorial das forças foi examinada e medida. Os vetores foram somados, e a magnitude e direção resultantes foram determinadas tanto analiticamente quanto experimentalmente.