Vectors in Multiple Directions

Source: Nicholas Timmons, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA

This experiment demonstrates how vectors add and subtract in multiple directions. The goal will be to analytically calculate the addition or subtraction of multiple vectors and then to experimentally confirm the calculations.

A vector is an object with both magnitude and direction. The magnitude of a vector is simply denoted as the length, while the direction is typically defined by the angle it makes with the x-axis. Because forces are vectors, they can be used as a physical representation of vectors. By setting up a system of forces and finding which additional force will create an equilibrium between the forces, a system of vectors can be experimentally verified.

In Figure 1 shows the vector , as well as the x- and y-axes and the angle θ that makes with the x-axis.

Figure 1.

To add or subtract two vectors, it is useful to describe the vector in terms of its x- and y-components. The x-component is the amount of the vector that points in the x-direction, which is mathematically represented as:

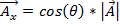. (Equation 1)

The y-component is represented as:

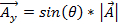. (Equation 2)

The magnitude of  is defined to be:

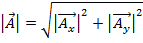. (Equation 3)

To add or subtract two vectors, simply break the vectors down into their x- and y-components and then add or subtract, respectively, the corresponding components.

For example, if vector 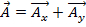and vector 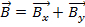, then the addition of the two vectors .

To determine the angle θ a vector makes with respect to the x-axis, use the following equation:

. (Equation 4)

Because vectors have both magnitude and direction, multiplying two vectors is not as simple as multiplying two numbers. There are two ways to multiply vectors: the dot product and the cross product. The dot product can be written as 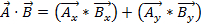 or 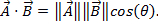  Here, θ is the angle between the two vectors. The result only has a magnitude, and not a direction. An application of the dot product in physics is work (W), where work is defined as a force times a distance 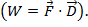The cross product of two vectors can be written as 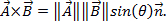While similar to the dot product, the cross product contains the term , which is defined as a vector with magnitude 1 that is perpendicular to the two vectors and 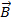. The result of the cross product is a vector. One example of the cross product in physics is torque , which is the result of a force times a radius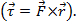

Vectors are useful in physics because forces like gravity or friction can be represented as vectors. In this lab, the force of gravity is used to demonstrate the vector nature of forces and how those forces add in multiple directions. The force of gravity on the Earth's surface is written as:

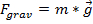, (Equation 5)

where is the mass of the object, while  is the acceleration of gravity near the Earth's surface (9.8 m/s²).

1. Balance forces.

1. On the force table, set up two pulleys with the same mass facing opposite directions (180° difference in angle).
2. The force of each will be equal to . Check whether the two forces are equal and opposite by examining the ring at the center of the force table, which should not move.
3. Notice that if the components of the vectors associated with these forces are added, the resultant vector will have zero magnitude. This is how to determine that all forces are in equilibrium.

2. Analytical calculations.

1. This lab will consist of three forces in equilibrium. Two forces will be known, while the third will be found-first analytically, using the theory of vectors, and then experimentally. For this lab, keep at 0° for the duration.
2. Note that if and 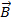 are known and , when added to the system, causes the two forces to be in equilibrium, then is of equal magnitude but in the opposite direction to the sum (  +  ).
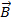3. Calculate the magnitude of and 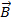. Use the fact that and that 1 Newton (N) is a unit of force equal to .
4. Using the theory of vectors, calculate what magnitude  would be if it was the sum (  +  ).
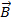5. Using the theory of vectors, calculate what angle would be if it was the sum (  +  ).

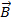3. Experiment.

1. Following the values on the first line of Table 1 for  and 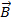, set up the two forces on the force table. Remember to keep  at 0°.
2. Set up the third force, , by adding weights and changing the angle until equilibrium is reached. Record these values in Table 2.
3. Repeat step 3.2 for each of the four cases.
4. Determine the percent difference from the analytical result by calculating the 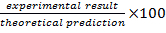. Complete Table 2 with these calculated values.

The results of the lab are shown in Table 1 and Table 2.

Table 1. Setup.

Setup #	A		B
	Mass	Angle	Mass	Angle
1	100	0	100	20
2	100	0	150	40
3	200	0	150	60
4	200	0	250	80

Table 2. Analytical Results.

Setup #	Magnitude (N)	Magnitude 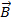(N)	Angle 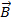(°)	Magnitude (N)	Angle (°)
1	0.98	0.98	20	1.93	10
2	0.98	1.47	40	2.31	24
3	1.96	1.47	60	2.98	25
4	1.96	2.45	80	3.39	45

Table 3. Experimental Results.

Setup #	Experimental Magnitude (N)	Analytical Magnitude (N)	Difference (%)	Experimental Angle (°)	Analytical Angle (°)	Difference (%)
1	2.1	1.93	9	11	10	10
2	2.2	2.31	5	26	24	8
3	2.8	2.98	6	28	25	12
4	3.5	3.39	3	43	45	5

The results of the experiment are in agreement with the analytical calculations. The sum of two vectors and the angle between them can be calculated using Equations 1-5. The equations are valid for making calculations of physical vectors, such as force.

An outfielder in baseball has to understand vectors in order to catch a ball on the move. If the outfielder only knew the speed of the ball, he might run to leftfield instead of to right and miss the ball. If he only knew the direction of the hit, he might charge in, only to watch the ball sail over his head. If he understands vectors, then as soon as the ball is hit, he can consider both the magnitude and direction in order to estimate where the ball is going to be when he makes a catch.

When an airplane is in the sky, its speed and direction can be written as a vector. When there is a heavy wind, the wind vector adds to the vector of the plane to give the resultant system vector. For example, if a plane is flying into the wind, the magnitude of the resultant vector will be less than the initial magnitude. This corresponds to the plane moving slower when heading into the wind, which makes intuitive sense.

When two objects collide and stick together, their final momentum (a vector) can be approximated as the sum of the two initial momentum vectors. This is a simplification, as in the real world, two objects colliding have extra factors to consider, like heat or deformation from the collision. Momentum is just the mass of an object multiplied by its velocity. If two skaters on ice traveling in different directions and at different speeds collide and hold onto each other, their final direction and speed can be estimated based upon their initial vector components.

In this experiment, the vector nature of forces was examined and measured. Vectors were added together, and the resultant magnitude and direction were determined both analytically and experimentally.