Conservazione dell'energia come approccio all'analisi del sistema

Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Dipartimento di Ingegneria Meccanica, Michigan State University, East Lansing, MI

Lo scopo di questo esperimento è dimostrare l'applicazione dell'equazione di risparmio energetico per determinare le prestazioni di un sistema di flusso. A tal fine, l'equazione energetica per un flusso costante e incomprimibile viene applicata a un tubo corto con una valvola a saracinesca. La valvola a saracinesca viene quindi gradualmente chiusa e viene caratterizzata la sua influenza sulle condizioni di flusso. Inoltre, l'interazione tra questo sistema di flusso e la ventola che aziona il flusso viene studiata confrontando la curva del sistema con la curva caratteristica della ventola.

Questo esperimento aiuta a capire come la dissipazione di energia viene utilizzata dalle valvole per limitare il flusso. Inoltre, secondo lo stesso principio, questo esperimento offre un metodo semplice per misurare la portata utilizzando la variazione di pressione attraverso un ingresso brusco.

L'analisi del flusso del fluido viene spesso eseguita in base a come l'energia si trasforma mentre il fluido scorre attraverso un sistema. L'energia totale trasportata da un flusso include energia cinetica, potenziale e termodinamica. Queste forme di energia possono trasformarsi l'una nell'altra liberamente, e l'energia contenuta nel flusso in una data posizione in un sistema di flusso è l'equilibrio tra l'energia totale in entrata, l'energia aggiunta e l'energia sottratta. Questo bilancio energetico può essere espresso in forma di equazione come segue [1, 2]:

(1)

Qui, i sottoindici 1 e 5 si riferiscono rispettivamente alle condizioni di ingresso e di uscita del sistema di flusso. La Figura 2(A) mostra uno schema del sistema di flusso: l'aria entra attraverso un sistema di condizionamento del flusso, o contrazione, chiamato plenum (il suo scarico mostrato nella Figura 3(A)). Quindi, passa a un tubo corto con una valvola alla sua estremità (vedere la Figura 2 (B) per i dettagli del sistema tubo/ valvola e le Figure 2 (A) e (B) per le immagini). L'aria scarica dalla valvola in uno spazio chiuso isolato dall'esterno chiamato "ricevitore" (vedere la Figura 3 per riferimento). Come mostrato nella Figura 3, il ricevitore è abbastanza grande da ospitare il sistema di acquisizione dati e gli sperimentatori. Infine, il flusso esce dal ricevitore attraverso una piastra perforata che funge da ammortizzatore per la regolazione del flusso (vedere la Figura 3 (C) per riferimento). L'aria viene quindi catturata da un ventilatore centrifugo che scarica di nuovo nell'atmosfera. I termini tra parentesi rappresentano il contenuto energetico specifico in ogni porta, che è la somma di energia potenziale gravitazionale , energia cinetica 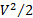e energia termodinamica (o potenziale di pressione). Il coefficiente viene utilizzato per tenere conto della forma del profilo di velocità. Per il presente esperimento 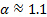perché il flusso è turbolento [1, 2]. Come tale, il lato sinistro dell'equazione (1) rappresenta la variazione del contenuto energetico tra le porte di entrata e di uscita. In assenza di lavoro esterno o effetti dissipativi, questa differenza è zero. Tuttavia, la maggior parte delle applicazioni ingegneristiche che coinvolgono flussi reali includono l'addizione o la sottrazione di energia per mezzo di macchinari di flusso e gli effetti dissipativi, . Questi due effetti sono inclusi sul lato destro dell'equazione (1).

In questo esperimento, verrà utilizzato un ventilatore centrifugo per indurre il flusso, cioè per aggiungere energia al fluido. Per questo tipo di macchina, il termine è una funzione della portata chiamata curva caratteristica ed è determinato sperimentalmente:

(2)

Qui, 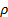e sono la densità e la viscosità cinematica dell'aria in condizioni locali, ed 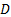è il diametro del sistema di flusso (mm nel presente esperimento). L'equazione (2) è in una forma che assicura che le costanti nel primo e nel secondo termine siano adimensionali, mentre la costante nel terzo termine è in unità di pressione (Pa) per garantire l'omogeneità dimensionale. L'equazione (2) è la "curva delle prestazioni della ventola" mostrata nella Figura 1.

Infine, la dissipazione di energia è proporzionale all'energia cinetica del flusso:

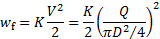(3)

Si noti che, usando l'equazione di continuità ( , dove 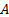è l'area della sezione trasversale [1, 2]), la dissipazione di energia può anche essere scritta in termini di portata, . La Figura 1 presenta quest'ultima forma di equazione (3) come "Curva del sistema di flusso". Nell'equazione (3), il coefficiente di proporzionalità , è chiamato coefficiente di perdita ed è l'aggiunta di tutti gli effetti dissipativi indotti dagli elementi del sistema di flusso come risultato di interazioni viscose. Mentre i contributi di tubi e condotti dipendono dalla loro rugosità, lunghezza e numero di Reynolds, il contributo di raccordi per tubi, ingressi e scarichi, espansioni, contrazioni, curve e valvole dipende dalle loro particolari geometrie. Per il presente esperimento, il coefficiente di perdita complessivo è la combinazione di un ingresso, una valvola e una scarica:

(4)

Dove sono e rispettivamente i valori dei coefficienti di perdita per l'ingresso e lo 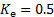scarico (cfr. [1, 2] per riferimento). Il coefficiente di perdita per la valvola, 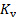, sarà discusso nella sezione seguente.

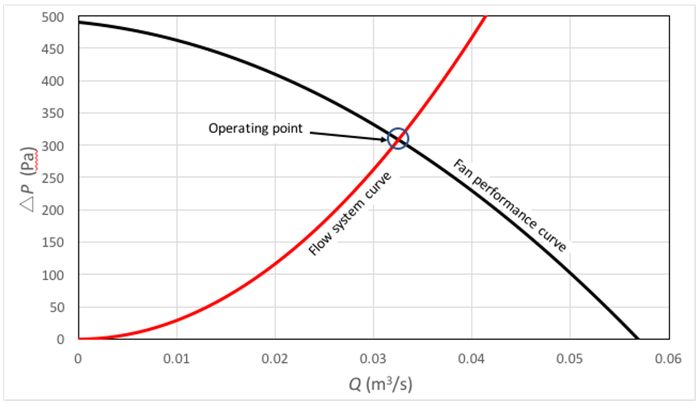
Figura 1. Esempio di curva di sistema e curva delle prestazioni della ventola. : curva di sistema; : curva delle prestazioni della ventola. Il cerchio blu evidenzia l'intersezione tra entrambe le curve, che è il punto operativo.

Figura 2. Impostazione sperimentale. (A): Impianto di flusso. Il flusso si sposta da sinistra a destra; entra nel plenum attraverso una sezione di condizionamento del flusso, quindi scorre attraverso il tubo e la valvola, scarica all'interno del ricevitore e infine esce dal sistema attraverso la ventola. (B): dettagli del sistema di flusso e delle apparecchiature di acquisizione dati. Fare clic qui per visualizzare una versione più grande di questa figura.

Figura 3. Sistema di acquisizione dati. (A) Le connessioni di questi dispositivi di acquisizione dati seguono il diagramma nella Figura 2(B). (B) Interfaccia virtuale per l'acquisizione dati (scritta in LabView). Fare clic qui per visualizzare una versione più grande di questa figura.

Caratteristiche di dissipazione di una valvola

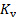Poiché le valvole sono essenzialmente dispositivi a geometria variabile, il loro coefficiente di perdita specifico è una funzione dell'angolo di rotazione del loro albero ( ). Con questo in mente, varia come la valvola viene aperta o chiusa in base alla seguente relazione:

(5)

Qui, abbiamo usato di nuovo l'equazione di continuità per esprimere il coefficiente di perdita in termini di portata. Inoltre, l'equazione (5) suggerisce che possiamo determinare il coefficiente di perdita per la valvola conoscendo il valore della portata e della caduta di pressione attraverso la valvola in funzione dell'angolo di apertura e della portata: . Questa è anche la differenza di pressione tra i punti 3 e 4 della figura 2(B) ( ).

Punto di funzionamento

Come mostrato in Figura 1, il punto operativo di un sistema di flusso azionato da una macchina a flusso, come quello descritto in questo esperimento, è dato dal punto di intersezione della curva caratteristica del ventilatore e della curva del sistema di flusso. Questo punto può essere caratterizzato utilizzando l'equazione dell'energia come segue: come si può vedere nella Figura 2 (A), l'aria entra nel sistema di flusso da una grande stanza in condizioni atmosferiche ed esce nella stessa stanza senza alcun cambiamento significativo di altezza. Di conseguenza, le condizioni di pressione, velocità e altezza all'ingresso e all'uscita del sistema 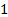(e i sottoindici nell'equazione (1) rispettivamente) sono identiche e si annullano a vicenda. Di conseguenza, l'energia aggiunta dalla ventola è bilanciata dall'energia dissipata dal sistema di flusso. In altre parole, le equazioni (2) e (3) formano un'uguaglianza che si traduce nella seguente relazione dopo la semplificazione:

(6)

La radice positiva di questa equazione esprime il Punto Operativo:

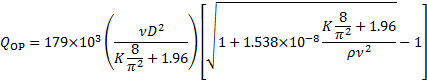(7)

Qui, il sottointedice "OP" sta per "Punto operativo". Il coefficiente di perdita nell'equazione (7) è l'aggiunta dei coefficienti di perdita dell'ingresso, della valvola e dello scarico. Dalle equazioni (4) e (5):

(8)

Misurazione della portata

Analogamente a tutte le analisi precedenti, l'equazione (1) viene applicata tra il plenum e un punto a valle dell'ingresso acuto (punti 2 e 3 nella figura 2 (B)) per recuperare la seguente equazione:

(9)

Qui, abbiamo usato il fatto che non c'è alcun cambiamento di altezza tra i punti 2 e 3, e la velocità all'interno del plenum è trascurabile. Introducendo l'equazione di continuità ( 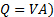e l'equazione (3), arriviamo alla seguente relazione per la portata in termini di differenza di pressione tra il plenum (punto 2 nella figura 2 (B)) e la pressione statica a monte della valvola (punto 3 nella figura 2 (B)):

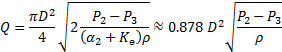(10)

La costante 0,878 si ottiene dopo aver sostituito i valori del coefficiente di perdita e della correzione della velocità 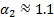(e 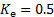, vedi [1, 2] per riferimento) e raggruppando tutte le costanti in una sola.

1. Impostazione della struttura

1. Assicurati che la ventola non sia in funzione, quindi non ci sia flusso nella struttura.
2. Verificare che il sistema di acquisizione dati (Figura 4(A)) segua lo schema di cui alla figura 2B.
   1. Collegare la porta positiva del trasduttore di pressione #1 (vedere figura 2B per riferimento) al rubinetto di pressione a monte della valvola ( ).
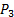   2. Lasciare la porta negativa del trasduttore di pressione #1 aperta alle condizioni della stanza (ricevitore: 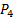). Quindi, la lettura di questo trasduttore sarà direttamente .
   3. Collegare la porta positiva del trasduttore di pressione #2 (vedere la figura 2B per riferimento) al rubinetto di pressione del plenum ( ).
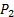   4. Collegare la porta negativa del trasduttore di pressione #2 (vedere figura 2B per riferimento) al rubinetto di pressione a monte della valvola ( 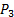). Quindi, la lettura di questo trasduttore sarà direttamente , come richiesto dall'equazione (10).
3. Assicurarsi che il canale virtuale 0 nel sistema di acquisizione dati (Figura 4(B)) corrisponda al trasduttore di pressione #1 ( ) e che il canale virtuale 1 corrisponda al trasduttore di pressione #2 ( ).
4. Impostare il sistema di acquisizione dati per campionare ad una velocità di 100 Hz per un totale di 500 campioni (cioè 5s di dati).

Tabella 1. Parametri di base per lo studio sperimentale.

Parametro	Valore
Diametro tubo (D)	50,8 mm (2 pollici)
Costante di calibrazione #1 del trasduttore (m_p1)	Pa/V
Costante di calibrazione #2 del trasduttore (m_p2)	Pa/V
Pressione atmosferica locale	100.474,15 Pa
Temperatura locale	297,15 K
Densità dell'aria locale	1,186 kg/m3

Figura 4. Impianto di flusso. (A): vista dello scarico del plenum nella sezione del ricevitore prima di installare il set di valvole da studiare. (B): tre diversi tipi di valvole all'interno del ricevitore. Da sinistra a destra: valvola a saracinesca, valvola a globo, valvola a farfalla. (C): porte di uscita dal ricevitore. Le valvole scaricano il flusso all'interno del ricevitore e la ventola aspira il flusso dal ricevitore attraverso la piastra perforata nella foto. Fare clic qui per visualizzare una versione più grande di questa figura.

2. Misurazioni

1. Registrare il diametro del tubo collegato alla valvola e calcolarne l'area della sezione trasversale.
2. Determinare il numero massimo di giri completi della maniglia necessari per spostare la valvola dalla posizione completamente chiusa alla posizione completamente aperta. Se questo numero non è un numero intero, escludere l'ultima rotazione frazionaria per semplificare l'analisi. Per l'esperimento corrente, il numero massimo di giri completi è 12.
3. Chiudere completamente la valvola.
4. Ruotare l'impugnatura della valvola fino a quando non è completamente aperta contando il numero di giri completi. Per semplicità, utilizzare solo un numero intero di giri per l'esperimento. Ad esempio, ci vogliono circa 12 giri e 1/3 di giro per aprire completamente la valvola utilizzata in questo esperimento. Quindi, gireremo la maniglia di questa valvola solo 12 giri completi dalla sua posizione completamente chiusa e la definiremo come la posizione iniziale ( ).
5. Accendere la struttura di flusso.
6. Utilizzare il sistema di acquisizione dati per registrare le letture di e .
7. Inserire nella tabella 2 i valori medi di e ottenuti con il sistema di acquisizione dati.
8. Chiudere la valvola di 1,5 giri.
9. Ripetere i passaggi da 2.6 a 2.8 fino a quando la tabella 2 non è completamente popolata.
10. Spegnere la struttura di flusso.

3. Analisi dei dati

1. Determinare il coefficiente di perdita della valvola per ogni posizione angolare utilizzando l'equazione (5). Immettere questi valori nella tabella 2.
2. Determinare la portata per ogni posizione angolare della valvola utilizzando l'equazione (10). Immettere questi valori nella tabella 2.
3. Determinare il punto operativo utilizzando l'equazione (7). Immettere questi valori nella tabella 2.
4. Calcolare la differenza relativa tra la portata misurata e il punto operativo
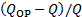
5. Utilizzate l'equazione (3) per produrre un grafico delle curve di sistema per tutti i valori di 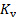. Si consideri il coefficiente di perdita totale come .
6. Aggiungete la curva caratteristica della ventola a questo stesso plottaggio utilizzando l'equazione (2).

Tabella 2. Risultati rappresentativi. Misurazioni delle differenze di pressione e stime dei coefficienti di portata e di perdita.

[P_pl-P_a ] (Pa)	[P_a-P_r ] (Pa)	Q (m3/s)	Okay	Q_OP (m3/s)	ε (%)
246.75	54.00	0.0327	0.450	0.0316	-3.16
208.62	114.22	0.0301	0.976	0.0293	-2.51
156.19	204.80	0.0260	2.198	0.0254	-2.30
109.30	281.69	0.0218	4.224	0.0214	-1.53
71.82	348.38	0.0176	7.863	0.0174	-1.26
38.72	408.60	0.0129	16.989	0.0128	-0.90
15.00	452.39	0.0081	48.359	0.0080	-0.32
2.51	482.50	0.0033	307.799	0.0033	-0.18

La Figura 5 mostra i risultati per le misurazioni correnti. Qui, la linea solida nera è stata generata con l'equazione (2) e ogni linea rossa con l'equazione (3) per diversi valori del coefficiente di perdita della valvola. Dalla figura, è evidente che la curva del sistema aumenta la sua pendenza man mano che la valvola si chiude. In altre parole, questo esperimento dimostra che il principio alla base del funzionamento di una valvola è quello di aumentare la dissipazione di energia per limitare il flusso. D'altra parte, dall'equazione (5), si potrebbe dedurre che il valore di 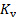diventa infinito quando la valvola è completamente chiusa. Concettualmente, questa condizione significa che tutta l'energia viene dissipata, quindi impedisce completamente il flusso attraverso la valvola.

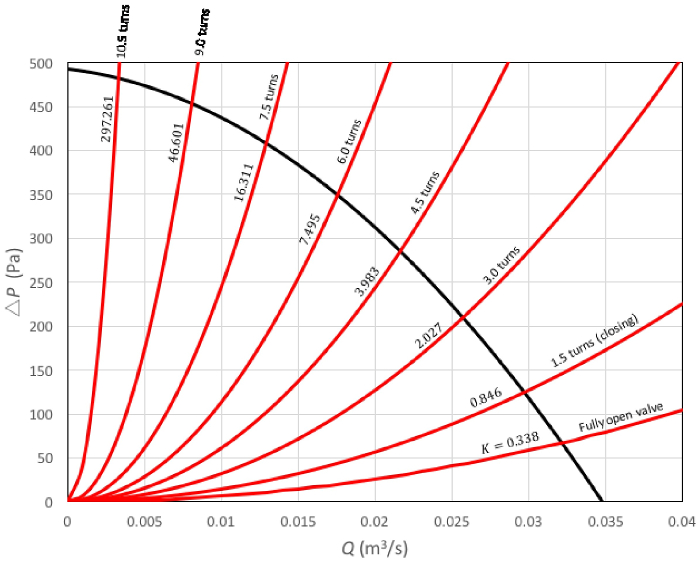
Figura 5. Risultati rappresentativi. : curve di sistema. Ogni curva di questa famiglia è il risultato di un diverso grado di apertura della valvola. La pendenza delle curve aumenta man mano che la valvola viene chiusa. Ogni curva ha il suo coefficiente di perdita corrispondente come riferimento; : curva delle prestazioni della ventola. Fare clic qui per visualizzare una versione più grande di questa figura.

Come mostrato nella tabella 2, l'errore tra la portata stimata nel punto operativo (equazione (7)) e la portata misurata (equazione (10)) rimane inferiore al 3,2% per l'intervallo di portata studiato. Sebbene questo sia un risultato soddisfacente dato il piccolo errore percentuale, la portata stimata nel punto operativo è sempre sottostimata e segue una tendenza decrescente man mano che la valvola viene gradualmente chiusa. Questa tendenza offre alcune informazioni sul comportamento del sistema di flusso, in particolare perché il valore del fattore di correzione per la non uniformità della velocità aumenta leggermente con il numero di Reynolds. Non sorprende quindi che l'errore aumenti con la portata.

Questo esperimento ha esplorato l'applicazione dell'equazione energetica per caratterizzare l'azione di una valvola sul flusso del tubo. È stato osservato che la valvola induce resistenza al flusso aumentando la dissipazione di energia. Considerando che la caduta di pressione lungo il sistema di flusso è direttamente proporzionale al quadrato della portata, l'effetto della dissipazione di energia è catturato dall'entità del coefficiente di proporzionalità. Questo coefficiente è l'aggiunta dei coefficienti di perdita di tutti gli elementi del sistema di flusso, compresa la valvola. Il coefficiente di perdita della valvola aumenta monotonamente man mano che la valvola viene gradualmente chiusa. E questo effetto aumenta di conseguenza la pendenza della curva del sistema, raggiungendo un valore di infinito quando la valvola è completamente chiusa.

Il comportamento sopra descritto è stato contrastato con la curva delle prestazioni del ventilatore centrifugo che guida il flusso. Confrontando la portata misurata direttamente con la portata stimata dall'intersezione della curva di sistema e la curva di prestazione del ventilatore, è stato dimostrato che questo punto di intersezione definisce le condizioni operative della portata e della domanda di pressione.

Questo esperimento ha seguito allo scopo di dimostrare i principi del risparmio energetico per caratterizzare alcune diverse applicazioni ingegneristiche: funzionamento della valvola, misurazione della portata e condizioni operative di un sistema di flusso. Il risparmio energetico può essere utilizzato fondamentalmente per caratterizzare qualsiasi sistema di flusso, questi sono altri due esempi di applicazioni dell'equazione energetica:

L'energia cinetica trasportata dal vento può essere raccolta dalle turbine eoliche per produrre energia elettrica. Confrontando a monte con le condizioni di flusso a valle, l'equazione dell'energia può essere utilizzata per valutare quanta energia è stata rimossa dal vento. L'entità dell'energia recuperata sarà data dal lavoro dell'albero, , nell'equazione (1).

Il cambiamento nell'energia potenziale gravitazionale può essere utilizzato per valutare la portata d'acqua su uno sfioratore. Questo viene fatto in combinazione con l'equazione di conservazione della massa misurando le profondità a monte e a valle dello sfioratore. Per il flusso turbolento, la seguente equazione sarebbe una buona approssimazione per la portata sopra lo sfioratore:

(11)

Qui, è la larghezza del canale e e sono rispettivamente le profondità a monte e a valle.