Abordagem de Conservação de Energia para Análise de Sistemas
Visão Geral
Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Departamento de Engenharia Mecânica, Michigan State University, East Lansing, MI
O objetivo deste experimento é demonstrar a aplicação da equação de conservação de energia para determinar o desempenho de um sistema de fluxo. Para este fim, a equação de energia para fluxo constante e incompressível é aplicada a um tubo curto com uma válvula de portão. A válvula do portão é então gradualmente fechada e sua influência nas condições de fluxo é caracterizada. Além disso, a interação entre este sistema de fluxo e o ventilador que impulsiona o fluxo é estudada comparando a curva do sistema com a curva característica do ventilador.
Este experimento ajuda a entender como a dissipação de energia é usada pelas válvulas para restringir o fluxo. Além disso, sob o mesmo princípio, este experimento oferece um método simples para medir a taxa de fluxo usando a mudança de pressão através de uma entrada afiada.
Princípios
A análise do fluxo de fluidos é frequentemente realizada com base na forma como a energia se transforma à medida que o fluido flui através de um sistema. A energia total transportada por um fluxo inclui energia cinética, potencial e termodinâmica. Essas formas de energia podem se transformar livremente, e a energia contida no fluxo em uma determinada posição em um sistema de fluxo é o equilíbrio entre a energia total de entrada, a energia adicionada e a energia subtraída. Esse equilíbrio energético pode ser expresso na forma de equação da seguinte forma [1, 2]:
 (1)
(1)
Aqui, os subíndices 1 e 5 referem-se às condições de entrada e saída do sistema de fluxo, respectivamente. Figura 2(A) mostra um esquema do sistema de fluxo: o ar entra através de um sistema de escoamento condicionado, ou contração, chamado plenário (sua descarga mostrada na Figura 3(A)). Em seguida, ele transita para um tubo curto com uma válvula no final (ver Figura 2(B) para obter detalhes do sistema de tubulação/válvula, e Figuras 2(A) e (B) para imagens). O ar descarrega da válvula em um espaço fechado isolado do exterior chamado "receptor" (ver Figura 3 para referência). Como mostrado na Figura 3, o receptor é grande o suficiente para abrigar o sistema de aquisição de dados e os experimentalistas. Finalmente, o fluxo sai do receptor através de uma placa perfurada que serve como amortecedor para regulação de fluxo (ver Figura 3(C) para referência). O ar é então capturado por um ventilador centrífuga que descarrega de volta para a atmosfera. Os termos entre parênteses representam o conteúdo energético específico em cada porto, que é a soma de energia potencial  gravitacional, energia cinética
gravitacional, energia cinética 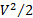 e energia termodinâmica (ou potencial de pressão).
e energia termodinâmica (ou potencial de pressão).  O coeficiente
O coeficiente  é usado para levar em conta a forma do perfil de velocidade. Para o presente experimento
é usado para levar em conta a forma do perfil de velocidade. Para o presente experimento 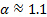 porque o fluxo é turbulento [1, 2]. Como tal, o lado esquerdo da equação (1) representa a mudança no conteúdo energético entre as portas de entrada e saída. Na ausência de trabalho externo ou efeitos dissipativos, essa diferença é zero. No entanto, a maioria das aplicações de engenharia envolvendo fluxos reais incluem adição ou subtração de energia por meio de máquinas de
porque o fluxo é turbulento [1, 2]. Como tal, o lado esquerdo da equação (1) representa a mudança no conteúdo energético entre as portas de entrada e saída. Na ausência de trabalho externo ou efeitos dissipativos, essa diferença é zero. No entanto, a maioria das aplicações de engenharia envolvendo fluxos reais incluem adição ou subtração de energia por meio de máquinas de  fluxo, e efeitos dissipadores,
fluxo, e efeitos dissipadores,  . Estes dois efeitos estão incluídos no lado direito da equação (1).
. Estes dois efeitos estão incluídos no lado direito da equação (1).
Neste experimento, um ventilador centrífuga será usado para induzir o fluxo, ou seja, para adicionar energia ao fluido. Para este tipo de máquina, o termo  é uma função da taxa de fluxo chamada curva característica e é determinada
é uma função da taxa de fluxo chamada curva característica e é determinada  experimentalmente:
experimentalmente:
 (2)
(2)
Aqui, 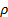 e estão a densidade e
e estão a densidade e  viscosidade cinemática do ar em condições locais, e
viscosidade cinemática do ar em condições locais, e 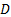 é o diâmetro do sistema de fluxo
é o diâmetro do sistema de fluxo  (mm no presente experimento). A equação (2) é de uma forma que garante que as constantes no primeiro e segundo mandato sejam adimensionais, enquanto a constante no terceiro termo está em unidades de pressão (Pa) para garantir a homogeneidade dimensional. Equação (2) é a "curva de desempenho do ventilador" mostrada na Figura 1.
(mm no presente experimento). A equação (2) é de uma forma que garante que as constantes no primeiro e segundo mandato sejam adimensionais, enquanto a constante no terceiro termo está em unidades de pressão (Pa) para garantir a homogeneidade dimensional. Equação (2) é a "curva de desempenho do ventilador" mostrada na Figura 1.
Finalmente, a dissipação de energia é proporcional à energia cinética do fluxo:
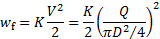 (3)
(3)
Observe que, utilizando a equação de continuidade (  , onde está a área
, onde está a área 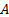 transversal [1, 2]), a dissipação de energia também pode ser escrita em termos da taxa de fluxo,
transversal [1, 2]), a dissipação de energia também pode ser escrita em termos da taxa de fluxo,  . A Figura 1 apresenta esta última forma de equação (3) como a "curva do sistema de fluxo". Na equação (3), o coeficiente de
. A Figura 1 apresenta esta última forma de equação (3) como a "curva do sistema de fluxo". Na equação (3), o coeficiente de  proporcionalidade, é chamado de coeficiente de perda e é a adição de todos os efeitos dissipadores induzidos pelos elementos do sistema de fluxo como resultado de interações viscosas. Enquanto as contribuições de tubos e dutos dependem de sua rugosidade, comprimento e número de Reynolds, a contribuição de conexões de tubulação, entradas e descargas, expansões, contrações, curvas e válvulas depende de suas geometrias particulares. Para o presente experimento, o coeficiente geral de perda é a combinação de uma entrada, uma válvula e uma descarga:
proporcionalidade, é chamado de coeficiente de perda e é a adição de todos os efeitos dissipadores induzidos pelos elementos do sistema de fluxo como resultado de interações viscosas. Enquanto as contribuições de tubos e dutos dependem de sua rugosidade, comprimento e número de Reynolds, a contribuição de conexões de tubulação, entradas e descargas, expansões, contrações, curvas e válvulas depende de suas geometrias particulares. Para o presente experimento, o coeficiente geral de perda é a combinação de uma entrada, uma válvula e uma descarga:
 (4)
(4)
Onde os valores dos coeficientes de perda para a entrada e descarga são 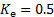
 e, respectivamente, (ver [1, 2] para referência). O coeficiente de perda para a
e, respectivamente, (ver [1, 2] para referência). O coeficiente de perda para a  válvula, será discutido na seção seguinte.
válvula, será discutido na seção seguinte.
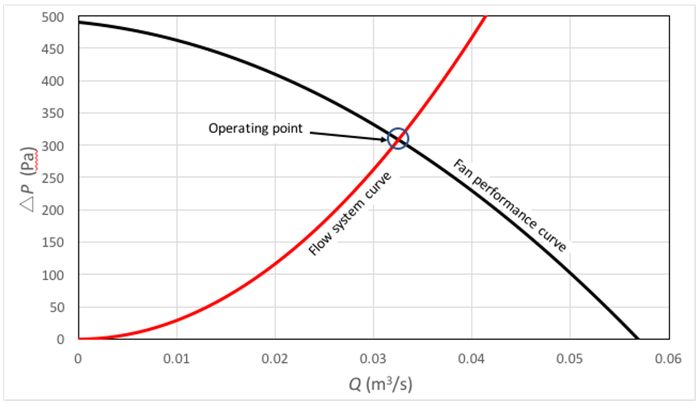
Figura 1. Exemplo de curva do sistema e curva de desempenho do ventilador.  : curva do sistema;
: curva do sistema;  : curva de desempenho do ventilador. O círculo azul destaca a intersecção entre as duas curvas, que é o ponto de operação.
: curva de desempenho do ventilador. O círculo azul destaca a intersecção entre as duas curvas, que é o ponto de operação.

Figura 2. Configuração experimental. (A): Facilidade de fluxo. O fluxo se move da esquerda para a direita; entra no plenário através de uma seção de condicionamento de fluxo, depois flui através do tubo e da válvula, descarrega dentro do receptor e finalmente sai do sistema através do ventilador. (B): Detalhes do sistema de fluxo e equipamentos de aquisição de dados. Clique aqui para ver uma versão maior desta figura.

Figura 3. Sistema de aquisição de dados. (A) As conexões desses dispositivos de aquisição de dados seguem o diagrama na Figura 2(B). (B) Interface virtual para aquisição de dados (escrita no LabView). Clique aqui para ver uma versão maior desta figura.
Características de dissipação de uma válvula
Uma vez que as válvulas são essencialmente dispositivos de geometria variável, seu coeficiente de perda específico é uma função do ângulo de rotação de seu eixo (  ). Com isso em mente,
). Com isso em mente, 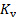 varia conforme a válvula é aberta ou fechada de acordo com a seguinte relação:
varia conforme a válvula é aberta ou fechada de acordo com a seguinte relação:
 (5)
(5)
Aqui, usamos novamente a equação de continuidade para expressar o coeficiente de perdas em termos da taxa de fluxo. Além disso, a equação (5) sugere que podemos determinar o coeficiente de perda para a válvula sabendo o valor da taxa de fluxo e a queda de pressão através da válvula em função do ângulo de abertura e da taxa de fluxo:  . Essa também é a diferença de pressão entre os pontos 3 e 4 na Figura 2(B) (
. Essa também é a diferença de pressão entre os pontos 3 e 4 na Figura 2(B) (  ).
).
Ponto de operação
Como mostrado na Figura 1, o Ponto de Operação de um sistema de fluxo impulsionado por uma máquina de fluxo, como o apresentado neste experimento, é dado pelo ponto de intersecção da curva característica do ventilador e da curva fluxo-sistema. Este ponto pode ser caracterizado usando a equação de energia da seguinte forma: como pode ser visto na Figura 2(A), o ar entra no sistema de fluxo a partir de uma grande sala em condições atmosféricas e sai para a mesma sala sem qualquer mudança significativa de altura. Em consequência, as condições de pressão, velocidade e altura na entrada e saída do sistema 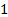 (e
(e  subíndices na equação (1) respectivamente) são idênticas e se cancelam. Consequentemente, a energia adicionada pelo ventilador é equilibrada pela energia dissipada pelo sistema de fluxo. Em outras palavras, as equações (2) e (3) formam uma igualdade que resulta na seguinte relação após a simplificação:
subíndices na equação (1) respectivamente) são idênticas e se cancelam. Consequentemente, a energia adicionada pelo ventilador é equilibrada pela energia dissipada pelo sistema de fluxo. Em outras palavras, as equações (2) e (3) formam uma igualdade que resulta na seguinte relação após a simplificação:
 (6)
(6)
A raiz positiva desta equação expressa o Ponto Operacional:
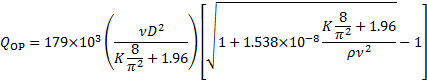 (7)
(7)
Aqui, o subíndice "OP" significa "Ponto Operacional". O coeficiente de perda na equação (7) é a adição dos coeficientes de perda da entrada, válvula e descarga. Das equações (4) e (5):
 (8)
(8)
Medição da taxa de fluxo
Análogo a todas as análises anteriores, a equação (1) é aplicada entre o plenário e um ponto a jusante da entrada afiada (pontos 2 e 3 na figura 2(B)) para recuperar a seguinte equação:
 (9)
(9)
Aqui, usamos o fato de que não há mudança de altura entre os pontos 2 e 3, e a velocidade dentro do plenário é insignificante. Introduzindo a equação de continuidade ( 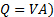 e equação (3), chegamos à seguinte relação para a taxa de fluxo em termos da diferença de pressão entre o plenário (ponto 2 na Figura 2(B)) e a pressão estática a montante da válvula (ponto 3 na Figura 2(B)):
e equação (3), chegamos à seguinte relação para a taxa de fluxo em termos da diferença de pressão entre o plenário (ponto 2 na Figura 2(B)) e a pressão estática a montante da válvula (ponto 3 na Figura 2(B)):
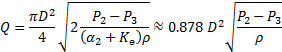 (10)
(10)
O constante 0,878 é obtido após substituir os valores do coeficiente de perda e correção de velocidade ( 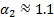
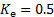 e, ver [1, 2] para referência) e agrupar todas as constantes em uma única.
e, ver [1, 2] para referência) e agrupar todas as constantes em uma única.
Procedimento
1. Definindo a instalação
- Certifique-se de que o ventilador não está funcionando, para que não haja fluxo na instalação.
- Verifique se o sistema de aquisição de dados (Figura 4(A)) segue o esquema na figura 2B.
- Conecte a porta positiva do transdutor de pressão #1 (ver figura 2B para referência) à torneira de pressão a montante da válvula (
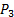 ).
). - Deixe a porta negativa do transdutor de pressão #1 aberta às condições do quarto (receptor:
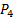 ). Assim, a leitura deste transdutor será
). Assim, a leitura deste transdutor será  diretamente.
diretamente. - Conecte a porta positiva do transdutor de pressão #2 (ver figura 2B para referência) à torneira de pressão do plenário (
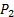 ).
). - Conecte a porta negativa do transdutor de pressão #2 (ver figura 2B para referência) à torneira de pressão a montante da válvula (
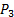 ). Assim, a leitura deste transdutor será
). Assim, a leitura deste transdutor será  diretamente, conforme exigido pela equação (10).
diretamente, conforme exigido pela equação (10).
- Conecte a porta positiva do transdutor de pressão #1 (ver figura 2B para referência) à torneira de pressão a montante da válvula (
- Certifique-se de que o canal virtual 0 no sistema de aquisição de dados (Figura 4(B)) corresponde a #1 transdutor de pressão
 ( ) e o canal virtual 1 corresponde a #2 transdutor de pressão (
( ) e o canal virtual 1 corresponde a #2 transdutor de pressão (  ).
). - Defina o sistema de aquisição de dados para amostrar a uma taxa de 100 Hz para um total de 500 amostras (ou seja, 5s de dados).
Mesa 1. Parâmetros básicos para estudo experimental.
|
Parâmetro |
Valor |
| Diâmetro do tubo(D) | 50,8 mm (2 polegadas) |
| Constante de calibração de #1 transdutor (m_p1) |
|
| Constante de calibração #2 transdutor (m_p2) |
|
| Pressão atmosférica local | 100.474,15 Pa |
| Temperatura local | 297,15 K |
| Densidade do ar local | 1.186 kg/m3 |

Figura 4. Instalações de fluxo. (A): vista da descarga do plenário na seção receptora antes de instalar o conjunto de válvulas a serem estudadas. (B): três tipos diferentes de válvulas dentro do receptor. Da esquerda para a direita: válvula de portal, válvula globo, válvula borboleta. (C): portas de saída do receptor. As válvulas descarregam o fluxo dentro do receptor, e o ventilador suga o fluxo do receptor através da placa perfurada na imagem. Clique aqui para ver uma versão maior desta figura.
2. Medições
- Regissuço o diâmetro do tubo conectado à válvula e calcule sua área transversal.
- Determine o número máximo de voltas completas da alça necessária para mover a válvula da posição totalmente fechada para a posição totalmente aberta. Se esse número não for um inteiro, exclua a última rotação fracionada para simplificar esta análise. Para o experimento atual, o número máximo de curvas completas é de 12.
- Feche a válvula completamente.
- Gire a pega da válvula até que ela esteja totalmente aberta enquanto conta o número de curvas completas. Para simplificar, use apenas um número inteiro de voltas para o experimento. Por exemplo, são necessárias aproximadamente 12 voltas e 1/3 de uma curva para abrir totalmente a válvula usada neste experimento. Assim, vamos girar a alça desta válvula apenas 12 voltas completas a partir de sua posição totalmente fechada e definir isso como a posição inicial (
 ).
). - Ligue a instalação de fluxo.
- Use o sistema de aquisição de dados para registrar as leituras
 de e
de e  .
. - Digite na tabela 2 os valores médios e obtidos com o sistema de aquisição de

 dados.
dados. - Feche a válvula em 1,5 voltas.
- Repita as etapas 2.6 a 2.8 até que a tabela 2 esteja totalmente povoada.
- Desligue a instalação de fluxo.
3. Análise de dados
- Determine o coeficiente de perda da válvula para cada posição angular usando equação (5). Digite esses valores na tabela 2.
- Determine a taxa de fluxo para cada posição angular da válvula usando equação (10). Digite esses valores na tabela 2.
- Determine o ponto de operação usando a equação (7). Digite esses valores na tabela 2.
- Calcule a diferença relativa entre a taxa de fluxo medida e o ponto de operação
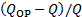
- Use a equação (3) para produzir um gráfico das curvas do sistema para todos os valores de
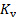 . Considere o coeficiente de perda total como
. Considere o coeficiente de perda total como  .
. - Adicione a curva característica do ventilador a esta mesma trama usando equação (2).
Mesa 2. Resultados representativos. Medições de diferenças de pressão e estimativas de taxa de fluxo e coeficientes de perda.
| [P_pl-P_a] (Pa) | [P_a-P_r] (Pa) | Q (m3/s) | K | Q_OP (m3/s) | ε |
| 246.75 | 54.00 | 0.0327 | 0.450 | 0.0316 | -3.16 |
| 208.62 | 114.22 | 0.0301 | 0.976 | 0.0293 | -2.51 |
| 156.19 | 204.80 | 0.0260 | 2.198 | 0.0254 | -2.30 |
| 109.30 | 281.69 | 0.0218 | 4.224 | 0.0214 | -1.53 |
| 71.82 | 348.38 | 0.0176 | 7.863 | 0.0174 | -1.26 |
| 38.72 | 408.60 | 0.0129 | 16.989 | 0.0128 | -0.90 |
| 15.00 | 452.39 | 0.0081 | 48.359 | 0.0080 | -0.32 |
| 2.51 | 482.50 | 0.0033 | 307.799 | 0.0033 | -0.18 |
Resultados
A Figura 5 mostra os resultados das medições atuais. Aqui, a linha sólida preta foi gerada com equação (2), e cada linha vermelha com equação (3) para diferentes valores do coeficiente de perda da válvula. A partir da figura, é evidente que a curva do sistema aumenta sua inclinação à medida que a válvula se fecha. Em outras palavras, este experimento demonstra que o princípio por trás do funcionamento de uma válvula é aumentar a dissipação de energia para restringir o fluxo. Por outro lado, a partir da equação (5), pode-se inferir que o valor de 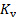 se torna infinito quando a válvula está totalmente fechada. Conceitualmente, essa condição significa que toda a energia é dissipada, portanto, impedindo completamente o fluxo através da válvula.
se torna infinito quando a válvula está totalmente fechada. Conceitualmente, essa condição significa que toda a energia é dissipada, portanto, impedindo completamente o fluxo através da válvula.
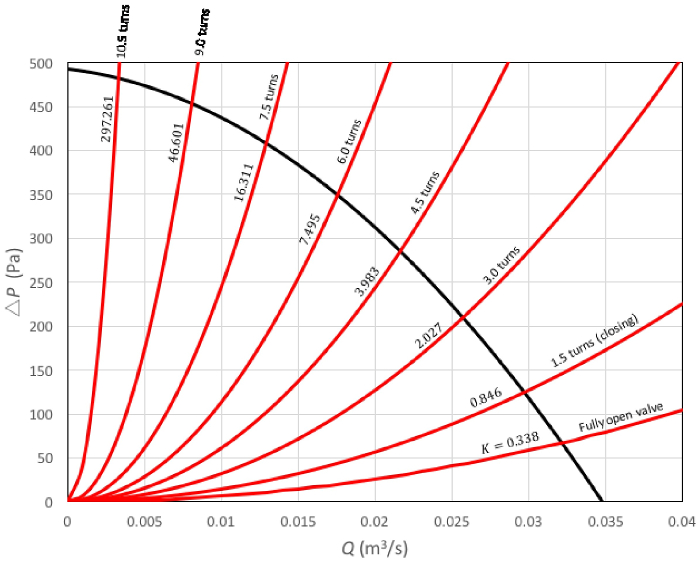
Figura 5. Resultados representativos.  : curvas do sistema. Cada curva nesta família é o resultado de um grau diferente de abertura da válvula. A inclinação das curvas aumenta à medida que a válvula é fechada. Cada curva tem seu coeficiente de perda correspondente para referência;
: curvas do sistema. Cada curva nesta família é o resultado de um grau diferente de abertura da válvula. A inclinação das curvas aumenta à medida que a válvula é fechada. Cada curva tem seu coeficiente de perda correspondente para referência;  : curva de desempenho do ventilador. Clique aqui para ver uma versão maior desta figura.
: curva de desempenho do ventilador. Clique aqui para ver uma versão maior desta figura.
Como mostrado na Tabela 2, o erro entre a taxa de fluxo estimada no ponto de operação (equação (7)) e a taxa de fluxo medida (equação (10)) permanece abaixo de 3,2% para a faixa estudada de taxas de fluxo. Embora este seja um resultado satisfatório dado o pequeno erro percentual, a taxa de fluxo estimada no ponto de operação é sempre subestimada, e segue uma tendência de diminuição à medida que a válvula é gradualmente fechada. Essa tendência oferece alguma visão sobre o comportamento do sistema de fluxo, particularmente porque o valor do fator de correção para a não uniformidade da velocidade aumenta ligeiramente com o  número de Reynolds. Não surpreende, portanto, que o erro aumente com a taxa de fluxo.
número de Reynolds. Não surpreende, portanto, que o erro aumente com a taxa de fluxo.
Aplicação e Resumo
Este experimento explorou a aplicação da equação de energia para caracterizar a ação de uma válvula no fluxo do tubo. Observou-se que a válvula induz a resistência ao fluxo aumentando a dissipação de energia. Considerando que a queda de pressão ao longo do sistema de fluxo é diretamente proporcional ao quadrado da taxa de fluxo, o efeito da dissipação de energia é capturado pela magnitude do coeficiente de proporcionalidade. Este coeficiente é a adição dos coeficientes de perda de todos os elementos do sistema de fluxo, incluindo a válvula. O coeficiente de perda da válvula aumenta monotonicamente à medida que a válvula é gradualmente fechada. E esse efeito aumenta a inclinação da curva do sistema como resultado, atingindo um valor de infinito quando a válvula está totalmente fechada.
O comportamento acima descrito foi contrastado com a curva de desempenho do ventilador centrífuga que impulsiona o fluxo. Ao comparar a taxa de fluxo medida diretamente com a taxa de fluxo estimada pela intersecção da curva do sistema e a curva de desempenho do ventilador, foi demonstrado que este ponto de intersecção define as condições operacionais de vazão e demanda de pressão.
Este experimento serviu com o propósito de demonstrar os princípios da conservação de energia para caracterizar algumas aplicações de engenharia diferentes: operação da válvula, medição da taxa de fluxo e condições operacionais de um sistema de fluxo. A conservação de energia pode ser usada basicamente para caracterizar qualquer sistema de fluxo, estes são mais dois exemplos de aplicações da equação energética:
A energia cinética transportada pelo vento pode ser colhida por turbinas eólicas para produzir energia elétrica. Comparando a montante com as condições de fluxo a jusante, a equação de energia pode ser usada para avaliar quanta energia foi removida do vento. A magnitude da energia recuperada será dada pelo trabalho do eixo,  na equação (1).
na equação (1).
A mudança na energia potencial gravitacional pode ser usada para avaliar a vazão da água sobre um vertedouro. Isso é feito em combinação com a equação de conservação de massa medindo as profundezas rio acima e rio abaixo do vertedouro. Para o fluxo turbulento, a seguinte equação seria uma boa aproximação para a taxa de fluxo sobre o vertedouro:
 (11)
(11)
Aqui,  é a largura do canal e são as
é a largura do canal e são as 
 profundidades rio acima e rio abaixo, respectivamente.
profundidades rio acima e rio abaixo, respectivamente.
Referências
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
Tags
Pular para...
Vídeos desta coleção:

Now Playing
Abordagem de Conservação de Energia para Análise de Sistemas
Mechanical Engineering
7.4K Visualizações

Empuxo e Arrasto em Corpos Imersos
Mechanical Engineering
29.9K Visualizações

Estabilidade de Embarcações Flutuantes
Mechanical Engineering
22.4K Visualizações

Propulsão e Impulso
Mechanical Engineering
21.6K Visualizações

Redes de tubulação e perdas de pressão
Mechanical Engineering
58.1K Visualizações

Resfriamento e Ebulição
Mechanical Engineering
7.7K Visualizações

Saltos Hidráulicos
Mechanical Engineering
40.9K Visualizações

Análise de Trocadores de Calor
Mechanical Engineering
28.0K Visualizações

Introdução à Refrigeração
Mechanical Engineering
24.7K Visualizações

Anemometria com fio quente
Mechanical Engineering
15.5K Visualizações

Medindo fluxos turbulentos
Mechanical Engineering
13.5K Visualizações

Visualização do Fluxo ao Redor de um Corpo Parado
Mechanical Engineering
11.8K Visualizações

Jato Incidindo em uma Placa Inclinada
Mechanical Engineering
10.7K Visualizações

Conservação de Massa e Medições de Taxa de Fluxo
Mechanical Engineering
22.6K Visualizações

Determinação das Forças de Impacto em uma Placa Plana com o Método do Volume de Controle
Mechanical Engineering
26.0K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados