Stabilità dei vasi galleggianti
Panoramica
Fonte: Alexander S Rattner e Kevin Rao Li Dipartimento di Ingegneria Meccanica e Nucleare, The Pennsylvania State University, University Park, PA
L'obiettivo di questo esperimento è dimostrare il fenomeno della stabilità delle navi galleggianti - la capacità di auto-destra quando vengono ribaltate di lato da una forza esterna. Un'attenta progettazione delle forme dello scafo e della distribuzione interna della massa consente alle navi marittime di essere stabili con bassi pescaggio (profondità sommersa dello scafo), migliorando la manovrabilità della nave e riducendo la resistenza.
In questo esperimento, un modello di barca verrà prima modificato per consentire la regolazione del suo centro di massa (che rappresenta diversi carichi di carico) e il tracciamento automatico del suo angolo di rollio. La barca sarà collocata in un contenitore d'acqua e inclinata a diverse angolazioni con altezze variabili del suo centro di massa. Una volta rilasciato, il capovolgimento (ribaltamento) o il movimento oscillante della barca saranno tracciati con una fotocamera digitale e un software di analisi video. I risultati per l'angolo di rollio massimo stabile e la frequenza di oscillazione saranno confrontati con i valori teorici. I calcoli di stabilità verranno eseguiti utilizzando le proprietà geometriche e strutturali della barca determinate in un ambiente di progettazione assistita da computer.
Principi
La forza di galleggiamento, che sostiene le navi galleggianti, è uguale al peso del fluido spostato dalla parte sommersa di tali navi. La forza di galleggiamento agisce verso l'alto, lungo la linea verticale che passa attraverso il centroide (centro del volume) di questo volume sommerso. Questo punto è chiamato il centro di galleggiamento. Se il centro di massa di una struttura galleggiante è al di sotto del suo centro di galleggiamento, qualsiasi rotolamento laterale (movimentodi sbandamento) impartirà un momento per raddrizzare la struttura, riportandola all'orientamento verticale (Fig. 1a). Se il centro di massa è sopra il centro di galleggiamento, la struttura potrebbe essere instabile, causando il capovolgimento se disturbata (Fig. 1b). Tuttavia, se lo scafo di una nave galleggiante è progettato con attenzione, può essere stabile, anche se il suo centro di massa è sopra il suo centro di galleggiamento. Qui, ribaltare leggermente la nave fa cambiare leggermente la forma del suo volume sommerso, spostando il suo centro di galleggiamento verso l'esterno nella direzione del ribaltamento. Ciò si traduce in un momento di raddrizzamento netto fintanto che la linea d'azione di galleggiamento è al di fuori del centro di massa della struttura (Fig. 1c). Equivalentemente, una nave sarà stabile se il punto di intersezione della linea d'azione di galleggiamento e la linea centrale dello scafo (metacentro) è al di sopra del suo centro di massa. Alcune navi sono metastabili - solo auto-raddrizzanti fino a qualche angolo critico.
È anche importante considerare il comportamento dinamico di una nave galleggiante. Forti impulsi dalle onde possono far ruotare una barca oltre il suo limite metastabile, anche se l'angolo di ribaltamento iniziale è piccolo(cioè, 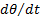 grande per piccolo
grande per piccolo  ). La frequenza e l'ampiezza dell'oscillazione possono anche influire sul comfort dei passeggeri. Il movimento rottorio di una nave può essere previsto con un equilibrio momentaneo attorno al suo centro di massa. Qui, Izz è il momento di inerzia intorno al centro di massa, θ è l'angolo di rollio, m è la massa del vaso e Lcm,mc è la distanza lungo la linea mediana della barca dal suo centro di massa al suo metacentro.
). La frequenza e l'ampiezza dell'oscillazione possono anche influire sul comfort dei passeggeri. Il movimento rottorio di una nave può essere previsto con un equilibrio momentaneo attorno al suo centro di massa. Qui, Izz è il momento di inerzia intorno al centro di massa, θ è l'angolo di rollio, m è la massa del vaso e Lcm,mc è la distanza lungo la linea mediana della barca dal suo centro di massa al suo metacentro.
 (1)
(1)

Figura 1: a. Nave stabile con centro di massa al di sotto del centro di galleggiamento, garantendo il momento di raddrizzamento. b. Nave instabile con centro di massa sopra il centro di galleggiamento. c. Forma dello scafo che fa sì che il centro di galleggiamento agisca al di fuori del centro di massa (metacentro sopra il centro di massa). Ciò produce stabilità anche con il centro di massa sopra il centro di galleggiamento.
Procedura
1. Misurare l'angolo massimo di stabilità
- Seleziona un piccolo modello di barca. Si raccomanda un design dello scafo relativamente semplice per ridurre la complessità dell'analisi nelle sezioni 3 e 4.
- Collegare un albero verticale leggero dai colori vivaci alla barca (blu consigliato). Il codice MATLAB fornito tiene traccia della posizione dell'albero nel video cercando pixel blu brillante nell'immagine. Se si utilizza un albero di colore diverso, il codice di analisi dell'immagine dovrà essere regolato di conseguenza.
- Fissare comodamente una fascetta all'albero per fungere da arresto per un peso. Far scorrere un peso(ad esempio, dado di accoppiamento) sull'albero in modo che si appoggi sull'arresto.
- Metti la barca in un contenitore d'acqua più grande e lasciala depositare (Fig. 2a). Posizionare la configurazione in modo che il flusso d'aria nella stanza non disturbi la barca. Montare una videocamera rivolta verso l'albero lungo la lunghezza della barca. Si consiglia uno sfondo bianco.
- Raccogli un video di riferimento della barca a riposo e analizzalo utilizzando la funzione MATLAB fornita (TrackMast.m). Regolare l'orientamento della fotocamera fino a quando non legge correttamente l'inclinazione 0 quando la barca è a riposo. Potrebbe essere necessario regolare i parametri di mascheramento per isolare l'albero sulla riga 17 del codice.
- Raccogli video di ribaltamento molto graduale della barca premendo lateralmente sulla parte superiore dell'albero fino a quando non cade da sola (si capovolge). Mantenere l'albero nel fotogramma video il più a lungo possibile durante ogni test. Eseguire questa procedura per diverse altezze del peso. Registrare l'altezza del peso sull'albero per ogni caso.
- Analizza questi video utilizzando lo script MATLAB fornito. Per ogni caso, l'angolo massimo stabile può essere determinato mediante l'ispezione dell'angolo di uscita e delle matrici temporali. Completa una tabella dell'angolo di capovolgimento rispetto all'altezza del peso.
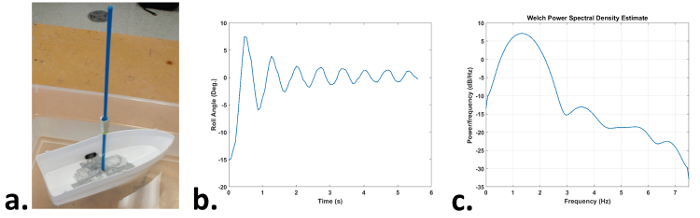
Figura 2: a. Modello di barca con peso regolabile sull'albero, b. Variazione dell'angolo di rollio con quando rilasciato da un angolo leggero (passo 2.1), c. Grafico della densità dello spettro di potenza di (b) che mostra la frequenza di oscillazione del picco di 1,4 Hz Fare clic qui per visualizzare una versione più grande di questa figura.
2. Misurare la frequenza di oscillazione
- Esegui una seconda serie di esperimenti di ribaltamento con due diverse altezze di peso dell'albero. Questa volta, punta solo leggermente la barca (~ 10 °) e raccogli video della barca a dondolo per 10 - 15 s.
- Eseguire nuovamente la funzione di tracciamento dell'albero sul video. Dopo aver chiamato la funzione, valutare la seguente espressione MATLAB sull'output: pwelch( theta,[],[], [],1/(t(2)-t(1)) ); . Questo trastricerà la densità dello spettro di potenza per la barca a dondolo. La frequenza di rotolamento primaria è il valore di picco su questo grafico (Fig. 2b-c).
3. Previsione dell'angolo di ribaltamento
- Utilizzando una bilancia, misurare la massa della barca modello, compreso l'albero e il peso.
- Per ogni posizione del peso dell'albero valutata nel passaggio 1.5, bilanciare la barca su un lato con l'albero su un bordo dritto. Registrare l'altezza del punto di equilibrio dal fondo dello scafo come centro di massa (Hcm).
- Utilizzando un pacchetto software CAD, creare un modello in scala della barca e dell'albero con il peso. Assicurarsi che lo scafo sia riempito (solido) in questo modello (Fig. 3a).
- Posizionare il modello in modo che la linea centrale dello scafo inferiore (chiglia) coincida con l'origine nell'ambiente CAD e l'albero sia (inizialmente) parallelo all'asse verticale (y).
- Nell'ambiente CAD, ruotare la barca attorno all'asse z, che si trova lungo la lunghezza dello scafo, con piccoli incrementi (ad esempio, 5°, 10°, 15°...).
- Dopo ogni rotazione, tagliare via tutta la barca sopra un livello verticale in modo tale che il volume della porzione inferiore rimanente sia uguale alla massa totale della barca divisa per la densità dell'acqua (m / ρw, ρw = 1000 kg m-3). Questo rappresenta la porzione della barca sotto la linea di galleggiamento quando galleggia con quell'angolo (Fig. 3b).
- Utilizzando la funzione "Mass Properties" nel software CAD, valutare la posizione x del centroide dello scafo rimanente. Qui, l'origine dovrebbe essere lungo il bordo più basso del boal (la chiglia) e l'asse x dovrebbe puntare nella direzione orizzontale. Questo rappresenta il centro di galleggiamento (xb); la forza di galleggiamento agisce attraverso questo punto. Preparare una tabella di xcm vs. θ.
- Per ogni angolo massimo stabile (θ) identificato nel passo 1.6, confrontare il braccio momento del peso della barca (
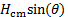 ) e il braccio momento della forza di galleggiamento di ripristino (
) e il braccio momento della forza di galleggiamento di ripristino ( 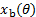 ). Potrebbe essere necessario interpolare tra i valori ottenuti nel passaggio 3.7. Questi si bilanciano approssimativamente?
). Potrebbe essere necessario interpolare tra i valori ottenuti nel passaggio 3.7. Questi si bilanciano approssimativamente?
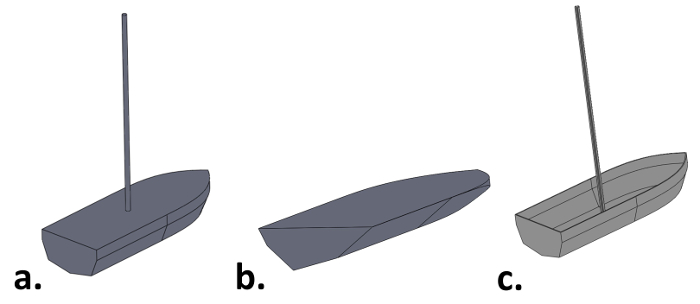
Figura 3: a. Modello compilato dello scafo della barca, b. Taglio verticale dello scafo, che rivela il volume sommerso della nave, c. Modello fisicamente accurato della nave.
4. Prevedere il periodo di oscillazione
- Produrre un secondo modello CAD della barca con la posizione del peso corrispondente ai casi di cui al punto 2.1. Questa volta modella lo spessore effettivo dello scafo(cioè, non riempito, Fig. 3c). Abbinare la densità dei materiali con i valori effettivi.
- Utilizzando la funzione "Mass Properties" del software CAD, valutare il momento di inerzia della barca intorno al suo centro di massa lungo l'asse dirollio( Izz) per le altezze di peso.
- Utilizzando i risultati dei passi precedenti e la posizione xdel centro di galleggiamento misurata quando
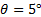 (passo 3.7), valutare le frequenze di oscillazione teoriche:
(passo 3.7), valutare le frequenze di oscillazione teoriche: (2)
(2) - Confrontare il risultato teorico del passo 4.3 con le frequenze di oscillazione misurate. Questi valori concordano ragionevolmente bene?
Risultati
| Massa totale (m, kg) |
Centro di massa (Hcm, m) |
Centro di galleggiamento (  , m) , m)
|
Momento di inerzia (Izz, kg m2) |
| 0.088 (Passo 3.1) |
0.053 (Passo 3.2) |
0.0078 (Passo 3.7) |
0.00052 (Passo 4.2) |
Tabella 1. Proprietà del modello di barca con peso di 24 g posizionata a 13 cm sopra la chiglia.
| Fase della procedura | Valore sperimentale | Valore previsto |
| Angolo massimo di rollio stabile (1.6, 3.8) | ~25° | 28,5° |
| Frequenza naturale del rotolo (2.2, 4.3) | 1,4 Hz | 1,24 Hz |
Tabella 2. Angolo di rollio massimo stabile e frequenza di rotolamento della barca con peso di 24 g 13 cm sopra la chiglia.
Applicazione e Riepilogo
Questo esperimento ha dimostrato i fenomeni di stabilità delle navi galleggianti e come le navi possono rimanere in posizione verticale anche con centri di massa relativamente alti. Ad esempio, nei risultati rappresentativi, un piccolo modello di barca con un centro di massa(Hcm = 5,3 cm) ben al di sopra della linea di galleggiamento(linea d'acqua H~ 1 - 2 cm) potrebbe tornare alla sua posizione verticale dopo essere stato inclinato ad un angolo di ~ 25 °. Negli esperimenti, è stato misurato l'angolo massimo stabile per un modello di barca con diversi centri verticali di massa. È stato anche valutato l'effetto dell'altezza del centro di massa sulla frequenza di oscillazione (rotolamento). Entrambe queste misurazioni sono state confrontate con i valori teorici ottenuti utilizzando parametri geometrici in pacchetti CAD. Questi risultati e procedure possono servire come punto di partenza per gli studenti che cercano di progettare e analizzare strutture galleggianti.
La proprietà di stabilità è cruciale per la progettazione e il funzionamento delle navi marittime. Le navi che operano con correnti d'aria poco profonde (la maggior parte delle navi sopra l'acqua) hanno una resistenza ridotta e una maggiore manovrabilità. Nelle grandi navi da carico, i container di spedizione possono essere impilati in alto sopra il ponte superiore, aumentando la capacità di carico e facilitando le operazioni di carico e scarico. Nelle navi da crociera, le correnti d'aria poco profonde consentono molte finestre e ponti per i passeggeri. Mentre la stabilità è fondamentale per la sicurezza, le forme dello scafo molto stabili  (alte) producono frequenze di oscillamento veloci (Eqn. 2), che possono essere scomodamente scattanti per i passeggeri. Le analisi di stabilità idrostatica, come dimostrato in questo esperimento, sono quindi strumenti cruciali per guidare l'ingegneria marina.
(alte) producono frequenze di oscillamento veloci (Eqn. 2), che possono essere scomodamente scattanti per i passeggeri. Le analisi di stabilità idrostatica, come dimostrato in questo esperimento, sono quindi strumenti cruciali per guidare l'ingegneria marina.
Tags
Vai a...
Video da questa raccolta:

Now Playing
Stabilità dei vasi galleggianti
Mechanical Engineering
23.2K Visualizzazioni

Galleggiabilità e trascinamento su corpi immersi
Mechanical Engineering
30.2K Visualizzazioni

Propulsione e spinta
Mechanical Engineering
22.1K Visualizzazioni

Reti di tubazioni e perdite di carico
Mechanical Engineering
58.8K Visualizzazioni

Raffreddamento ed ebollizione
Mechanical Engineering
8.2K Visualizzazioni

Salti idraulici
Mechanical Engineering
41.3K Visualizzazioni

Analisi dello scambiatore di calore
Mechanical Engineering
28.3K Visualizzazioni

Introduzione alla refrigerazione
Mechanical Engineering
25.0K Visualizzazioni

Anemometria a filo caldo
Mechanical Engineering
15.9K Visualizzazioni

Misurazione di flussi turbolenti
Mechanical Engineering
13.6K Visualizzazioni

Visualizzazione del flusso oltre un corpo Bluff
Mechanical Engineering
12.2K Visualizzazioni

Getto che incide su una piastra inclinata
Mechanical Engineering
10.8K Visualizzazioni

Conservazione dell'energia come approccio all'analisi del sistema
Mechanical Engineering
7.4K Visualizzazioni

Conservazione di massa e misure di portata
Mechanical Engineering
22.9K Visualizzazioni

Determinazione delle forze di impingement su una piastra piana con il metodo del volume di controllo
Mechanical Engineering
26.0K Visualizzazioni