שימור הגישה האנרגטית לניתוח מערכות
Overview
מקור: ריקרדו מג'יה-אלווארז וחוסאם היקמט ג'באר, המחלקה להנדסת מכונות, אוניברסיטת מדינת מישיגן, מזרח לנסינג, MI
מטרת הניסוי היא להדגים את היישום של משוואת שימור האנרגיה כדי לקבוע את הביצועים של מערכת זרימה. כדי כך, משוואת האנרגיה לזרימה יציבה ובלתי ניתנת לריסון מוחלת על צינור קצר עם שסתום שער. שסתום השער נסגר בהדרגה והשפעתו על תנאי הזרימה מאופיינת. בנוסף, יחסי הגומלין בין מערכת זרימה זו לבין המאוורר המניע את הזרימה נחקרים על ידי השוואת עקומת המערכת עם העקומה האופיינית של המאוורר.
ניסוי זה מסייע בהבנת האופן שבו נעשה שימוש בזרימת אנרגיה על ידי שסתומים להגבלת הזרימה. כמו כן, תחת אותו עיקרון, ניסוי זה מציע שיטה פשוטה למדידת קצב הזרימה באמצעות שינוי הלחץ על פני כניסה חדה.
Principles
ניתוח זרימת נוזלים מתבצע לעתים קרובות בהתבסס על האופן שבו אנרגיה משתנה כאשר הנוזל זורם דרך מערכת. האנרגיה הכוללת הנישאת זרימה כוללת אנרגיה קינטית, פוטנציאלית ותרמודינמית. צורות אנרגיה אלה עשויות להפוך זו לזו בחופשיות, והאנרגיה הכלולה בזרימה במיקום נתון במערכת זרימה היא האיזון בין סך האנרגיה הנכנסת, האנרגיה הנוספת והאנרגיה המופחתת. מאזן אנרגיה זה יכול לבוא לידי ביטוי בצורת משוואה באופן הבא [1, 2]:
 (1)
(1)
כאן, תת-1 ו- 5 מתייחסים לתנאי המפרצון והשקע של מערכת הזרימה בהתאמה. איור 2(A) מציג סכמטי של מערכת הזרימה: האוויר נכנס דרך מערכת מיזוג זרימה, או התכווצות הנקראת מליאה (פריקתו מוצגת באיור 3(A)). לאחר מכן, הוא עובר לצינור קצר עם שסתום בקצהו (ראה איור 2(B) לקבלת פרטים על מערכת הצינור/שסתום, ואיורים 2(A) ו-(B) לתמונות). האוויר פולש מהשסתום לחלל סגור המבודד מבחוץ הנקרא "מקלט" (ראו איור 3 לעיון). כפי שניתן לראות באיור 3, המקלט גדול מספיק כדי לשכן את מערכת רכישת הנתונים ואת הניסויים. לבסוף, הזרימה יוצאת מהמקלט דרך צלחת מחוררת המשמשת כמדכאת לוויסות הזרימה (ראו איור 3(ג) לעיון). לאחר מכן נלכד האוויר על ידי מאוורר צנטריפוגלי המשתחרר חזרה לאטמוספירה. המונחים בין סוגריים מייצגים את תוכן האנרגיה הספציפי בכל יציאה, שהוא סכום האנרגיה הפוטנציאלית הכבידתית  , אנרגיה קינטית
, אנרגיה קינטית 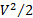 , ואנרגיה תרמודינמית (או פוטנציאל לחץ).
, ואנרגיה תרמודינמית (או פוטנציאל לחץ).  המקדם
המקדם  משמש כדי לקחת בחשבון את הצורה של פרופיל המהירות. לניסוי
משמש כדי לקחת בחשבון את הצורה של פרופיל המהירות. לניסוי 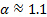 הנוכחי, משום שהזרימה סוערת [1, 2]. ככזה, הצד השמאלי של המשוואה (1) מייצג את השינוי בתוכן האנרגיה בין יציאות הכניסה ליציאה. בהיעדר עבודה חיצונית או השפעות מתפזרות, הבדל זה הוא אפס. עם זאת, רוב היישומים ההנדסיים המערבים זרימות אמיתיות כוללים חיבור או חיסור של אנרגיה באמצעות מכונות זרימה,
הנוכחי, משום שהזרימה סוערת [1, 2]. ככזה, הצד השמאלי של המשוואה (1) מייצג את השינוי בתוכן האנרגיה בין יציאות הכניסה ליציאה. בהיעדר עבודה חיצונית או השפעות מתפזרות, הבדל זה הוא אפס. עם זאת, רוב היישומים ההנדסיים המערבים זרימות אמיתיות כוללים חיבור או חיסור של אנרגיה באמצעות מכונות זרימה,  , ואפקטים מתפזרים,
, ואפקטים מתפזרים,  . שני אפקטים אלה נכללים בצד ימין של המשוואה (1).
. שני אפקטים אלה נכללים בצד ימין של המשוואה (1).
בניסוי זה, מאוורר צנטריפוגלי ישמש כדי לגרום לזרימה, כלומר, כדי להוסיף אנרגיה לנוזל. עבור סוג זה של מכונה, המונח  הוא פונקציה של קצב הזרימה
הוא פונקציה של קצב הזרימה  הנקרא עקומת אופיינית ונקבע באופן ניסיוני:
הנקרא עקומת אופיינית ונקבע באופן ניסיוני:
 (2)
(2)
הנה, 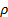
 והם הצפיפות והצמיגות הקינטמטית של האוויר בתנאים מקומיים,
והם הצפיפות והצמיגות הקינטמטית של האוויר בתנאים מקומיים, 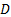 והוא הקוטר של מערכת הזרימה (
והוא הקוטר של מערכת הזרימה (  מ"מ בניסוי הנוכחי). המשוואה (2) היא בצורה המבטאת שהקבועים בקדנציה הראשונה והשנייה הם חסרי ממדים, בעוד שהקבוע בקדנציה השלישית נמצא ביחידות לחץ (Pa) כדי להבטיח הומוגניות ממדית. משוואה (2) היא "עקומת ביצועי המאוורר" המוצגת באיור 1.
מ"מ בניסוי הנוכחי). המשוואה (2) היא בצורה המבטאת שהקבועים בקדנציה הראשונה והשנייה הם חסרי ממדים, בעוד שהקבוע בקדנציה השלישית נמצא ביחידות לחץ (Pa) כדי להבטיח הומוגניות ממדית. משוואה (2) היא "עקומת ביצועי המאוורר" המוצגת באיור 1.
לבסוף, פיזור האנרגיה הוא פרופורציונלי לאנרגיה הקינטית של הזרימה:
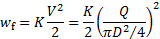 (3)
(3)
שים לב כי באמצעות משוואת ההמשכיות (  ,
, 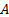 איפה האזור חתך [1, 2]), פיזור האנרגיה יכול להיכתב גם במונחים של קצב הזרימה,
איפה האזור חתך [1, 2]), פיזור האנרגיה יכול להיכתב גם במונחים של קצב הזרימה,  . . איור 1 מציג צורה אחרונה זו של משוואה (3) כ"עקומת מערכת הזרימה". במשוואה (3), מקדם המידתיות
. . איור 1 מציג צורה אחרונה זו של משוואה (3) כ"עקומת מערכת הזרימה". במשוואה (3), מקדם המידתיות  , נקרא מקדם האובדן והוא תוספת של כל ההשפעות הדיסיפטיביות הנגרמות על ידי האלמנטים של מערכת הזרימה כתוצאה מאינטראקציות צמיגות. בעוד שתרומתם של צינורות ותעלות תלויה בחגפוסם, באורךם ובמספר ריינולדס, תרומתם של אביזרי צינורות, כניסות ופריקה, הרחבות, התכווצויות, כיפופים ושסתומים תלויה בגיאומטריות הספציפיות שלהם. עבור הניסוי הנוכחי, מקדם האובדן הכולל הוא שילוב של כניסה, שסתום, ופריקה:
, נקרא מקדם האובדן והוא תוספת של כל ההשפעות הדיסיפטיביות הנגרמות על ידי האלמנטים של מערכת הזרימה כתוצאה מאינטראקציות צמיגות. בעוד שתרומתם של צינורות ותעלות תלויה בחגפוסם, באורךם ובמספר ריינולדס, תרומתם של אביזרי צינורות, כניסות ופריקה, הרחבות, התכווצויות, כיפופים ושסתומים תלויה בגיאומטריות הספציפיות שלהם. עבור הניסוי הנוכחי, מקדם האובדן הכולל הוא שילוב של כניסה, שסתום, ופריקה:
 (4)
(4)
כאשר הערכים של מקדמי ההפסד עבור הכניסה והפריקה הם 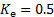
 ובהתאמה (ראה [1, 2] לעיון). מקדם ההפסד עבור השסתום,
ובהתאמה (ראה [1, 2] לעיון). מקדם ההפסד עבור השסתום, 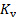 , יידונו בסעיף הבא.
, יידונו בסעיף הבא.
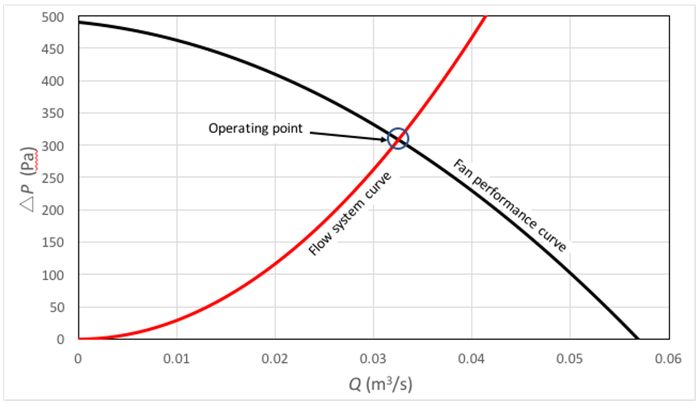
איור 1. דוגמה לעקומת המערכת ועקומת ביצועי המאווררים.  עקומת מערכת;
עקומת מערכת;  עקומת ביצועי המאווררים.: העיגול הכחול מדגיש את ההצטלבות בין שתי העקומות, שהיא נקודת ההפעלה.
עקומת ביצועי המאווררים.: העיגול הכחול מדגיש את ההצטלבות בין שתי העקומות, שהיא נקודת ההפעלה.

איור 2. הגדרה ניסיונית. (א): מתקן זרימה. הזרימה נעה משמאל לימין; היא נכנסת למליאה דרך קטע מיזוג זרימה, ואז זורמת דרך הצינור והשסתום, פולט בתוך המקלט, ולבסוף יוצא מהמערכת דרך המאוורר. (ב): פרטים על מערכת הזרימה וציוד לרכישת נתונים. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

איור 3. מערכת רכישת נתונים. (א) החיבורים של התקני רכישת נתונים אלה עוקבים אחר הדיאגרמה באיור 2(B). (ב) ממשק וירטואלי לרכישת נתונים (כתוב ב- LabView). אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
מאפייני פיזור של שסתום
מאז שסתומים הם בעצם התקנים של גיאומטריה משתנה, מקדם האובדן הספציפי שלהם הוא פונקציה של זווית הסיבוב של הפיר שלהם (  ). עם זה בחשבון,
). עם זה בחשבון, 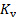 משתנה כמו שסתום נפתח או סגור על פי היחסים הבאים:
משתנה כמו שסתום נפתח או סגור על פי היחסים הבאים:
 (5)
(5)
כאן, השתמשנו שוב במשוואת ההמשכיות כדי לבטא את מקדם ההפסד במונחים של קצב הזרימה. יתר על כן, משוואה (5) מציעה כי אנו יכולים לקבוע את מקדם ההפסד עבור השסתום על ידי ידיעת הערך של קצב הזרימה ואת הלחץ לרדת על פני השסתום כפונקציה של זווית הפתיחה וקצב הזרימה:  . זהו גם הפרש הלחץ בין נקודות 3 ו- 4 באיור 2(B).
. זהו גם הפרש הלחץ בין נקודות 3 ו- 4 באיור 2(B). 
נקודת הפעלה
כפי שמוצג באיור 1, נקודת ההפעלה של מערכת זרימה המונעת על-ידי מכונת זרימה, כמו זו המוצגת בניסוי זה, ניתנת על-ידי נקודת ההצטלבות של העקומה האופיינית של המאוורר ועקומת מערכת הזרימה. נקודה זו יכולה להיות מאופיינת באמצעות משוואת האנרגיה כדלקמן: כפי שניתן לראות באיור 2(A), האוויר נכנס למערכת הזרימה מחדר גדול בתנאים אטמוספריים ויוצא לאותו חדר ללא שינוי משמעותי בגובה. כתוצאה מכך, תנאי הלחץ, המהירות והגובה בפרצון ובשקע של המערכת ( 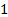
 ותת-קבצים במשוואה (1) בהתאמה) זהים ומבטלים זה את זה. כתוצאה מכך, האנרגיה שנוספה על ידי המאוורר מאוזנת על ידי האנרגיה המתפוגגת על ידי מערכת הזרימה. במילים אחרות, משוואות (2) ו- (3) יוצרות שוויון המביא לקשר הגומלין הבא לאחר פישוט:
ותת-קבצים במשוואה (1) בהתאמה) זהים ומבטלים זה את זה. כתוצאה מכך, האנרגיה שנוספה על ידי המאוורר מאוזנת על ידי האנרגיה המתפוגגת על ידי מערכת הזרימה. במילים אחרות, משוואות (2) ו- (3) יוצרות שוויון המביא לקשר הגומלין הבא לאחר פישוט:
 (6)
(6)
השורש החיובי של משוואה זו מבטא את נקודת ההפעלה:
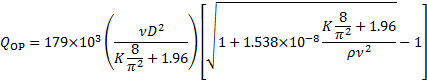 (7)
(7)
כאן, תת-אינדקס "OP" מייצג את "נקודת הפעלה". מקדם האובדן במשוואה (7) הוא תוספת של מקדמי ההפסד של הכניסה, השסתום והפריקה. משוואות (4) ו-(5):
 (8)
(8)
מדידת קצב הזרימה
בדומה לכל ניתוחים קודמים, משווית (1) מוחלת בין המליאה לבין נקודה במורד הזרם של הכניסה החדה (נקודות 2 ו -3 באיור 2(B)) כדי לשחזר את המשוואה הבאה:
 (9)
(9)
כאן השתמשנו בעובדה שאין שינוי בגובה בין נקודות 2 ל-3, והמהירות בתוך המליאה זניחה. בהצגת משוואת ההמשכיות ( 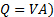 והמשוואה (3), אנו מגיעים ליחסים הבאים עבור קצב הזרימה מבחינת הפרש הלחץ בין המליאה (נקודה 2 באיור 2(B)) לבין הלחץ הסטטי במעלה הזרם של השסתום (נקודה 3 באיור 2(B)):
והמשוואה (3), אנו מגיעים ליחסים הבאים עבור קצב הזרימה מבחינת הפרש הלחץ בין המליאה (נקודה 2 באיור 2(B)) לבין הלחץ הסטטי במעלה הזרם של השסתום (נקודה 3 באיור 2(B)):
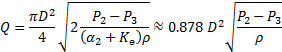 (10)
(10)
0.878 הקבוע מתקבל לאחר החלפת הערכים של מקדם ההפסד ותיקון המהירות ( 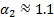
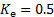 ו, ראה [1, 2] לעיון) וקיבוץ כל הקבועים באחד.
ו, ראה [1, 2] לעיון) וקיבוץ כל הקבועים באחד.
Procedure
1. הגדרת המתקן
- ודא שהמאוורר אינו פועל, כך שאין זרימה במתקן.
- ודא שמערכת רכישת הנתונים (איור 4(A)) פועלת לפי השרטוט באיור 2B.
- חבר את היציאה החיובית של מתמר הלחץ #1 (ראה איור 2B לעיון) לברז הלחץ במעלה הזרם של השסתום (
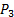 ).
). - השאר את היציאה השלילית של מתמר הלחץ #1 פתוח לתנאי החדר (מקלט:
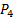 ). לפיכך, הקריאה של מתמר זה יהיה ישירות
). לפיכך, הקריאה של מתמר זה יהיה ישירות  .
. - חבר את היציאה החיובית של מתמר הלחץ #2 (ראו איור 2B לעיון) לברז הלחץ של המליאה (
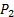 ).
). - חבר את היציאה השלילית של מתמר לחץ #2 (ראה איור 2B לעיון) לברז הלחץ במעלה הזרם של השסתום (
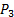 ). לפיכך, הקריאה של מתמר זה תהיה ישירות
). לפיכך, הקריאה של מתמר זה תהיה ישירות  , כנדרש על ידי משוואה (10).
, כנדרש על ידי משוואה (10).
- חבר את היציאה החיובית של מתמר הלחץ #1 (ראה איור 2B לעיון) לברז הלחץ במעלה הזרם של השסתום (
- ודאו שערוץ וירטואלי 0 במערכת רכישת הנתונים(איור 4(B)) מתאים #1 מתמר הלחץ (
 ) לבין ערוץ וירטואלי 1 מתאים #2 מתמר לחץ
) לבין ערוץ וירטואלי 1 מתאים #2 מתמר לחץ  .
. - הגדר את מערכת רכישת הנתונים לדוגמה בקצב של 100 הרץ עבור סך של 500 דוגמאות (כלומר 5s של נתונים).
טבלה 1. פרמטרים בסיסיים למחקר ניסיוני.
|
פרמטר |
ערך |
| קוטר צינור (D) | 50.8 מ"מ (2 אינץ') |
| קבוע כיול #1 מתמר (m_p1) |
|
| קבוע כיול #2 מתמר (m_p2) |
|
| לחץ אטמוספרי מקומי | 100,474.15 אבא |
| טמפרטורה מקומית | 297.15 ק" |
| צפיפות אוויר מקומית | 1.186 ק"ג/מ'3 |

איור 4. מתקן זרימה. (A): מבט על פריקה במליאה לתוך סעיף המקלט לפני התקנת מערכת השסתומים שיש ללמוד. (B): שלושה סוגים שונים של שסתומים בתוך המקלט. משמאל לימין: שסתום שער, שסתום גלובוס, שסתום פרפר. (C): יציאה מיציאות מהמקלט. השסתומים פולטים את הזרימה בתוך המקלט, והמאוורר שואב את הזרימה מהמקלט דרך הצלחת המחוררת בתמונה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
2. מדידות
- תעד את קוטר הצינור המחובר לשסתום וחשב את אזור החתך שלו.
- לקבוע את המספר המרבי של סיבובים מלאים של הידית הנדרשת כדי להעביר את השסתום מהמיקום הסגור לחלוטין למיקום הפתוח לחלוטין. אם מספר זה אינו מספר שלם, אל תכלול את סיבוב השבר האחרון כדי לפשט ניתוח זה. בניסוי הנוכחי, המספר המרבי של סיבובים מלאים הוא 12.
- סגור את השסתום לחלוטין.
- סובב את ידית השסתום עד שהוא פתוח לחלוטין תוך ספירת מספר הפניות המלאות. לפשטות, השתמש במספר שלם בלבד של פניות לניסוי. לדוגמה, זה לוקח בערך 12 סיבובים ו 1/3 של סיבוב כדי לפתוח באופן מלא את השסתום המשמש בניסוי זה. לפיכך, נסובב את הידית של שסתום זה רק 12 סיבובים מלאים ממקומו הסגור לחלוטין ולהגדיר את זה כמיקום הראשוני (
 ).
). - הפעל את מתקן הזרימה.
- השתמש במערכת רכישת הנתונים כדי לתעד את הקריאות של

 ו.
ו. - הזן בטבלה 2 את הערכים הממוצעים של

 מערכת רכישת הנתונים והושגו באמצעות מערכת רכישת הנתונים.
מערכת רכישת הנתונים והושגו באמצעות מערכת רכישת הנתונים. - סגור את השסתום ב-1.5 סיבובים.
- חזור על שלבים 2.6 עד 2.8 עד שלטבלה 2 תהיה מאוכלסת במלואה.
- כבה את מתקן הזרימה.
3. ניתוח נתונים
- לקבוע את מקדם האובדן של השסתום עבור כל מיקום זוויתי באמצעות משוואה (5). הזן ערכים אלה בטבלה 2.
- לקבוע את קצב הזרימה עבור כל מיקום זוויתי של השסתום באמצעות משוואה (10). הזן ערכים אלה בטבלה 2.
- קבע את נקודת ההפעלה באמצעות משוואה (7). הזן ערכים אלה בטבלה 2.
- חישוב ההפרש היחסי בין קצב הזרימה הנמדד לנקודת ההפעלה
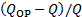
- השתמש במשוואה (3) כדי ליצור התוויה של עקומות המערכת עבור כל הערכים של
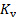 . שקול את מקדם האובדן הכולל כ
. שקול את מקדם האובדן הכולל כ  .
. - הוסף את העקומה האופיינית של המאוורר לאותה חלקה באמצעות משוואה (2).
טבלה 2. תוצאות מייצגות. מדידות של הבדלי לחץ ואומדנים של קצב זרימה ומקדם אובדן.
| [P_a P_pl] (אבא) | [P_r P_a] (אבא) | Q (מ'3/s) | K | Q_OP (m3/s) | ε (%) |
| 246.75 | 54.00 | 0.0327 | 0.450 | 0.0316 | -3.16 |
| 208.62 | 114.22 | 0.0301 | 0.976 | 0.0293 | -2.51 |
| 156.19 | 204.80 | 0.0260 | 2.198 | 0.0254 | -2.30 |
| 109.30 | 281.69 | 0.0218 | 4.224 | 0.0214 | -1.53 |
| 71.82 | 348.38 | 0.0176 | 7.863 | 0.0174 | -1.26 |
| 38.72 | 408.60 | 0.0129 | 16.989 | 0.0128 | -0.90 |
| 15.00 | 452.39 | 0.0081 | 48.359 | 0.0080 | -0.32 |
| 2.51 | 482.50 | 0.0033 | 307.799 | 0.0033 | -0.18 |
Results
איור 5 מציג את התוצאות עבור המדידות הנוכחיות. כאן, הקו המוצק השחור נוצר עם משוואה (2), וכל קו אדום עם משוואה (3) לערכים שונים של מקדם האובדן של השסתום. מהאיור, ניכר כי עקומת המערכת מגדילה את השיפוע שלה עם סגירת השסתום. במילים אחרות, ניסוי זה מדגים כי העיקרון מאחורי הפעולה של שסתום הוא להגביר את פיזור האנרגיה כדי להגביל את הזרימה. מצד שני, ממשוואה (5), ניתן להסיק כי הערך של 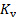 הופך אינסוף כאשר השסתום סגור לחלוטין. מבחינה רעיונית, מצב זה אומר כי כל האנרגיה מתפוגגת, ומכאן לחלוטין לעכב את הזרימה דרך השסתום.
הופך אינסוף כאשר השסתום סגור לחלוטין. מבחינה רעיונית, מצב זה אומר כי כל האנרגיה מתפוגגת, ומכאן לחלוטין לעכב את הזרימה דרך השסתום.
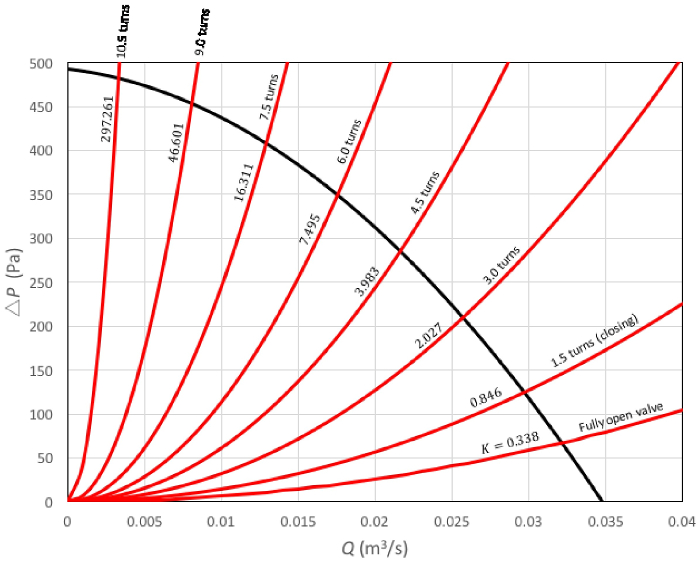
איור 5. תוצאות מייצגות.  עקומות מערכת.: כל עקומה במשפחה זו היא תוצאה של רמה שונה של פתיחת שסתום. השיפוע של העקומות גדל כמו השסתום סגור. לכל עקומה יש את מקדם ההפסדים של הכתבים שלה לעיון;
עקומות מערכת.: כל עקומה במשפחה זו היא תוצאה של רמה שונה של פתיחת שסתום. השיפוע של העקומות גדל כמו השסתום סגור. לכל עקומה יש את מקדם ההפסדים של הכתבים שלה לעיון;  עקומת ביצועי המאווררים.: אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
עקומת ביצועי המאווררים.: אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
כפי שמוצג בטבלה 2, השגיאה בין קצב הזרימה המשוער בנקודת ההפעלה (7)) לבין קצב הזרימה הנמדד (10)) נשארת מתחת ל- 3.2% עבור טווח קצבי הזרימה הנחקרים. למרות שזו תוצאה משביעת רצון בהתחשב בשגיאת האחוזים הקטנה, קצב הזרימה המשוער בנקודת ההפעלה תמיד מוערך, ועוקב אחר נטייה פוחתת כאשר השסתום נסגר בהדרגה. נטייה זו מציעה תובנה מסוימת על אופן הפעולה של מערכת הזרימה, במיוחד משום שהערך של גורם התיקון לאי-אחידות במהירות  עולה מעט עם מספר ריינולדס. לכן אין זה מפתיע כי השגיאה עולה עם קצב הזרימה.
עולה מעט עם מספר ריינולדס. לכן אין זה מפתיע כי השגיאה עולה עם קצב הזרימה.
Application and Summary
ניסוי זה בחן את היישום של משוואת האנרגיה כדי לאפיין את הפעולה של שסתום על זרימת צינור. זה נצפתה כי שסתום גורמת התנגדות זרימה על ידי הגדלת פיזור אנרגיה. בהתחשב בכך ירידה בלחץ לאורך מערכת הזרימה היא פרופורציונלית ישירות לריבוע של קצב הזרימה, ההשפעה של פיזור אנרגיה נתפסת על ידי גודל מקדם המידתיות. מקדם זה הוא תוספת של מקדמי האובדן של כל האלמנטים במערכת הזרימה, כולל השסתום. מקדם ההפסד של השסתום גדל באופן מונוטוני כמו השסתום סגור בהדרגה. ואפקט זה מגדיל את השיפוע של עקומת המערכת כתוצאה מכך, ומגיע לערך של אינסוף כאשר השסתום סגור לחלוטין.
ההתנהגות המתוארת לעיל הייתה מנוגדת לעקומת הביצועים של המאוורר הצנטריפוגלי המניע את הזרימה. על ידי השוואת קצב הזרימה הנמדד ישירות עם קצב הזרימה המוערך על ידי ההצטלבות של עקומת המערכת ועקומת הביצועים של המאוורר, הוכח כי נקודת הצטלבות זו מגדירה את תנאי ההפעלה של קצב הזרימה וביקוש ללחץ.
ניסוי זה שימש את המטרה של הדגמת העקרונות של שימור אנרגיה כדי לאפיין כמה יישומים הנדסיים שונים: פעולת שסתום, מדידת קצב זרימה, ותנאי הפעלה של מערכת זרימה. שימור אנרגיה יכול לשמש בעצם כדי לאפיין כל מערכת זרימה, אלה הן שתי דוגמאות נוספות של יישומים של משוואת האנרגיה:
האנרגיה הקינטית הנישאת על ידי הרוח יכולה להיות נקצרים על ידי טורבינות רוח כדי לייצר חשמל. על ידי השוואת במעלה הזרם לתנאי זרימה במורד הזרם, ניתן להשתמש במשוואת האנרגיה כדי להעריך כמה אנרגיה הוסרה מהרוח. גודל האנרגיה התאושש יינתן על ידי עבודת פיר,  , במשוואה (1).
, במשוואה (1).
שינוי באנרגיה הפוטנציאלית הכבידתית יכול לשמש להערכת קצב זרימת המים מעל שפך. זה נעשה בשילוב עם משוואת שימור ההמונים על ידי מדידת המעמקים במעלה הזרם ובמורד הזרם של הזרימה. עבור זרימה סוערת, המשוואה הבאה תהיה קירוב טוב לקצב הזרימה מעל הדליפה:
 (11)
(11)
כאן,  הוא רוחב הערוץ
הוא רוחב הערוץ  והם
והם  המעמקים במעלה ובמורד הזרם בהתאמה.
המעמקים במעלה ובמורד הזרם בהתאמה.
Tags
Skip to...
Videos from this collection:

Now Playing
שימור הגישה האנרגטית לניתוח מערכות
Mechanical Engineering
7.4K Views

ציפה וגרירה על גופים שקועים
Mechanical Engineering
30.2K Views

יציבות של כלי שיט צפים
Mechanical Engineering
23.3K Views

הנעה ודחף
Mechanical Engineering
22.1K Views

רשתות צנרת והפסדי לחץ
Mechanical Engineering
58.9K Views

מרווה ומרתיח
Mechanical Engineering
8.2K Views

קפיצות הידראוליות
Mechanical Engineering
41.3K Views

ניתוח מחליף חום
Mechanical Engineering
28.3K Views

מבוא לקירור
Mechanical Engineering
25.0K Views

שושנת ים של חוט חם
Mechanical Engineering
15.9K Views

מדידת זרמים סוערים
Mechanical Engineering
13.6K Views

הדמיה של זרימה בעבר גוף בלוף
Mechanical Engineering
12.3K Views

ג'ט פוגע בלוח נוטה
Mechanical Engineering
10.8K Views

מדידות של שימור המוני וקצב זרימה
Mechanical Engineering
23.0K Views

קביעת כוחות מניעה על לוח שטוח בשיטת אמצעי האחסון של הפקד
Mechanical Engineering
26.0K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved