Conservazione di massa e misure di portata

Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Dipartimento di Ingegneria Meccanica, Michigan State University, East Lansing, MI

Lo scopo di questo esperimento è dimostrare la calibrazione di un passaggio di flusso come misuratore di portata utilizzando una formulazione di volume di controllo (CV) [1, 2]. L'analisi CV si concentra sull'effetto macroscopico del flusso sui sistemi di ingegneria, piuttosto che sulla descrizione dettagliata che potrebbe essere ottenuta con un'analisi differenziale dettagliata. Queste due tecniche dovrebbero essere considerate approcci complementari, in quanto l'analisi del CV fornirà all'ingegnere una base iniziale su quale percorso perseguire durante la progettazione di un sistema di flusso. In generale, un'analisi CV darà all'ingegnere un'idea dello scambio di massa dominante in un sistema e dovrebbe idealmente essere il passo iniziale da compiere prima di perseguire qualsiasi progettazione o analisi dettagliata tramite formulazione differenziale.

Il principio principale alla base della formulazione CV per la conservazione della massa è quello di sostituire i dettagli di un sistema di flusso con un volume semplificato racchiuso in quella che è nota come superficie di controllo (CS). Questo concetto è immaginario e può essere definito liberamente per semplificare abilmente l'analisi. Ad esempio, il CS dovrebbe "tagliare" le porte di ingresso e di uscita in una direzione perpendicolare alla velocità dominante. Quindi, l'analisi consisterebbe nel trovare l'equilibrio tra il flusso di massa netto attraverso il CS e il tasso di variazione della massa all'interno del CV. Questa tecnica sarà dimostrata con la calibrazione di una contrazione liscia come flussometro.

Un volume di controllo (CV) è definito da una superficie chiusa immaginaria, soprannominata superficie di controllo (CS), definita arbitrariamente per studiare l'equilibrio di massa in un sistema. La Figura 1A mostra un esempio di volume di controllo contenente una regione di flusso che attraversa un passaggio di flusso. I dettagli del flusso nel passaggio sono irrilevanti poiché siamo semplicemente interessati a ottenere misure dell'afflusso di massa, del deflusso e della sua velocità di cambiamento all'interno del passaggio del flusso. Tutti questi effetti possono essere riassunti nell'equazione per la conservazione della massa in forma integrale [1, 2]:

(1)

Il primo termine sul lato destro dell'equazione (1) rappresenta il tasso di variazione della massa all'interno del volume di controllo, mentre il secondo termine rappresenta il flusso netto di massa attraverso la superficie di controllo. La differenza vettoriale 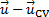è la velocità relativa tra il CV e il flusso, e il vettore è l'unità verso l'esterno normale al differenziale di area. Il prodotto punto tra la velocità relativa e rappresenta la componente di velocità che attraversa il CS, e d'ora in poi contribuisce allo scambio di massa. Il segno di questo prodotto punto è negativo dove il flusso di massa è diretto nel CV e positivo dove è diretto lontano dal CV.

Figura 1. Scematica della configurazione di base. (A) Aspirazione regolare per un ventilatore centrifugo. Il volume di controllo è definito come il profilo interno del passaggio. Le pareti solide sono escluse dal volume di controllo, ma le loro condizioni al contorno sono mantenute nella superficie di controllo (cioè nessuna penetrazione e nessuna scivolata). La porta 1 è definita come il lato d'ingresso del passaggio, mentre la porta 2 è definita come il piano della sezione trasversale che coincide con la punta del tubo di Pitot. Il flusso va da sinistra a destra. (B) Sistema pitot-statico e schema cdel sistema di acquisizione dati. Fare clic qui per visualizzare una versione più ampia di questa figura.

Per la presente dimostrazione, abbiamo le configurazioni mostrate in Figura 1A, dove un CV fisso segue il contorno di una contrazione liscia all'ingresso di un ventilatore centrifugo. Il flusso attraverso questo CV è costante, quindi la velocità di variazione della massa all'interno del volume di controllo è zero. Quindi, il primo termine sul lato destro dell'equazione (1) svanisce. Inoltre, il CV è attaccato alla contrazione, che è fissata nello spazio e non ha velocità, facendo 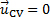. Pertanto, il flusso netto di massa attraverso questo CV è zero e l'equazione (1) semplifica a:

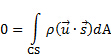(2)

Considerando la configurazione nella Figura 1A, la massa fluisce nel CV attraverso la porta 1 e lascia il CV attraverso la porta 2. Di conseguenza, l'integrale di superficie sul lato destro dell'equazione (2) può essere diviso in due integrali indipendenti, uno per ogni porta. Il segno del prodotto punto è negativo nella porta 1 perché il flusso va verso il CV e positivo nella porta 2 perché il flusso si allontana dal CV. Senza supporre che la velocità sia distribuita in modo omogeneo in entrambe le porte, facciamo 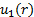e 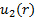i rispettivi profili di velocità tenendo conto che entrambi sono ciò che rimane dopo aver preso il prodotto punto. Cioè, la grandezza della componente di velocità parallela al vettore di area, . Infine, i cambiamenti di pressione lungo la contrazione non sono abbastanza significativi da indurre cambiamenti osservabili nella densità. D'ora in poi, possiamo considerare la densità come costante. In queste circostanze, l'equazione (2) semplificherebbe per:

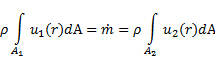(3)

Si noti che, poiché la massa è conservata, il flusso di massa, , è lo stesso attraverso entrambe le porte. Data la struttura di queste relazioni, ogni integrale nell'equazione (3) esprime la portata volumetrica, , attraverso la sua porta corrispondente, e questo fatto aiuta a definire la velocità media, 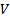, per una data porta:

(4)

In condizioni inviscide, la velocità alla porta 2 potrebbe essere espressa in termini di condizioni al di fuori dell'aspirazione usando l'equazione di Bernoulli lungo la razionalizzazione centrale (vedi Figura 1A per riferimento):

(5)

Qui, l'effetto dell'altezza svanisce sulla linea centrale perché è orizzontale, ed è trascurabile nelle altre linee di flusso perché il fluido è l'aria, che ha un peso specifico molto piccolo. Inoltre, il punto iniziale sulla streamline centrale è sufficientemente lontano dall'ingresso che la sua velocità è zero. Dato che l'equazione (5) è per il caso inviscido idealizzato, questo valore di velocità sarà lo stesso in tutta la porta 2. In realtà, la crescita dello strato limite influisce sul profilo di velocità e lo rende non omogeneo. Per tenere conto di questo effetto, la stima ideale viene confrontata con misurazioni sperimentali tramite il "Coefficiente di scarica". Questo coefficiente è definito come il rapporto tra la velocità media misurata e la velocità inviscida per una data sezione trasversale del flusso:

(6)

Il coefficiente di scarica, , dipende dalla geometria e dal numero di Reynolds. Una volta determinato, potrebbe essere utilizzato in combinazione con le equazioni (4) e (5) per determinare la portata attraverso la porta 2 in base alla sua area di sezione trasversale e un differenziale di pressione facile da misurare:

(7)

Quando si mettono insieme le equazioni (4), (5) e (6) e si considera che la porta 2 è circolare, si ottiene la seguente relazione per:

(8)

Dall'equazione (8) risulta chiaramente che la conoscenza del profilo di velocità è necessaria per ottenere il coefficiente di scarica. A tal fine, utilizzeremo la velocimetria di Pitot - sonde statiche. Come mostrato in Figura 1B, il tubo di Pitot porta il flusso ad un arresto rilevando la pressione totale, 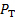, che è l'aggiunta delle pressioni statiche e dinamiche in un dato punto. D'altra parte, la sonda statica a parete rileva la sola pressione statica. Dall'equazione di Bernoulli applicata in una data posizione radiale, la pressione totale è solo la costante di Bernoulli. Alla porta 2, questo principio può essere espresso dalla seguente relazione in una posizione radiale arbitraria:

(9)

Qui, stiamo trascurando l'effetto della posizione verticale perché il nostro passaggio di flusso è orizzontale. In sintesi, si ottiene la seguente relazione per la grandezza della velocità in una data posizione 'r' all'interno del tubo:

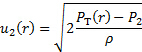(10)

La differenza di pressione viene misurata direttamente dal trasduttore di pressione raffigurato nella Figura 1B e il profilo di velocità si ottiene attraversando il tubo di Pitot lungo la coordinata radiale del tubo. Si noti che queste misurazioni della velocità vengono eseguite in posizioni discrete, quindi questi punti dati dovrebbero essere usati per risolvere l'integrale nell'equazione (8) numericamente usando la regola trapezoidale o simpson [1]. Una volta ottenuto il valore di questo integrale, dovrebbe essere inserito nell'equazione (8) insieme al valore misurato di , la densità e il raggio del condotto, per ottenere il valore di per quella particolare condizione di flusso. Dopo aver ripetuto questo esperimento per diverse condizioni di flusso, otterremo un grafico a dispersione che potrebbe essere utilizzato per determinare una relazione tra e . Questa relazione può quindi essere sostituita nell'equazione (7) per determinare completamente la portata, , in funzione di solo .

1. Impostazione della struttura

1. Assicurati che non ci sia flusso nella struttura.
2. Verificare che il sistema di acquisizione dati segua lo schema nella Figura 1B.
3. Collegare la porta positiva del trasduttore di pressione #1 (vedere figura 1B per riferimento) al tubo di Pitot che attraversa ( ).
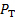4. Collegare la porta negativa di questo stesso trasduttore di pressione alla sonda statica del passaggio di aspirazione ( ). Quindi, la lettura di questo trasduttore di pressione sarà direttamente ( ).
5. Registrare il fattore di conversione di questo trasduttore da Volt a Pascal ( 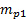). Immettere questo valore nella tabella 1.
6. Collegare la porta positiva del trasduttore di pressione #2 (vedere la Figura 1B per riferimento) alla sonda statica del passaggio di aspirazione ( ) utilizzando un tee.
7. Lasciare la porta negativa del trasduttore di pressione #2 aperta all'atmosfera ( 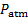). Quindi, la lettura di questo trasduttore sarà direttamente ( ).
8. Registrare il fattore di conversione di questo trasduttore da Volt a Pascal ( ). Immettere questo valore nella tabella 1.
9. Impostare il sistema di acquisizione dati per campionare ad una velocità di 100 Hz per un totale di 500 campioni (cioè 5s di dati).
10. Assicurarsi che il canale 1 nel sistema di acquisizione dati corrisponda al trasduttore di pressione #1 ( ).
11. Inserire il fattore di conversione 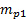nel sistema di acquisizione dati per assicurarsi che la misurazione della pressione ( ) venga convertita direttamente in Pascal.
12. Impostare la sonda Pitot alla fine del suo viaggio, dove tocca la parete del tubo. Poiché la sonda ha un diametro di 2 mm, il primo punto di velocità si trova a una coordinata radiale a 1 mm di distanza dalla parete. Cioè, in una posizione radiale di mm (qui, mm).

Figura 2. Impostazione sperimentale. (A): Passaggio del flusso in fase di studio. (B): sistema di attraversamento manuale per il tubo di Pitot. Fare clic qui per visualizzare una versione più grande di questa figura.

Tabella 1. Parametri di base per lo studio sperimentale. Valore del misuratore di parità

Parametro	Valore
Raggio di passaggio del flusso (Ro)	82,25 mm
Costante di calibrazione #1 del trasduttore (m_p1)	136,015944 Pa/V
Costante di calibrazione #2 del trasduttore (m_p2)	141,241584 N/V
Pressione atmosferica locale	100.474,15 Pa
Temperatura locale	297,15 K
P_atm-P_2	311,01 Pa

2. Misurazioni

1. Accendere la struttura di flusso.
2. Registrare la lettura del trasduttore di pressione #2 in Volt dal multimetro digitale.
3. Immettere questo valore nella Tabella 1 come e convertire la lettura da Volt a Pascal utilizzando il fattore .
4. Utilizzare il sistema di acquisizione dati per registrare la lettura di ( ).
5. Immettere il valore di nella tabella 2.
6. Utilizzare la manopola di attraversamento per modificare la posizione radiale del tubo di Pitot in base al valore suggerito nella Tabella 2.
7. Ripetere i passaggi 2.4 e 2.6 fino a quando la tabella 2 non è completamente popolata.
8. Modificare la portata variando la scarica del sistema.
9. Ripetere i passaggi da 2,4 a 2,8 per almeno dieci diverse portate.
10. Spegnere la struttura di flusso.

Figura 5. Impostazione sperimentale. Piastre forate per limitare il flusso allo scarico del sistema di flusso. Fare clic qui per visualizzare una versione più grande di questa figura.

Tabella 2. Risultati rappresentativi. Misurazioni della velocità. r (mm) P_T - P₂ (Pa) u (r) (m/s

r (mm)	PT - P2 (Pa)	u(r) (m/s)
2.25	300.35	22.34
12.25	302.84	22.43
22.25	305.82	22.54
32.25	302.34	22.41
42.25	294.88	22.13
52.25	295.37	22.15
62.25	292.88	22.06
68.25	293.63	22.09
72.25	294.13	22.10
75.25	299.60	22.31
77.25	293.13	22.07
79.25	284.67	21.75
80.25	256.31	20.63
81.25	198.33	18.15

3. Analisi dei dati.

1. Determinare il profilo di velocità utilizzando i valori di differenza di pressione, P_T - P_2, dalla Tabella 2. Immettere i risultati nella Tabella 2.
2. Tracciare sia i valori di pressione che di velocità della Tabella 2 usando il raggio, , come le ascisse (Figura 3).
3. Calcolare l'integrale nell'equazione (8) in base ai valori di velocità e raggio della Tabella 2.
4. Calcolare il coefficiente di scarica per ogni portata utilizzando l'equazione (8).
5. Traccia il coefficiente di scarico usando 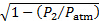come ascisse.
6. Adatta una funzione al coefficiente di scarica, una legge di potenza è una buona scelta.

Figura 3. Risultati rappresentativi. (A): Esempio di misura della pressione statica lungo la coordinata radiale del passaggio del flusso. (B): Distribuzione della velocità determinata dalle misurazioni della pressione statica. Fare clic qui per visualizzare una versione più grande di questa figura.

Per una data restrizione del flusso allo scarico del ventilatore, la Figura 3A mostra le misurazioni della pressione dinamica ( ) in diverse posizioni radiali all'interno del tubo dopo l'attraversamento con il tubo di Pitot. Questi valori sono stati utilizzati per determinare la velocità locale in quelle posizioni radiali e i risultati sono mostrati nella Figura 3B. Dopo aver usato la regola trapezoidale su questi dati per risolvere l'equazione (4) per la velocità media, abbiamo ottenuto un valore di m/s. D'altra parte, il valore di dalla Tabella 1 è stato utilizzato per determinare la velocità ideale dall'equazione (5): m/s. Quindi, il coefficiente di scarica per questa condizione di flusso è: 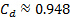. Questo valore è mostrato nella Figura 4 come un triangolo rosso.

Dopo aver ripetuto questo esperimento altre ventinove volte, abbiamo ottenuto il grafico a dispersione mostrato nella Figura 4. Questi dati possono essere ben rappresentati da una legge di potenza 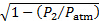di:

(11)

La ragione di questa scelta di argomentazione è assicurarsi che la costante principale rimanga adimensionale, e quindi questa correlazione sarebbe ancora valida indipendentemente dal sistema di unità utilizzate per la pressione. Questa funzione può essere sostituita nell'equazione (7) per ottenere la portata in funzione di :

(12)

Qui, tutte le costanti delle equazioni (7) e (11) sono state raggruppate in un'unica costante adimensionale: 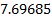. Di conseguenza, l'equazione (12) è valida per qualsiasi sistema di unità purché alle variabili siano assegnate in modo coerente le unità corrispondenti. Per comodità, la densità dell'equazione (7) è stata espressa in termini di pressione atmosferica e temperatura assoluta usando la legge del gas ideale. L'equazione (12) è valida per diverse condizioni atmosferiche in quanto tiene conto delle variazioni della pressione e della temperatura locali (T e P_atm). Inoltre, finché la somiglianza geometrica è conservata, questa equazione sarebbe valida per passaggi di diverse dimensioni come spiegato dal raggio R.

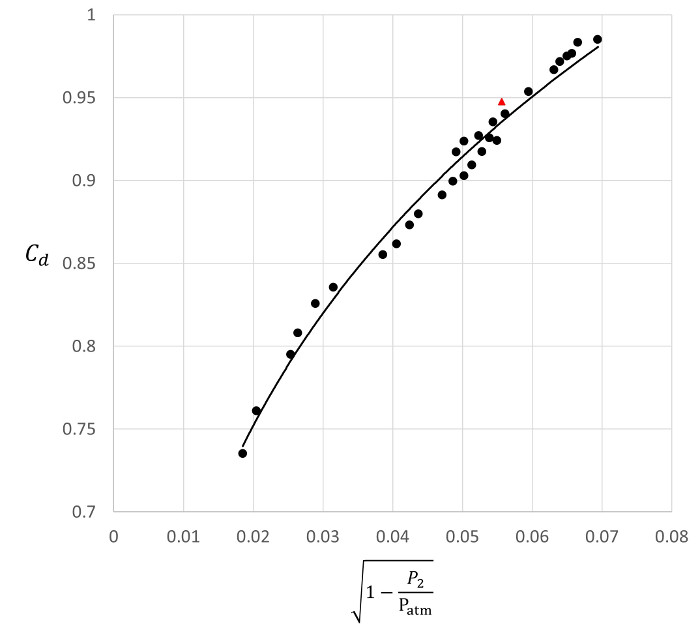
Figura 4. Risultati rappresentativi. : Coefficienti di scarico determinati a diverse portate. : Coefficiente di scarica determinato con le misurazioni della velocità qui dimostrate. - : Legge di potenza adattata ai dati sperimentali.

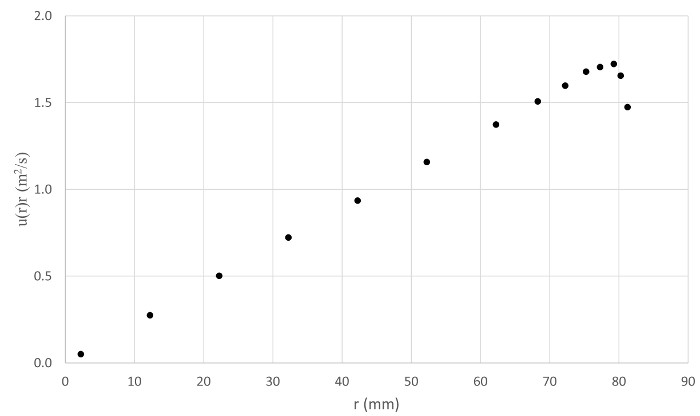
Figura 6. Risultati rappresentativi. Grafico del prodotto tra velocità e raggio.

Tabella 3. Risultati rappresentativi. Coefficiente di scarico.

√(1-P2/Patm)	Cd
0.019	0.735
0.020	0.761
0.025	0.795
0.026	0.808
0.029	0.826
0.032	0.835
0.039	0.855
0.041	0.862
0.042	0.873
0.044	0.880
0.047	0.891
0.049	0.899
0.049	0.917
0.050	0.924
0.050	0.903
0.051	0.909
0.052	0.927
0.053	0.917
0.054	0.926
0.054	0.935
0.055	0.924
0.056	0.940
0.060	0.953
0.063	0.967
0.064	0.972
0.065	0.975
0.066	0.977
0.067	0.983
0.069	0.985

Abbiamo dimostrato l'applicazione dell'analisi del volume di controllo della conservazione della massa per calibrare un passaggio di flusso come misuratore di portata. A tal fine, abbiamo dimostrato l'uso di un sistema Pitot-statico per determinare la portata attraverso il passaggio del flusso utilizzando l'integrazione sul profilo di velocità. Quindi, il concetto di coefficiente di scarico è stato incorporato per tenere conto dell'effetto della crescita dello strato limite vicino alle pareti del passaggio del flusso. Sulla base di una serie di misurazioni della velocità per diverse portate, abbiamo sviluppato una regressione che esprime il coefficiente di scarica in funzione del rapporto tra la pressione statica al passaggio del flusso e la pressione atmosferica locale, . Infine, questa regressione è stata incorporata in un'equazione per la portata attraverso il passaggio in funzione di . Questa equazione è stata sviluppata per mantenere la sua validità in caso di cambiamenti nelle condizioni atmosferiche locali, nelle dimensioni del passaggio e nel sistema unitario.

L'analisi del volume di controllo per la conservazione della massa offre molte alternative per calibrare i passaggi di flusso come misuratori di portata. Ad esempio, piastre perforate, ugelli e tubi venturi vengono utilizzati in flussi confinati per determinare la portata in base alle variazioni di pressione tra due diverse sezioni del passaggio. E simile al nostro esempio, questi dispositivi devono essere caratterizzati con un coefficiente di scarica che corregge gli effetti dello strato limite.

Nel flusso attraverso canali aperti, l'analisi del volume di controllo per la conservazione della massa può anche essere utilizzata per valutare la portata confrontando la profondità del flusso prima e dopo le restrizioni di flusso come sfioratori, cancelli parzialmente aperti o riduzioni della sezione trasversale. Il significato principale di queste applicazioni è che le strutture idrauliche per la distribuzione, il controllo e il trattamento dell'acqua sono di dimensioni molto grandi che precluderebbero l'uso di altri dispositivi di flusso.