Getto che incide su una piastra inclinata
Panoramica
Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Dipartimento di Ingegneria Meccanica, Michigan State University, East Lansing, MI
L'obiettivo di questo esperimento è dimostrare come un flusso di fluido eserciti forze sulle strutture mediante la conversione della pressione dinamica in pressione statica. A tal fine, faremo impattare un jet aereo su una piastra piana e misureremo la distribuzione della pressione risultante lungo la piastra. La forza risultante sarà stimata integrando il prodotto tra la distribuzione della pressione e i differenziali di area opportunamente definiti lungo la superficie della piastra. Questo esperimento verrà ripetuto per due angoli di inclinazione della piastra rispetto alla direzione del getto e due portate. Ogni configurazione produce una diversa distribuzione della pressione lungo la piastra, che è il risultato di diversi livelli di conversione della pressione dinamica in pressione statica sulla superficie della piastra.
Per questo esperimento, la pressione verrà misurata con un trasduttore di pressione a membrana collegato a una valvola di scansione. La piastra stessa ha piccole perforazioni chiamate rubinetti a pressione che si collegano alla valvola di scansione attraverso tubi. La valvola di scansione invia la pressione da questi rubinetti al trasduttore di pressione uno alla volta. La pressione induce una deflessione meccanica sul diaframma che il trasduttore di pressione converte in tensione. Questa tensione è proporzionale alla differenza di pressione tra i due lati del diaframma.
Principi
In flussi costanti incomprimibili con cambiamenti trascurabili nel potenziale gravitazionale, l'equazione di Bernoulli potrebbe essere interpretata come l'aggiunta di due forme di energia: energia cinetica ed energia potenziale di pressione. In un processo inviscido, queste forme di energia sono libere di trasformarsi l'una nell'altra lungo linee di flusso mantenendo costante la quantità totale iniziale di energia. Questa energia totale è chiamata costante di Bernoulli. Per comodità, l'equazione di Bernoulli può essere espressa in dimensioni di pressione usando il principio dell'omogeneità dimensionale [3]. Sotto questa trasformazione dimensionale, il termine associato all'energia cinetica è soprannominato "pressione dinamica", il termine associato all'energia potenziale di pressione è chiamato "pressione statica" e la costante di Bernoulli è chiamata "pressione di ristagno". Quest'ultima può essere interpretata come la pressione massima che il flusso raggiungerebbe se portato ad un arresto trasformando tutta la sua pressione dinamica in pressione statica. Questi principi possono essere meglio descritti dalla seguente forma dell'equazione di Bernoulli:
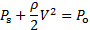 (1)
(1)
Dove 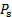 è la pressione statica,
è la pressione statica,  è la pressione dinamica e è la
è la pressione dinamica e è la  pressione di ristagno. La Figura 1(A) mostra uno schema dell'esperimento corrente. Come mostrato, un getto d'aria esce da un plenum ad alta pressione attraverso una fessura di larghezza W e si estende su L in uno spazio chiuso a una pressione inferiore denominata ricevitore. Il ricevitore è una piccola stanza che funge da sezione di test per l'esperimento. Ospita le apparecchiature di acquisizione dati e gli sperimentatori. Dopo aver fluito per una certa distanza, il getto impatta su una piastra piana all'interno del ricevitore che fa un angolo con l'asse del getto. Il getto nella figura 1 (A) è delineato da tre linee di flusso. La linea di flusso intermedia divide il getto in due regioni, una che viene deviata verso l'alto e una che viene deviata verso il basso. Poiché la linea di demarcazione non viene deviata, si ferma proprio al muro in quello che è noto come il punto di ristagno. A quel punto, tutta la pressione dinamica viene convertita in pressione statica e la pressione raggiunge il suo livello massimo,
pressione di ristagno. La Figura 1(A) mostra uno schema dell'esperimento corrente. Come mostrato, un getto d'aria esce da un plenum ad alta pressione attraverso una fessura di larghezza W e si estende su L in uno spazio chiuso a una pressione inferiore denominata ricevitore. Il ricevitore è una piccola stanza che funge da sezione di test per l'esperimento. Ospita le apparecchiature di acquisizione dati e gli sperimentatori. Dopo aver fluito per una certa distanza, il getto impatta su una piastra piana all'interno del ricevitore che fa un angolo con l'asse del getto. Il getto nella figura 1 (A) è delineato da tre linee di flusso. La linea di flusso intermedia divide il getto in due regioni, una che viene deviata verso l'alto e una che viene deviata verso il basso. Poiché la linea di demarcazione non viene deviata, si ferma proprio al muro in quello che è noto come il punto di ristagno. A quel punto, tutta la pressione dinamica viene convertita in pressione statica e la pressione raggiunge il suo livello massimo,  . Il livello di pressione diminuisce lontano dal punto di ristagno perché la pressione progressivamente meno dinamica viene convertita in pressione statica.
. Il livello di pressione diminuisce lontano dal punto di ristagno perché la pressione progressivamente meno dinamica viene convertita in pressione statica.
A seconda dell'angolo di impingement 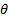 (in figura 1), la streamline di stagnazione segue un percorso diverso. Quando
(in figura 1), la streamline di stagnazione segue un percorso diverso. Quando  , la linea centrale del getto è anche la linea di ristagno streamline. Man mano
, la linea centrale del getto è anche la linea di ristagno streamline. Man mano 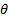 che diminuisce, la linea di ristagno si allontana dalla linea di mezzeria del getto, verso traiettorie che iniziano più vicino al bordo esterno del getto. Poiché 90o è anche la traiettoria della velocità massima, ergo pressione dinamica massima, il suo punto di ristagno risultante raggiungerà il valore massimo di pressione rispetto ad altre traiettorie a valori più piccoli di
che diminuisce, la linea di ristagno si allontana dalla linea di mezzeria del getto, verso traiettorie che iniziano più vicino al bordo esterno del getto. Poiché 90o è anche la traiettoria della velocità massima, ergo pressione dinamica massima, il suo punto di ristagno risultante raggiungerà il valore massimo di pressione rispetto ad altre traiettorie a valori più piccoli di 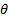 . In sintesi, l'effetto dell'angolo di impingement sul profilo di pressione è quello di ridurre il suo valore massimo e spostare il suo picco verso le regioni della piastra più vicine all'uscita del getto.
. In sintesi, l'effetto dell'angolo di impingement sul profilo di pressione è quello di ridurre il suo valore massimo e spostare il suo picco verso le regioni della piastra più vicine all'uscita del getto.
La linea tratteggiata nella figura 1 (A) rappresenta la distribuzione della pressione netta lungo la superficie della piastra esposta al getto. Si noti dalla figura 1 (B) che la pressione totale sulla piastra, 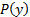 , è l'aggiunta della pressione
, è l'aggiunta della pressione 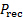 circostante, , più la pressione di impingement o sovrapressione,
circostante, , più la pressione di impingement o sovrapressione, 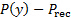 . Poiché la pressione circostante è distribuita in modo omogeneo, si annulla e il carico sulla piastra è strettamente il risultato della sovrapressione. Questa distribuzione della pressione sarà determinata sperimentalmente e utilizzata per stimare il carico netto sulla piastra in base al seguente integrale:
. Poiché la pressione circostante è distribuita in modo omogeneo, si annulla e il carico sulla piastra è strettamente il risultato della sovrapressione. Questa distribuzione della pressione sarà determinata sperimentalmente e utilizzata per stimare il carico netto sulla piastra in base al seguente integrale:
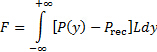 (2)
(2)
Poiché i dati sperimentali sono discreti, questo integrale può essere stimato usando la regola trapezoidale o la regola di Simpson [4].
Inoltre, quando i fluidi vengono scaricati da una regione di pressione più elevata a una regione di pressione inferiore attraverso orifizi o fessure, il getto di emissione tende a convergere inizialmente in una regione chiamata vena contracta (vedi Figura 1 per riferimento) e poi diverge in seguito mentre scorre lontano dalla porta di scarico [5]. La vena contracta è infatti la prima posizione dopo che un getto lascia la sua porta di scarico in cui le linee di flusso diventano parallele. Di conseguenza, questo è il primo posto lungo il getto in cui la pressione statica è uguale alla pressione dell'ambiente circostante [5]. Nel presente esperimento, il plenum è la regione ad alta pressione e il ricevitore è la regione a bassa pressione. Inoltre, la velocità all'interno del plenum è trascurabile e può essere considerata stagnante con un'ottima approssimazione. Quindi, l'equazione (1) potrebbe essere usata per determinare la velocità al contratto della venaa come segue:
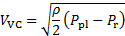 (3)
(3)
Ecco,  la differenza di pressione tra il plenum e il ricevitore. In generale, il rapporto di contrazione tra la larghezza della fessura e la vena contratta è molto approssimativa [5, 6, 7]:
la differenza di pressione tra il plenum e il ricevitore. In generale, il rapporto di contrazione tra la larghezza della fessura e la vena contratta è molto approssimativa [5, 6, 7]:
 (4)
(4)
Quindi, la portata massiva può essere stimata da (3) e (4) come segue:
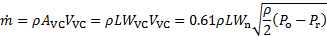 (5)
(5)
Ecco,  la zona della vena contracta.
la zona della vena contracta.

Figura 1. Schema della configurazione di base. Un getto aereo esce dal plenum nel ricevitore attraverso una fessura di larghezza W. Il getto impatta su una piastra inclinata e viene deviato mentre esercita un carico di pressione sulla superficie (linea tratteggiata). Fare clic qui per visualizzare una versione più grande di questa figura.
Procedura
1. Impostazione della struttura
- Assicurati che non ci sia flusso nella struttura.
- Impostare gli strumenti secondo lo schema in figura 2.
- Regolare la piastra all'angolo desiderato
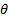 . Registrare questo valore nella tabella 1.
. Registrare questo valore nella tabella 1. - Misurare la larghezza dell'ugello a getto W. Registrare questo valore nella tabella 1.
- Misurare la campata della piastra L. Registrare questo valore nella tabella 1.
- Azzerare il trasduttore di pressione.
- Si noti la costante di calibrazione del trasduttore di pressione, mp (Pa/V). Registrare questo valore nella tabella 1.
- Collegare la porta ad alta pressione del trasduttore (contrassegnata come +) al rubinetto di pressione del plenum (contrassegnato come
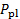 ).
). - Poiché tutte le operazioni avvengono all'interno del ricevitore, lasciare aperta la porta a bassa pressione del trasduttore (contrassegnata come -) per percepire la pressione nel ricevitore (
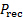 ).
). - Avviare l'impianto di flusso (FLL).
- Utilizzare il multimetro digitale per registrare la tensione
 (V) associata alla differenza di pressione tra il plenum e il ricevitore rilevata dal trasduttore di pressione. Registrare questo valore nella tabella 2.
(V) associata alla differenza di pressione tra il plenum e il ricevitore rilevata dal trasduttore di pressione. Registrare questo valore nella tabella 2. - Utilizzare la costante di calibrazione mp da 1,7 per determinare la differenza di pressione tra il plenum e il ricevitore (
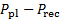 ). Registrare questo valore nella tabella 2.
). Registrare questo valore nella tabella 2.

Figura 2 . Dettagli del sistema di acquisizione dati. Schema per i collegamenti delle apparecchiature. Fare clic qui per visualizzare una versione più grande di questa figura.
Tabella 1 . Parametri di base per lo studio sperimentale.
| Parametro | Valore |
| Larghezza dell'ugello agetto( Wn) | 41,3 mm |
| Span della piastra (L) | 81,3 cm |
| Altezza piastra (H) | 61 centimetri |
| Costante di calibrazione del trasduttore (m_p) | 137,6832 Pa/V |
2. Esecuzione dell'esperimento
- Collegare la porta ad alta pressione del trasduttore (contrassegnata come +) alla porta comune della valvola di scansione. Lasciare aperta la porta a bassa pressione del trasduttore (contrassegnata come -) per percepire la pressione nel ricevitore (
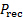 ).
). - Inserire la valvola di scansione per avviare la misurazione dalla prima posizione del rubinetto di pressione.
- Eseguire Il Traverse VI (strumento virtuale LabView).
- Immettere la costante di calibrazione mp nel VI.
- Impostare la frequenza di campionamento su 100 Hz e il totale dei campioni su 500 (ovvero 5 secondi di dati).
- Inserire nel VI la posizione (
 ) del rubinetto di pressione da cui verranno acquisiti i dati di pressione della piastra. Tenere conto del fatto che i rubinetti a pressione sono distanziati di 25,4 mm. Quindi, la posizione sarà
) del rubinetto di pressione da cui verranno acquisiti i dati di pressione della piastra. Tenere conto del fatto che i rubinetti a pressione sono distanziati di 25,4 mm. Quindi, la posizione sarà  mm, dove
mm, dove 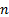 è l'indice del rubinetto che inizia da 0.
è l'indice del rubinetto che inizia da 0. - Registrare i dati. Il VI leggerà la differenza di pressione tra il rubinetto di pressione e il ricevitore (
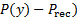 .
. - Portare la valvola di scansione alla posizione successiva del rubinetto.
- Ripetere i passaggi da 2,6 a 2,8 fino a quando tutti i rubinetti di pressione non vengono attraversati.
- Alla fine, il VI fornisce una tabella e un grafico della posizione del rubinetto rispetto alla pressione.
- Ferma il VI.
- Modificare la posizione della piastra di controllo del flusso per chiudere l'area di flusso all'incirca della metà (vedere la Figura 3 per riferimento). Questo modificherà la portata. Utilizzare Equazione (5) per determinare il valore di questa portata.
- Ripetere i passaggi da 2,3 a 2,11 per la nuova posizione della piastra di controllo del flusso.
- Modificate l'angolo della piastra di impingement e impostate la piastra di controllo del flusso nella sua posizione iniziale.
- Ripetere i passaggi da 2,3 a 2,14 per 80o,70o,60o,50oe 45o.

Figura 3 . Impostazione sperimentale. Sezione di prova. A sinistra: piastra di impingement davanti alla fessura. L'aria ad alta pressione viene scaricata dal plenum nel ricevitore attraverso questa fessura. Centro: i rubinetti di pressione collegati alla piastra di impingement sono distribuiti nella valvola di scansione per campionare uno alla volta. A destra: piastra di impingement davanti alla scarica del ricevitore. Lo scarico ha una piastra perforata per regolare la portata. Fare clic qui per visualizzare una versione più grande di questa figura.
3. Analisi
- Per ogni angolo di inclinazione, tracciate i dati di pressione per entrambe le portate.
- Utilizzare i dati sperimentali per stimare la forza sulla piastra in base all'equazione (2).
- Determinare la velocità del getto alla vena contracta usando l'equazione (3).
- Stimare la portata massica utilizzando l'equazione (5).
Risultati
La Figura 4 mostra quattro serie di risultati ottenuti per il getto aereo che impatta su una piastra a due diverse angolazioni e due diverse portate. Infatti, poiché il lato a bassa pressione del trasduttore è aperto al ricevitore, le sue letture corrispondono solo alla 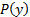 sovrapressione, che sono infatti i punti mostrati in Figura 4.
sovrapressione, che sono infatti i punti mostrati in Figura 4.
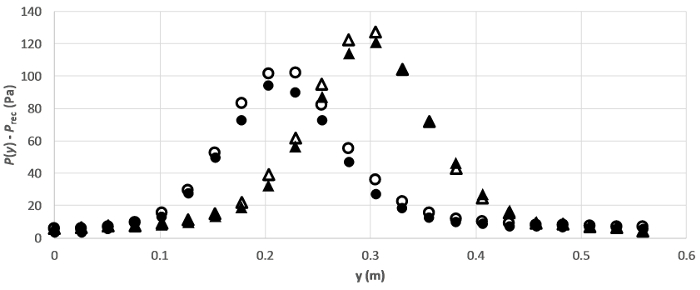
Figura 4. Risultati rappresentativi. Distribuzione della pressione lungo la piastra per due angoli e due portate. I simboli  rappresentano: :
rappresentano: : 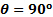 ,
, 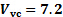 m/s;
m/s;  :
: 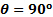 ,
,  m/s;
m/s;  :
:  ,
, 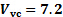 m/s;
m/s;  :
:  ,
,  m/s.
m/s.
Secondo la Figura 4, i profili per 90o impingement sono superiori a quelli per 70o impingement. La ragione di questo comportamento è che la linea di stagnazione per il primo caso corrisponde alla linea di mezzeria del flusso, cioè la linea di flusso per la velocità di picco e di conseguenza la pressione dinamica massima. Mentre la linea di stagnazione si allontana dalla linea di velocità di picco e si allontana dal suo percorso originale man mano che l'angolo di impingement diminuisce. Questo effetto è tracciato nella Figura 1(A) ed è anche il motivo per cui la pressione di picco nel profilo di pressione si allontana dal centro della piastra.
Come previsto, la pressione massima diminuisce con la portata (simboli chiusi in figura 4) perché c'è una riduzione generale dell'energia cinetica e quindi della pressione dinamica al diminuire della portata. Questa pressione massima è infatti una misura della pressione di ristagno,  precedentemente spiegata. Per il caso del getto che impatta la piastra a 90o, questa è una misura accurata di perché il rubinetto di
precedentemente spiegata. Per il caso del getto che impatta la piastra a 90o, questa è una misura accurata di perché il rubinetto di  pressione coincide con la linea di mezzeria, ergo la linea di ristagno, del getto. Ma come suggerito nella figura 1a, la streamline di stagnazione si allontana dal suo percorso originale man mano che l'angolo di impingement diminuisce. In questa nuova condizione, non vi è alcuna garanzia che questa streamline coincida esattamente con un rubinetto a pressione nella sua posizione di impingement. Quindi, la pressione di picco osservata ad angoli di impingement diversi da 90o è solo un'approssimazione a
pressione coincide con la linea di mezzeria, ergo la linea di ristagno, del getto. Ma come suggerito nella figura 1a, la streamline di stagnazione si allontana dal suo percorso originale man mano che l'angolo di impingement diminuisce. In questa nuova condizione, non vi è alcuna garanzia che questa streamline coincida esattamente con un rubinetto a pressione nella sua posizione di impingement. Quindi, la pressione di picco osservata ad angoli di impingement diversi da 90o è solo un'approssimazione a  .
.
La tabella 2 mostra i risultati ottenuti nelle misurazioni sperimentali per due diversi angoli di imping e portate.
Tabella 2. Risultati rappresentativi.
| Parametro | Corsa 1 | Corsa 2 | Corsa 3 | Corsa 4 |
| Angolo della piastra (θ) | 90o | 90o | 70o | 70o |
| Lettura digitale multimetro (E) | 2,44 V | 2,33 V | 2,44 V | 2,28 V |
| Differenza di pressione (P_pl-P_rec) | 335,95 Pa | 320,80 Pa | 335,95 Pa | 313,92 Pa |
| Velocità alla vena contracta (V_VC) | 10,14 m/s | 9,91 m/s | 10,14 m/s | 9,81 m/s |
| Portata massisca ((m)) ̇ | 0,254 kg/s | 0,249 kg/s | 0,254 kg/s | 0,246 kg/s |
| Pressione di ristagno (P_o ) | 127,16 Pa | 121,19 Pa | 101,78 Pa | 94,31 Pa |
| Carico sulla piastra (F) | 16,84 N | 16,24 N | 14,11 N | 12,32 N |
Applicazione e Riepilogo
Gli esperimenti qui descritti hanno dimostrato l'interazione tra pressione e velocità per generare carichi negli oggetti mediante la conversione della pressione dinamica in pressione statica. Questi concetti sono stati dimostrati con un jet aereo che impatta su una piastra piana a due diverse angolazioni e due diverse portate. Gli esperimenti hanno chiaramente dimostrato che il carico è più alto nel punto di ristagno, dove tutta la pressione dinamica viene convertita in pressione statica, e la sua grandezza diminuisce man mano che il livello di conversione da dinamico a statico diminuisce in posizioni lontane dal punto di ristagno. L'angolo di incidenza ha l'effetto di ridurre il carico totale perché sposta la pressione di ristagno da quella coincidente con la velocità della linea di mezzeria (massima) a una linea di flusso che trasporta livelli più bassi di pressione dinamica.
Questi esperimenti servivano anche a dimostrare come determinare il carico totale sull'oggetto esposto al flusso integrando numericamente i dati ottenuti dai rubinetti di pressione. Inoltre, la conversione inversa della pressione statica in pressione dinamica è stata utilizzata anche per stimare la velocità e la portata massica del getto. Di conseguenza, l'interazione tra pressione e velocità può essere utilizzata per la diagnostica del flusso.
Un concetto che non è stato esplorato nel presente esperimento è la velocimetria di Pitot - sonde statiche. Si tratta di sonde che misurano direttamente la differenza tra il ristagno e le pressioni statiche, che è esattamente ciò che è stato usato nell'equazione (3) per determinare la velocità alla vena contracta. Si noti che, almeno nella piastra angolare da 90o, il rubinetto centrale a pressione è direttamente esposto al punto di ristagno, rendendolo una sonda pitot. Poiché il trasduttore di pressione confronta la pressione di ciascun rubinetto di pressione con la pressione del ricevitore, il risultato è una misurazione diretta di  . Al momento della sostituzione di questa misura nell'equazione (3), il risultato è la velocità di un punto sulla linea di stagnazione che è vicino al punto di ristagno ma ancora al di fuori del suo raggio di influenza. Questa misurazione è di uso limitato in questo esperimento perché la posizione esatta di quel punto sulla linea di stagnazione non è nota.
. Al momento della sostituzione di questa misura nell'equazione (3), il risultato è la velocità di un punto sulla linea di stagnazione che è vicino al punto di ristagno ma ancora al di fuori del suo raggio di influenza. Questa misurazione è di uso limitato in questo esperimento perché la posizione esatta di quel punto sulla linea di stagnazione non è nota.
Come accennato in precedenza, le misurazioni della pressione possono essere utilizzate per determinare la velocità del flusso. Nell'applicazione qui descritta,la variazione di pressione tra il plenum e il ricevitore è stata sufficiente per stimare la velocità media alla vena contracta . È stato anche detto che, per inciso, il rubinetto di pressione che coincide con il punto di ristagno è un tubo di Pitot che potrebbe essere utilizzato in combinazione con una sonda che rileva la pressione statica per determinare la velocità del flusso dall'equazione (3) (sostituendo 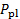 con e con
con e con 

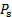 ). In effetti, un singolo dispositivo che combina una sonda di Pitot e una sonda statica, noto come tubo di Prandtl, potrebbe essere il dispositivo diagnostico più esteso nell'ingegneria dei fluidi per misurare la velocità. Come mostrato in figura 5, questa sonda è composta da due tubi concentrici. La camera d'aria è rivolta verso il flusso per rilevare la pressione di ristagno e il tubo esterno ha una serie di porte laterali che rilevano la pressione statica. Un sensore come un trasduttore di pressione o un manometro a colonna liquida viene utilizzato per determinare la differenza tra queste due pressioni per stimare la velocità dall'equazione (3) (di nuovo, sostituendo
). In effetti, un singolo dispositivo che combina una sonda di Pitot e una sonda statica, noto come tubo di Prandtl, potrebbe essere il dispositivo diagnostico più esteso nell'ingegneria dei fluidi per misurare la velocità. Come mostrato in figura 5, questa sonda è composta da due tubi concentrici. La camera d'aria è rivolta verso il flusso per rilevare la pressione di ristagno e il tubo esterno ha una serie di porte laterali che rilevano la pressione statica. Un sensore come un trasduttore di pressione o un manometro a colonna liquida viene utilizzato per determinare la differenza tra queste due pressioni per stimare la velocità dall'equazione (3) (di nuovo, sostituendo 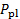 con
con  e con
e con 
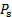 ). Una sonda come questa, o una combinazione di un Pitot e una sonda statica indipendente viene infatti utilizzata negli aeroplani per determinare la velocità del vento rispetto all'aereo.
). Una sonda come questa, o una combinazione di un Pitot e una sonda statica indipendente viene infatti utilizzata negli aeroplani per determinare la velocità del vento rispetto all'aereo.
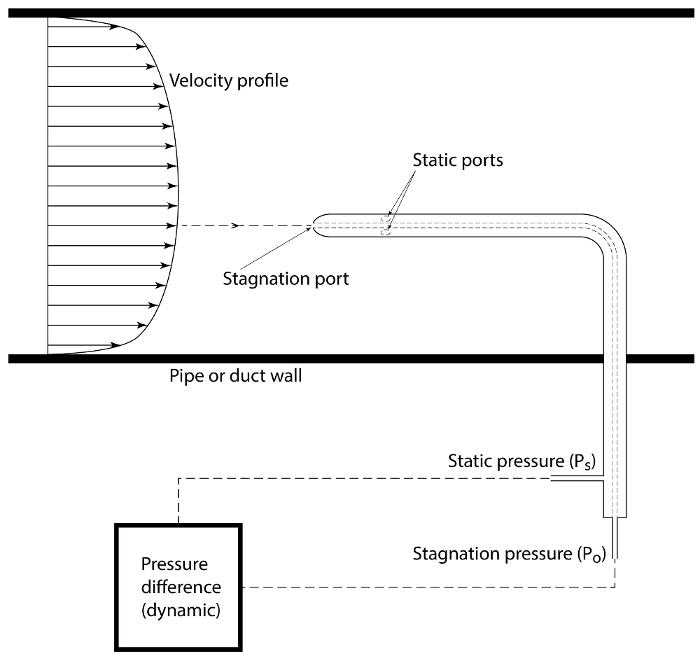
Figura 5. Velocimetria di flusso. Sonda pitot-statica (o Prandtl) per determinare la distribuzione della velocità in base alla pressione dinamica. Questa sonda viene attraversata attraverso il campo di flusso per determinare la velocità in diverse posizioni. Fare clic qui per visualizzare una versione più grande di questa figura.
Riferimenti
- Arnau, A. (ed.). Piezoelectric transducers and applications. Vol. 2004. Heidelberg: Springer, 2004.
- Tropea, C., A.L. Yarin, and J.F. Foss. Springer handbook of experimental fluid mechanics. Vol. 1. Springer Science & Business Media, 2007.
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Chapra, S.C. and R.P. Canale. Numerical methods for engineers. Vol. 2. New York: McGraw-Hill, 1998.
- Buckingham, E. Note on contraction coefficients of jets of gas. Journal of Research,6:765-775, 1931.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
- Lienhard V, J.H. and J.H. Lienhard IV. Velocity coefficients for free jets from sharp-edged orifices. ASME Journal of Fluids Engineering, 106:13-17, 1984.
Tags
Vai a...
Video da questa raccolta:

Now Playing
Getto che incide su una piastra inclinata
Mechanical Engineering
10.7K Visualizzazioni

Galleggiabilità e trascinamento su corpi immersi
Mechanical Engineering
29.9K Visualizzazioni

Stabilità dei vasi galleggianti
Mechanical Engineering
22.4K Visualizzazioni

Propulsione e spinta
Mechanical Engineering
21.6K Visualizzazioni

Reti di tubazioni e perdite di carico
Mechanical Engineering
58.0K Visualizzazioni

Raffreddamento ed ebollizione
Mechanical Engineering
7.7K Visualizzazioni

Salti idraulici
Mechanical Engineering
40.9K Visualizzazioni

Analisi dello scambiatore di calore
Mechanical Engineering
28.0K Visualizzazioni

Introduzione alla refrigerazione
Mechanical Engineering
24.6K Visualizzazioni

Anemometria a filo caldo
Mechanical Engineering
15.5K Visualizzazioni

Misurazione di flussi turbolenti
Mechanical Engineering
13.5K Visualizzazioni

Visualizzazione del flusso oltre un corpo Bluff
Mechanical Engineering
11.8K Visualizzazioni

Conservazione dell'energia come approccio all'analisi del sistema
Mechanical Engineering
7.4K Visualizzazioni

Conservazione di massa e misure di portata
Mechanical Engineering
22.6K Visualizzazioni

Determinazione delle forze di impingement su una piastra piana con il metodo del volume di controllo
Mechanical Engineering
26.0K Visualizzazioni