Jato Incidindo em uma Placa Inclinada
Visão Geral
Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Departamento de Engenharia Mecânica, Michigan State University, East Lansing, MI
O objetivo deste experimento é demonstrar como um fluxo fluido exerce forças sobre as estruturas por conversão de pressão dinâmica em pressão estática. Para isso, faremos um jato de avião em uma placa plana e mediremos a distribuição de pressão resultante ao longo da placa. A força resultante será estimada pela integração do produto entre a distribuição de pressão e diferenciais de área devidamente definidos ao longo da superfície da placa. Este experimento será repetido por dois ângulos de inclinação da placa em relação à direção do jato e duas taxas de fluxo. Cada configuração produz uma distribuição de pressão diferente ao longo da placa, que é o resultado de diferentes níveis de conversão de pressão dinâmica em pressão estática na superfície da placa.
Para este experimento, a pressão será medida com um transdutor de pressão diafragma conectado a uma válvula de varredura. A placa em si tem pequenas perfurações chamadas torneiras de pressão que se conectam à válvula de varredura através de mangueiras. A válvula de varredura envia a pressão dessas torneiras para o transdutor de pressão um de cada vez. A pressão induz a deflexão mecânica no diafragma que o transdutor de pressão converte em tensão. Esta tensão é proporcional à diferença de pressão entre os dois lados do diafragma.
Princípios
Em fluxos constantes incompressíveis com mudanças insignificantes no potencial gravitacional, a equação de Bernoulli poderia ser interpretada como a adição de duas formas de energia: energia cinética e energia potencial de pressão. Em um processo inviscid, essas formas de energia são livres para se transformarem entre si ao longo de aerodinâmicas, mantendo a quantidade total inicial de energia constante. Esse total de energia é chamado de constante de Bernoulli. Por conveniência, a equação de Bernoulli pode ser expressa em dimensões de pressão usando o princípio da homogeneidade dimensional [3]. Sob essa transformação dimensional, o termo associado à energia cinética é apelidado de "pressão dinâmica", o termo associado à energia potencial de pressão é chamado de "pressão estática", e a constante de Bernoulli é chamada de "pressão de estagnação". Este último pode ser interpretado como a pressão máxima que o fluxo alcançaria se parasse transformando toda a sua pressão dinâmica em pressão estática. Esses princípios podem ser melhor descritos pela seguinte forma da equação de Bernoulli:
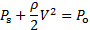 (1)
(1)
Onde 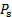 está a pressão estática, é a pressão
está a pressão estática, é a pressão  dinâmica, e é a pressão de
dinâmica, e é a pressão de  estagnação. A Figura 1(A) mostra um esquema do experimento atual. Como mostrado, um jato de ar sai de um plenário de maior pressão através de uma fenda de largura W e span L para um espaço fechado em uma pressão inferior chamada receptor. O receptor é uma pequena sala que serve como seção de teste para o experimento. Abriga os equipamentos de aquisição de dados e os experimentalistas. Depois de fluir por alguma distância, o jato se põe em uma placa plana dentro do receptor que faz um ângulo com o eixo do jato. O jato na figura 1(A) é delineado por três aerodinâmicas. A aerodinâmica intermediária divide o jato em duas regiões, uma que é desviada para cima e outra que é desviada para baixo. Uma vez que a divisão simplificada não é desviada, ela pára apenas na parede no que é conhecido como o ponto de estagnação. Nesse ponto, toda a pressão dinâmica é convertida em pressão estática e a pressão atinge seu nível máximo,
estagnação. A Figura 1(A) mostra um esquema do experimento atual. Como mostrado, um jato de ar sai de um plenário de maior pressão através de uma fenda de largura W e span L para um espaço fechado em uma pressão inferior chamada receptor. O receptor é uma pequena sala que serve como seção de teste para o experimento. Abriga os equipamentos de aquisição de dados e os experimentalistas. Depois de fluir por alguma distância, o jato se põe em uma placa plana dentro do receptor que faz um ângulo com o eixo do jato. O jato na figura 1(A) é delineado por três aerodinâmicas. A aerodinâmica intermediária divide o jato em duas regiões, uma que é desviada para cima e outra que é desviada para baixo. Uma vez que a divisão simplificada não é desviada, ela pára apenas na parede no que é conhecido como o ponto de estagnação. Nesse ponto, toda a pressão dinâmica é convertida em pressão estática e a pressão atinge seu nível máximo,  . O nível de pressão diminui para longe do ponto de estagnação porque progressivamente menos pressão dinâmica é convertida em pressão estática.
. O nível de pressão diminui para longe do ponto de estagnação porque progressivamente menos pressão dinâmica é convertida em pressão estática.
Dependendo do ângulo de impacto 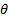 (na figura 1), a estagnação segue um caminho diferente. Quando
(na figura 1), a estagnação segue um caminho diferente. Quando  , a linha central do jato também é a estagnação simplificada. À medida
, a linha central do jato também é a estagnação simplificada. À medida 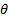 que diminui, a estagnação se afasta da linha central do jato, em direção a trajetórias que começam mais perto da borda externa do jato. Uma vez que 90o também é a trajetória de velocidade máxima, ergo máxima pressão dinâmica, seu ponto de estagnação resultante atingirá o valor máximo de pressão em comparação com outras trajetórias em valores menores de
que diminui, a estagnação se afasta da linha central do jato, em direção a trajetórias que começam mais perto da borda externa do jato. Uma vez que 90o também é a trajetória de velocidade máxima, ergo máxima pressão dinâmica, seu ponto de estagnação resultante atingirá o valor máximo de pressão em comparação com outras trajetórias em valores menores de 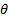 . Em resumo, o efeito do ângulo de impacto no perfil de pressão é reduzir seu valor máximo e deslocar seu pico para regiões da placa mais próximas da saída do jato.
. Em resumo, o efeito do ângulo de impacto no perfil de pressão é reduzir seu valor máximo e deslocar seu pico para regiões da placa mais próximas da saída do jato.
A linha tracejada na figura 1(A) representa a distribuição de pressão líquida ao longo da superfície da placa exposta ao jato. Note a partir da figura 1(B) que a pressão total na placa, 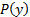 , é a adição da pressão circundante,
, é a adição da pressão circundante, 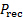 mais a pressão de impacto ou sobrepressão,
mais a pressão de impacto ou sobrepressão, 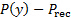 . Uma vez que a pressão circundante é distribuída de forma homogênea, ela cancela e a carga na placa é estritamente o resultado da sobrepressão. Esta distribuição de pressão será determinada experimentalmente e usada para estimar a carga líquida na placa de acordo com a seguinte integral:
. Uma vez que a pressão circundante é distribuída de forma homogênea, ela cancela e a carga na placa é estritamente o resultado da sobrepressão. Esta distribuição de pressão será determinada experimentalmente e usada para estimar a carga líquida na placa de acordo com a seguinte integral:
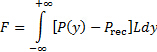 (2)
(2)
Uma vez que os dados experimentais são discretos, essa integral pode ser estimada usando a regra trapezoidal ou a regra do Simpson [4].
Além disso, quando os fluidos são descarregados de uma região de maior pressão para uma região de menor pressão através de orifícios ou fendas, o jato emissor tende a convergir inicialmente para uma região chamada vena contracta (ver Figura 1 para referência) e, em seguida, divergir depois disso à medida que flui para longe da porta de descarga [5]. A vena contracta é, na verdade, a primeira localização depois que um jato sai de seu porto de descarga no qual as aerodinâmicas se tornam paralelas. Consequentemente, este é o primeiro lugar ao longo do jato em que a pressão estática iguala a pressão do ambiente [5]. No presente experimento, o plenário é a região de maior pressão e o receptor é a região de menor pressão. Além disso, a velocidade dentro do plenário é insignificante, e pode ser considerada estagnada com aproximação muito boa. Assim, a equação (1) poderia ser usada para determinar a velocidade no contrato venada seguinte forma:
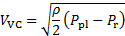 (3)
(3)
Aqui,  está a diferença de pressão entre o plenário e o receptor. Em geral, a razão de contração entre a largura da fenda e a contração vena é muito aproximadamente [5, 6, 7]:
está a diferença de pressão entre o plenário e o receptor. Em geral, a razão de contração entre a largura da fenda e a contração vena é muito aproximadamente [5, 6, 7]:
 (4)
(4)
Assim, a taxa de fluxo de massa pode ser estimada a partir de (3) e (4) da seguinte forma:
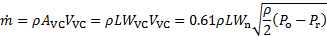 (5)
(5)
Aqui,  é a área da vena contracta.
é a área da vena contracta.

Figura 1. Esquema de configuração básica. Um jato de avião sai do plenário para dentro do receptor através de uma fenda de largura W. O jato se põe em uma placa inclinada e é desviado enquanto exerce uma carga de pressão na superfície (linha tracejada). Clique aqui para ver uma versão maior desta figura.
Procedimento
1. Definindo a instalação
- Certifique-se de que não há fluxo na instalação.
- Defina os instrumentos de acordo com o esquema na figura 2.
- Ajuste a placa ao ângulo desejado
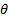 . Registo valor na tabela 1.
. Registo valor na tabela 1. - Meça a largura do bocal do jato W. Regisso valor na tabela 1.
- Meça o vão da placa L. Regisso valor na tabela 1.
- Zero o transdutor de pressão.
- Observe a constante de calibração do transdutor de pressão, mp (Pa/V). Registo valor na tabela 1.
- Conecte a porta de alta pressão do transdutor (marcada como +) à torneira de pressão do plenário (marcada como
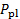 ).
). - Como todas as operações ocorrem dentro do receptor, deixe a porta de baixa pressão do transdutor (marcada como -) aberta para sentir a pressão no receptor (
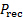 ).
). - Inicie a instalação de fluxo (FLL).
- Use o multi medidor digital para registrar a tensão
 (V) associada à diferença de pressão entre o plenário e o receptor sentido pelo transdutor de pressão. Registo valor na tabela 2.
(V) associada à diferença de pressão entre o plenário e o receptor sentido pelo transdutor de pressão. Registo valor na tabela 2. - Use a constante de calibração mp a partir de 1,7 para determinar a diferença de pressão entre o plenário e o receptor (
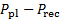 ). Registo este valor na tabela 2.
). Registo este valor na tabela 2.

Figura 2 . Detalhes do sistema de aquisição de dados. Esquema para conexões de equipamentos. Clique aqui para ver uma versão maior desta figura.
Tabela 1 . Parâmetros básicos para estudo experimental.
| Parâmetro | Valor |
| Largura do bocal do jato(Wn) | 41,3 mm |
| Extensão da placa(L) | 81,3 cm |
| Altura da placa(H) | 61cm |
| Constante de calibração do transdutor (m_p) | 137.6832 Pa/V |
2. Executando o experimento
- Conecte a porta de alta pressão do transdutor (marcado como +) à porta comum da válvula de varredura. Deixe a porta de baixa pressão do transdutor (marcada como -) aberta para sentir a pressão no receptor (
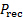 ).
). - Coloque a válvula de varredura para iniciar a medição a partir da primeira posição de toque de pressão.
- Execute o Traverse VI (instrumento virtual LabView).
- Insira a constante de calibração mp no VI.
- Defina a taxa de amostragem para 100 Hz e o total de amostras para 500 (ou seja, 5 segundos de dados).
- Digite no VI a posição (
 ) da torneira de pressão a partir da qual os dados de pressão da placa serão adquiridos. Leve em conta que as torneiras de pressão são espaçadas em 25,4 mm. Assim, a posição será
) da torneira de pressão a partir da qual os dados de pressão da placa serão adquiridos. Leve em conta que as torneiras de pressão são espaçadas em 25,4 mm. Assim, a posição será  mm, onde
mm, onde 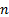 está o índice da torneira começando em 0.
está o índice da torneira começando em 0. - Regisso. O VI lerá a diferença de pressão entre a torneira de pressão e o receptor (
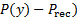 .
. - Pise a válvula de varredura para a próxima posição de torneira.
- Repita as etapas 2.6 a 2.8 até que todas as torneiras de pressão sejam atravessadas.
- No final, o VI fornece uma tabela e um gráfico de posição de toque versus pressão.
- Pare o VI.
- Altere a posição da placa de controle de fluxo para fechar a área de fluxo aproximadamente pela metade (ver Figura 3 para referência). Isso modificará a taxa de fluxo. Use a Equação (5) para determinar o valor dessa taxa de fluxo.
- Repita as etapas 2.3 a 2.11 para a nova posição da placa de controle de fluxo.
- Modifique o ângulo da placa de impacto e coloque a placa de controle de fluxo na posição inicial.
- Repetir passos 2.3 a 2.14 para 80o, 70o, 60o, 50o, e 45o.

Figura 3 . Configuração experimental. Seção de teste. Esquerda: Placa de impacto na frente da fenda. O ar de maior pressão é descarregado do plenário para o receptor através desta fenda. Meio: as torneiras de pressão conectadas à placa de impacto são distribuídas na válvula de varredura para amostrar uma de cada vez. Direito: placa de impacto na frente da descarga do receptor. A descarga tem uma placa perfurada para regular a taxa de fluxo. Clique aqui para ver uma versão maior desta figura.
3. Análise
- Para cada ângulo de inclinação, plote os dados de pressão para ambas as taxas de fluxo.
- Use os dados experimentais para estimar a força na placa com base na equação (2).
- Determine a velocidade do jato na vena contracta usando equação (3).
- Estime a taxa de fluxo de massa usando equação (5).
Resultados
A Figura 4 mostra quatro conjuntos de resultados obtidos para o jato de avião que se impõe em uma placa em dois ângulos diferentes e duas taxas de fluxo diferentes. De fato, uma vez que o lado de baixa pressão do transdutor é aberto ao receptor, suas leituras correspondem apenas à sobrepressão 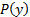 , que são de fato os pontos mostrados na Figura 4.
, que são de fato os pontos mostrados na Figura 4.
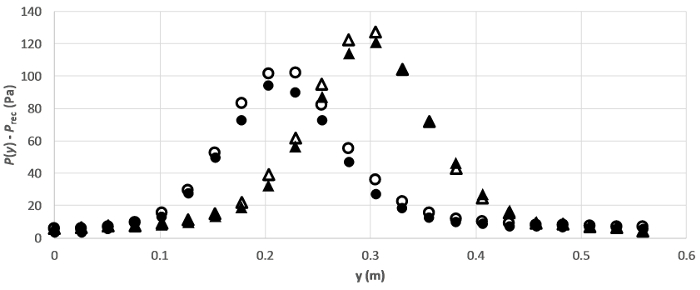
Figura 4. Resultados representativos. Distribuição de pressão ao longo da placa para dois ângulos e duas taxas de fluxo. Os símbolos representam:  :
: 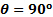 ,
, 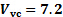 m/s;
m/s;  :
: 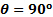 ,
,  m/s;
m/s;  :
:  ,
, 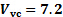 m/s;
m/s;  :
:  ,
,  m/s.
m/s.
De acordo com a Figura 4,os perfis para 90o impacto são superiores aos de 70o impacto. A razão para esse comportamento é que a estagnação simplificada para o primeiro caso corresponde à linha central de fluxo, ou seja, a simplificação para velocidade máxima e, consequentemente, máxima pressão dinâmica. Enquanto a estagnação se afasta da linha de velocidade máxima e se curva para longe de seu caminho original à medida que o ângulo de impacto diminui. Este efeito é esboçado na Figura 1(A), e também é a razão pela qual a pressão máxima no perfil de pressão se afasta do centro da placa.
Como esperado, a pressão máxima diminui com a taxa de fluxo (símbolos fechados na figura 4) porque há uma redução geral da energia cinética e, portanto, na pressão dinâmica à medida que a taxa de fluxo diminui. Essa pressão máxima é, na verdade, uma medida da pressão de  estagnação, explicada anteriormente. Para o caso do jato que impinge a placa a 90o, esta é uma medida precisa de porque a torneira de
estagnação, explicada anteriormente. Para o caso do jato que impinge a placa a 90o, esta é uma medida precisa de porque a torneira de  pressão coincide com a linha central, ergo a estagnação simplificada, do jato. Mas, como sugerido na figura 1a, a estagnação se curva para longe de seu caminho original à medida que o ângulo de impacto diminui. Sob esta nova condição, não há garantia de que essa simplificação coincidirá exatamente com uma torneira de pressão em seu local de impacto. Assim, a pressão máxima observada em ângulos de impacto diferentes de 90o é apenas uma aproximação para
pressão coincide com a linha central, ergo a estagnação simplificada, do jato. Mas, como sugerido na figura 1a, a estagnação se curva para longe de seu caminho original à medida que o ângulo de impacto diminui. Sob esta nova condição, não há garantia de que essa simplificação coincidirá exatamente com uma torneira de pressão em seu local de impacto. Assim, a pressão máxima observada em ângulos de impacto diferentes de 90o é apenas uma aproximação para  .
.
A Tabela 2 mostra os resultados obtidos em medições experimentais para dois ângulos e taxas de fluxo diferentes.
Tabela 2. Resultados representativos.
| Parâmetro | Corrida 1 | Corrida 2 | Corrida 3 | Corrida 4 |
| Ângulo da placa (φ) | 90o | 90o | 70o | 70o |
| Leitura digital de vários medidores (E) | 2,44 V | 2,33 V | 2,44 V | 2,28 V |
| Diferença de pressão (P_pl-P_rec ) | 335.95 Pa | 320,80 Pa | 335.95 Pa | 313.92 Pa |
| Velocidade em vena contracta (V_VC) | 10,14 m/s | 9,91 m/s | 10,14 m/s | 9,81 m/s |
| Taxa de fluxo de massa ((m)) | 0,254 kg/s | 0,249 kg/s | 0,254 kg/s | 0,246 kg/s |
| Pressão de estagnação (P_o) | 127.16 Pa | 121.19 Pa | 101.78 Pa | 94.31 Pa |
| Carga na placa(F) | 16.84 N | 16.24 N | 14.11 N | 12.32 N |
Aplicação e Resumo
Os experimentos aqui apresentados demonstraram a interação de pressão e velocidade para gerar cargas em objetos por meio da conversão da pressão dinâmica em pressão estática. Esses conceitos foram demonstrados com um jato de avião batendo em uma placa plana em dois ângulos diferentes e duas taxas de fluxo diferentes. Os experimentos demonstraram claramente que a carga é mais alta no ponto de estagnação, onde toda a pressão dinâmica é convertida em pressão estática, e sua magnitude diminui à medida que o nível de conversão da dinâmica para a estática diminui em posições distantes do ponto de estagnação. O ângulo de incidência tem o efeito de reduzir a carga total porque muda a pressão de estagnação da coincidindo com a velocidade central (máxima) para uma simplificação carregando níveis mais baixos de pressão dinâmica.
Esses experimentos também serviram com o propósito de demonstrar como determinar a carga total no objeto exposto ao fluxo, integrando numericamente os dados obtidos a partir de torneiras de pressão. Além disso, a conversão reversa da pressão estática em pressão dinâmica também foi usada para estimar a velocidade e a taxa de fluxo de massa do jato. Em consequência, a interação entre pressão e velocidade pode ser usada para diagnósticos de fluxo.
Um conceito que não foi explorado no presente experimento é a velocimetria por Pitot - sondas estáticas. Estas são sondas que medem diretamente a diferença entre a estagnação e as pressões estáticas, que é exatamente o que foi usado na equação (3) para determinar a velocidade na vena contracta. Note que, pelo menos na placa angular de 90o, a torneira de pressão central está diretamente exposta ao ponto de estagnação, tornando-a uma sonda Pitot. Uma vez que o transdutor de pressão compara a pressão de cada toque de pressão à pressão do receptor, o resultado é uma medição direta de  . Após a substituição desta medição na equação (3), o resultado é a velocidade de um ponto na simplificação da estagnação que está perto do ponto de estagnação, mas ainda fora de seu raio de influência. Esta medição é de uso limitado neste experimento porque a localização exata desse ponto na simplificação da estagnação não é conhecida.
. Após a substituição desta medição na equação (3), o resultado é a velocidade de um ponto na simplificação da estagnação que está perto do ponto de estagnação, mas ainda fora de seu raio de influência. Esta medição é de uso limitado neste experimento porque a localização exata desse ponto na simplificação da estagnação não é conhecida.
Como mencionado anteriormente, medidas de pressão podem ser usadas para determinar a velocidade de fluxo. Na aplicação aqui descrita, a mudança de pressão entre o plenário e o receptor foi suficiente para estimar a velocidade média na vena contracta. Também foi mencionado que, aliás, a torneira de pressão coincidindo com o ponto de estagnação é um tubo Pitot que poderia ser usado em conjunto com uma sonda detectando a pressão estática para determinar a velocidade de fluxo da equação (3) (substituindo com e com 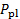


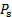 ). Na verdade, um único dispositivo combinando uma sonda Pitot e uma sonda estática, conhecida como tubo Prandtl, pode ser o dispositivo de diagnóstico mais estendido na engenharia de fluidos para medir a velocidade. Como mostrado na figura 5, esta sonda é composta por dois tubos concêntricos. O tubo interno enfrenta o fluxo para detectar a pressão de estagnação, e o tubo externo tem um conjunto de portas laterais que sentem a pressão estática. Um sensor como um transdutor de pressão ou um manômetro de coluna líquida é usado para determinar a diferença entre essas duas pressões para estimar a velocidade da equação (3) (novamente, substituindo
). Na verdade, um único dispositivo combinando uma sonda Pitot e uma sonda estática, conhecida como tubo Prandtl, pode ser o dispositivo de diagnóstico mais estendido na engenharia de fluidos para medir a velocidade. Como mostrado na figura 5, esta sonda é composta por dois tubos concêntricos. O tubo interno enfrenta o fluxo para detectar a pressão de estagnação, e o tubo externo tem um conjunto de portas laterais que sentem a pressão estática. Um sensor como um transdutor de pressão ou um manômetro de coluna líquida é usado para determinar a diferença entre essas duas pressões para estimar a velocidade da equação (3) (novamente, substituindo 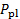 com
com  e com
e com 
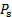 ). Uma sonda como esta, ou uma combinação de um Pitot e uma sonda estática independente é de fato usada em aviões para determinar a velocidade do vento em relação ao avião.
). Uma sonda como esta, ou uma combinação de um Pitot e uma sonda estática independente é de fato usada em aviões para determinar a velocidade do vento em relação ao avião.
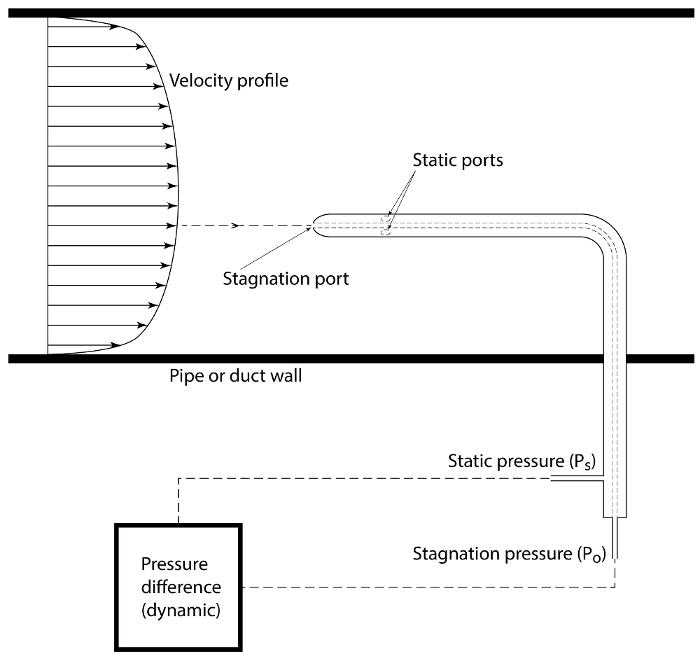
Figura 5. Velocimetria de fluxo. Sonda pitot-estática (ou Prandtl) para determinar a distribuição de velocidade com base na pressão dinâmica. Esta sonda é atravessada pelo campo de fluxo para determinar a velocidade em diferentes posições. Clique aqui para ver uma versão maior desta figura.
Referências
- Arnau, A. (ed.). Piezoelectric transducers and applications. Vol. 2004. Heidelberg: Springer, 2004.
- Tropea, C., A.L. Yarin, and J.F. Foss. Springer handbook of experimental fluid mechanics. Vol. 1. Springer Science & Business Media, 2007.
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Chapra, S.C. and R.P. Canale. Numerical methods for engineers. Vol. 2. New York: McGraw-Hill, 1998.
- Buckingham, E. Note on contraction coefficients of jets of gas. Journal of Research,6:765-775, 1931.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
- Lienhard V, J.H. and J.H. Lienhard IV. Velocity coefficients for free jets from sharp-edged orifices. ASME Journal of Fluids Engineering, 106:13-17, 1984.
Tags
Pular para...
Vídeos desta coleção:

Now Playing
Jato Incidindo em uma Placa Inclinada
Mechanical Engineering
10.7K Visualizações

Empuxo e Arrasto em Corpos Imersos
Mechanical Engineering
29.9K Visualizações

Estabilidade de Embarcações Flutuantes
Mechanical Engineering
22.4K Visualizações

Propulsão e Impulso
Mechanical Engineering
21.6K Visualizações

Redes de tubulação e perdas de pressão
Mechanical Engineering
58.0K Visualizações

Resfriamento e Ebulição
Mechanical Engineering
7.7K Visualizações

Saltos Hidráulicos
Mechanical Engineering
40.9K Visualizações

Análise de Trocadores de Calor
Mechanical Engineering
28.0K Visualizações

Introdução à Refrigeração
Mechanical Engineering
24.6K Visualizações

Anemometria com fio quente
Mechanical Engineering
15.5K Visualizações

Medindo fluxos turbulentos
Mechanical Engineering
13.5K Visualizações

Visualização do Fluxo ao Redor de um Corpo Parado
Mechanical Engineering
11.8K Visualizações

Abordagem de Conservação de Energia para Análise de Sistemas
Mechanical Engineering
7.4K Visualizações

Conservação de Massa e Medições de Taxa de Fluxo
Mechanical Engineering
22.6K Visualizações

Determinação das Forças de Impacto em uma Placa Plana com o Método do Volume de Controle
Mechanical Engineering
26.0K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados