Conservação de Massa e Medições de Taxa de Fluxo
Visão Geral
Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Departamento de Engenharia Mecânica, Michigan State University, East Lansing, MI
O objetivo deste experimento é demonstrar a calibração de uma passagem de fluxo como um medidor de fluxo usando uma formulação de volume de controle (CV) [1, 2]. A análise cv se concentra no efeito macroscópico do fluxo nos sistemas de engenharia, em vez da descrição detalhada que poderia ser alcançada com uma análise diferencial detalhada. Essas duas técnicas devem ser consideradas abordagens complementares, pois a análise cv dará ao engenheiro uma base inicial sobre qual caminho seguir ao projetar um sistema de fluxo. Em linhas gerais, uma análise de CV dará ao engenheiro uma ideia da troca de massa dominante em um sistema, e deve ser idealmente o passo inicial a ser dados antes de buscar qualquer projeto ou análise detalhado através de formulação diferencial.
O principal princípio por trás da formulação cv para conservação de massa é substituir os detalhes de um sistema de fluxo por um volume simplificado fechado no que é conhecido como superfície de controle (CS). Esse conceito é imaginário e pode ser definido livremente para simplificar a análise de forma inteligente. Por exemplo, o CS deve 'cortar' portas de entrada e saída em uma direção perpendicular à velocidade dominante. Em seguida, a análise consistiria em encontrar o equilíbrio entre o fluxo de massa líquido através do CS e a taxa de mudança de massa dentro do CV. Esta técnica será demonstrada com a calibração de uma contração suave como um medidor de fluxo.
Princípios
Um volume de controle (CV) é definido por uma superfície fechada imaginária, apelidada de superfície de controle (CS), definida arbitrariamente para estudar o equilíbrio de massa em um sistema. A Figura 1A mostra um exemplo de um volume de controle contendo uma região de fluxo passando por uma passagem de fluxo. Os detalhes do fluxo na passagem são irrelevantes, pois estamos meramente interessados em obter medidas da entrada em massa, do fluxo de saída e de sua taxa de mudança dentro da passagem de fluxo. Todos esses efeitos podem ser resumidos na equação para conservação da massa na forma integral [1, 2]:
 (1)
(1)
O primeiro termo no lado direito da equação (1) representa a taxa de mudança de massa dentro do volume de controle, enquanto o segundo termo representa o fluxo líquido de massa através da superfície de controle. A diferença vetorial 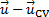 é a velocidade relativa entre o CV e o fluxo, e o vetor
é a velocidade relativa entre o CV e o fluxo, e o vetor  é a unidade externa normal para o diferencial da área. O produto ponto entre a velocidade relativa e
é a unidade externa normal para o diferencial da área. O produto ponto entre a velocidade relativa e  representa o componente de velocidade que cruza o CS, e a partir de agora contribui para a troca de massa. O sinal deste produto ponto é negativo onde o fluxo de massa é direcionado para o CV e positivo onde é direcionado para longe do CV.
representa o componente de velocidade que cruza o CS, e a partir de agora contribui para a troca de massa. O sinal deste produto ponto é negativo onde o fluxo de massa é direcionado para o CV e positivo onde é direcionado para longe do CV.

Figura 1. Schematic de configuração básica. (A) Entrada suave para um ventilador centrífuga. O volume de controle é definido como o perfil interno da passagem. As paredes sólidas são excluídas do volume de controle, mas suas condições de limite são mantidas na superfície de controle (ou seja, sem penetração e sem deslizamento). A porta 1 é definida como o lado de entrada da passagem, enquanto a porta 2 é definida como o plano transversal que coincide com a ponta do tubo Pitot. O fluxo vai da esquerda para a direita. (B) Sistema estático pitot e schematic do sistema de aquisição de dados. Por favor, clique aqui para ver uma versão maior desta figura.
Para a presente demonstração, temos as configurações mostradas na Figura 1A, onde um CV fixo segue o contorno de como contração suave na entrada de um ventilador centrífuga. O fluxo através deste CV é constante, portanto a taxa de variação de massa dentro do volume de controle é zero. Assim, o primeiro termo no lado direito da equação (1) desaparece. Além disso, o CV é anexado à contração, que é fixada no espaço e não tem velocidade, fazendo 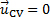 . Portanto, o fluxo líquido de massa através deste CV é zero e a equação (1) simplifica para:
. Portanto, o fluxo líquido de massa através deste CV é zero e a equação (1) simplifica para:
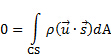 (2)
(2)
Considerando a configuração na Figura 1A, a massa flui para o CV através da porta 1 e deixa o CV através da porta 2. Consequentemente, a integral superficial no lado direito da equação (2) pode ser dividida em duas integrais independentes, uma para cada porta. O sinal do produto ponto é negativo na porta 1 porque o fluxo vai em direção ao CV, e positivo na porta 2 porque o fluxo vai para longe do CV. Sem assumir que a velocidade é distribuída de forma homogênea em ambas as portas, vamos fazer 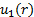 e
e 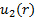 os respectivos perfis de velocidade levando em conta que ambos são o que permanecem após tomar o produto ponto. Ou seja, a magnitude do componente de velocidade paralelo ao vetor da área,
os respectivos perfis de velocidade levando em conta que ambos são o que permanecem após tomar o produto ponto. Ou seja, a magnitude do componente de velocidade paralelo ao vetor da área,  . Finalmente, as mudanças de pressão ao longo da contração não são significativas o suficiente para induzir mudanças observáveis na densidade. De agora em diante, podemos considerar a densidade como constante. Nestas circunstâncias, a equação (2) simplificaria para:
. Finalmente, as mudanças de pressão ao longo da contração não são significativas o suficiente para induzir mudanças observáveis na densidade. De agora em diante, podemos considerar a densidade como constante. Nestas circunstâncias, a equação (2) simplificaria para:
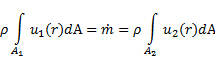 (3)
(3)
Note que, uma vez que a massa é conservada, o fluxo de massa,  é o mesmo através de ambas as portas. Dada a estrutura dessas relações, cada integral na equação (3) expressa a taxa de fluxo volumoso,
é o mesmo através de ambas as portas. Dada a estrutura dessas relações, cada integral na equação (3) expressa a taxa de fluxo volumoso,  através de sua porta correspondente, e este fato ajuda a definir a velocidade média, para uma determinada
através de sua porta correspondente, e este fato ajuda a definir a velocidade média, para uma determinada 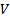 porta:
porta:
 (4)
(4)
Em condições inviscidas, a velocidade na porta 2 poderia ser expressa em termos das condições fora da entrada usando a equação de Bernoulli ao longo da simplificação central (ver Figura 1A para referência):
 (5)
(5)
Aqui, o efeito da altura desaparece na aerodinâmica central porque é horizontal, e é insignificante nas outras aerodinâmicas porque o fluido é o ar, que tem um peso específico muito pequeno. Além disso, o ponto inicial na aerodinâmica central está suficientemente longe da entrada que sua velocidade é zero. Dado que a equação (5) é para o caso inviscid idealizado, este valor de velocidade será o mesmo em toda a porta 2. Na realidade, o crescimento da camada de fronteira afeta o perfil de velocidade e o torna não homogêneo. Para explicar esse efeito, a estimativa ideal é comparada com as medições experimentais através do "Coeficiente de Descarga". Este coeficiente é definido como a razão entre a velocidade média medida e a velocidade inviscd para uma determinada seção transversal do fluxo:
 (6)
(6)
O coeficiente de  descarga, depende da geometria e do número de Reynolds. Uma vez determinado,
descarga, depende da geometria e do número de Reynolds. Uma vez determinado,  poderia ser usado em conjunto com equações (4) e (5) para determinar a taxa de fluxo através da porta 2 com base em sua área transversal e um diferencial de pressão fácil de medir:
poderia ser usado em conjunto com equações (4) e (5) para determinar a taxa de fluxo através da porta 2 com base em sua área transversal e um diferencial de pressão fácil de medir:
 (7)
(7)
Ao colocar equações (4), (5) e (6) juntas, e considerando que a porta 2 é circular, obtemos a seguinte relação  para:
para:
 (8)
(8)
Fica claro a partir da equação (8) que o conhecimento do perfil de velocidade é necessário para obter o coeficiente de descarga. Para isso, usaremos a velocimetria por Pitot - sondas estáticas. Como mostrado na Figura 1B, o tubo Pitot traz o fluxo para parar de sentir a pressão total, 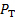 que é a adição das pressões estáticas e dinâmicas em um determinado ponto. Por outro lado, a sonda estática na parede detecta a pressão estática sozinha. Da equação de Bernoulli aplicada em uma determinada posição radial, a pressão total é apenas a constante de Bernoulli. No porto 2, este princípio pode ser expresso pela seguinte relação em posição radial arbitrária:
que é a adição das pressões estáticas e dinâmicas em um determinado ponto. Por outro lado, a sonda estática na parede detecta a pressão estática sozinha. Da equação de Bernoulli aplicada em uma determinada posição radial, a pressão total é apenas a constante de Bernoulli. No porto 2, este princípio pode ser expresso pela seguinte relação em posição radial arbitrária:
 (9)
(9)
Aqui, estamos negligenciando o efeito da posição vertical porque nossa passagem de fluxo é horizontal. Em resumo, obtém-se a seguinte relação para a magnitude da velocidade em uma determinada posição 'r' dentro do tubo:
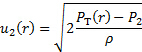 (10)
(10)
A diferença de pressão  é diretamente medida pelo transdutor de pressão retratado na Figura 1B, e o perfil de velocidade é obtido atravessando o tubo Pitot ao longo da coordenada radial do tubo. Observe que essas medidas de velocidade são realizadas em posições discretas, portanto, esses pontos de dados devem ser usados para resolver a integral na equação (8) numericamente usando o trapezoidal ou a regra do Simpson [1]. Uma vez obtido o valor desta integral, ele deve ser conectado à equação (8) juntamente com o valor medido de
é diretamente medida pelo transdutor de pressão retratado na Figura 1B, e o perfil de velocidade é obtido atravessando o tubo Pitot ao longo da coordenada radial do tubo. Observe que essas medidas de velocidade são realizadas em posições discretas, portanto, esses pontos de dados devem ser usados para resolver a integral na equação (8) numericamente usando o trapezoidal ou a regra do Simpson [1]. Uma vez obtido o valor desta integral, ele deve ser conectado à equação (8) juntamente com o valor medido de  , a densidade e o raio do duto, para obter o valor dessa condição de fluxo
, a densidade e o raio do duto, para obter o valor dessa condição de fluxo  particular. Ao repetir este experimento para diferentes condições de fluxo, obteremos um gráfico de dispersão que poderia ser usado para determinar uma relação entre
particular. Ao repetir este experimento para diferentes condições de fluxo, obteremos um gráfico de dispersão que poderia ser usado para determinar uma relação entre  e
e  . Essa relação pode então ser substituída na equação (7) para determinar totalmente a taxa de fluxo,
. Essa relação pode então ser substituída na equação (7) para determinar totalmente a taxa de fluxo,  em função apenas de
em função apenas de  .
.
Procedimento
1. Definindo a instalação
- Certifique-se de que não há fluxo na instalação.
- Verifique se o sistema de aquisição de dados segue o esquema na Figura 1B.
- Conecte a porta positiva do transdutor de pressão #1 (ver Figura 1B para referência) ao tubo Pitot transversal (
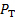 ).
). - Conecte a porta negativa deste mesmo transdutor de pressão à sonda estática da passagem de admissão (
 ). Assim, a leitura desse transdutor de pressão será direta (
). Assim, a leitura desse transdutor de pressão será direta (  ).
). - Registo do transdutor de Volts para Pascals (
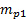 ). Digite este valor na Tabela 1.
). Digite este valor na Tabela 1. - Conecte a porta positiva do transdutor de pressão #2 (ver Figura 1B para referência) à sonda estática da passagem de admissão (
 ) usando um tee.
) usando um tee. - Deixe a porta negativa de transdutor de pressão #2 aberta à atmosfera (
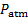 ). Assim, a leitura deste transdutor será direta (
). Assim, a leitura deste transdutor será direta (  ).
). - Registo do transdutor de Volts para Pascals (
 ). Digite este valor na Tabela 1.
). Digite este valor na Tabela 1. - Defina o sistema de aquisição de dados para amostrar a uma taxa de 100 Hz para um total de 500 amostras (ou seja, 5s de dados).
- Certifique-se de que o canal 1 no sistema de aquisição de dados corresponde à #1 de transdutor de pressão (
 ).
). - Digite o fator de conversão
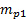 no sistema de aquisição de dados para garantir que a medição de pressão ( ) seja
no sistema de aquisição de dados para garantir que a medição de pressão ( ) seja  diretamente convertida para Pascal.
diretamente convertida para Pascal. - Coloque a sonda Pitot no final de sua viagem, onde ela toca a parede do tubo. Como a sonda tem 2 mm de diâmetro, o primeiro ponto de velocidade está em uma coordenada radial a 1 mm de distância da parede. Ou seja, em uma posição radial de
 mm (aqui,
mm (aqui,  mm).
mm).

Figura 2. Configuração experimental. (A): Passagem de fluxo em estudo. (B): sistema de travessia manual para o tubo Pitot. Clique aqui para ver uma versão maior desta figura.
Mesa 1. Parâmetros básicos para estudo experimental. Valor do ameter de par
| Parâmetro | Valor |
| Raio de passagem de fluxo(Ro) | 82,25 mm |
| Constante de calibração de #1 transdutor (m_p1) | 136.015944 Pa/V |
| Constante de calibração #2 transdutor (m_p2) | 141.241584 N/V |
| Pressão atmosférica local | 100.474,15 Pa |
| Temperatura local | 297,15 K |
| P_atm-P_2 | 311.01 Pa |
2. Medições
- Ligue a instalação de fluxo.
- Registo a leitura do transdutor de pressão #2 em Volts a partir do multimetro digital.
- Digite este valor na Tabela 1 como
 e converta a leitura de Volts para Pascals usando o fator
e converta a leitura de Volts para Pascals usando o fator  .
. - Use o sistema de aquisição de dados para registrar a leitura de (
 .
. - Digite o valor da
 Tabela 2.
Tabela 2. - Use o botão de travessia para alterar a posição radial do tubo Pitot de acordo com o valor sugerido na Tabela 2.
- Repita as etapas 2.4 e 2.6 até que a Tabela 2 esteja totalmente povoada.
- Altere a taxa de fluxo variando a descarga do sistema.
- Repita as etapas 2.4 a 2.8 para pelo menos dez taxas de fluxo diferentes.
- Desligue a instalação de fluxo.

Figura 5. Configuração experimental. Placas perfuradas para restringir o fluxo na descarga do sistema de fluxo. Clique aqui para ver uma versão maior desta figura.
Mesa 2. Resultados representativos. Medições de velocidade. r (mm) PT - P2 (Pa) u (r) (m/s
| r (mm) | PT - P2 (Pa) | u(r) (m/s) |
| 2.25 | 300.35 | 22.34 |
| 12.25 | 302.84 | 22.43 |
| 22.25 | 305.82 | 22.54 |
| 32.25 | 302.34 | 22.41 |
| 42.25 | 294.88 | 22.13 |
| 52.25 | 295.37 | 22.15 |
| 62.25 | 292.88 | 22.06 |
| 68.25 | 293.63 | 22.09 |
| 72.25 | 294.13 | 22.10 |
| 75.25 | 299.60 | 22.31 |
| 77.25 | 293.13 | 22.07 |
| 79.25 | 284.67 | 21.75 |
| 80.25 | 256.31 | 20.63 |
| 81.25 | 198.33 | 18.15 |
3. Análise de dados.
- Determine o perfil de velocidade usando os valores de diferença de pressão, PT - P2, da Tabela 2. Digite os resultados na Tabela 2.
- Plote os valores de pressão e velocidade da Tabela 2 utilizando o raio,
 como as abscissas(Figura 3).
como as abscissas(Figura 3). - Calcule a integral na equação (8) com base nos valores de velocidade e raio da Tabela 2.
- Calcule o coeficiente de descarga para cada taxa de fluxo usando equação (8).
- Plote o coeficiente de descarga usando
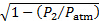 como abscissas.
como abscissas. - Encaixar uma função no coeficiente de descarga, uma lei de poder é uma boa escolha.

Figura 3. Resultados representativos. (A): Exemplo de medição da pressão estática ao longo da coordenada radial da passagem de fluxo. (B): Distribuição de velocidade determinada a partir das medições da pressão estática. Clique aqui para ver uma versão maior desta figura.
Resultados
Para uma dada restrição do fluxo na descarga do ventilador, a Figura 3A mostra as medidas de pressão dinâmica (  ) em diferentes locais radiais dentro do tubo após atravessar com o tubo Pitot. Esses valores foram utilizados para determinar a velocidade local nesses locais radiais, e os resultados são mostrados na Figura 3B. Depois de usar a regra trapezoidal sobre esses dados para resolver a equação (4) para a velocidade média, obtivemos um valor de
) em diferentes locais radiais dentro do tubo após atravessar com o tubo Pitot. Esses valores foram utilizados para determinar a velocidade local nesses locais radiais, e os resultados são mostrados na Figura 3B. Depois de usar a regra trapezoidal sobre esses dados para resolver a equação (4) para a velocidade média, obtivemos um valor de  m/s. Por outro lado, o valor
m/s. Por outro lado, o valor  da Tabela 1 foi utilizado para determinar a velocidade ideal da equação (5):
da Tabela 1 foi utilizado para determinar a velocidade ideal da equação (5):  m/s. Assim, o coeficiente de descarga para esta condição de fluxo é:
m/s. Assim, o coeficiente de descarga para esta condição de fluxo é: 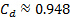 . Este valor é mostrado na Figura 4 como um triângulo vermelho.
. Este valor é mostrado na Figura 4 como um triângulo vermelho.
Depois de repetir este experimento mais vinte e nove vezes, obtivemos o gráfico de dispersão mostrado na Figura 4. Esses dados podem ser bem representados por uma lei de poder 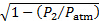 de:
de:
 (11)
(11)
A razão para essa escolha de argumento é garantir que a constante líder permaneça a dimensionada e, portanto, essa correlação ainda seria válida independentemente do sistema de unidades utilizadas para a pressão. Esta função pode ser substituída na equação (7) para obter a taxa de fluxo em função de  :
:
 (12)
(12)
Aqui, todas as constantes das equações (7) e (11) foram agrupadas em uma única constante abrental:  . Consequentemente, a equação (12) é válida para qualquer sistema de unidades, desde que as variáveis sejam consistentemente atribuídas às unidades correspondentes. Por conveniência, a densidade da equação (7) foi expressa em termos de pressão atmosférica e temperatura absoluta usando a lei do gás ideal. A equação (12) é válida para diferentes condições atmosféricas, pois contabiliza mudanças na pressão e temperatura local(T e Patm). Além disso, enquanto a similaridade geométrica for conservada, esta equação seria válida para passagens de diferentes tamanhos, conforme contabilizado pelo raio R.
. Consequentemente, a equação (12) é válida para qualquer sistema de unidades, desde que as variáveis sejam consistentemente atribuídas às unidades correspondentes. Por conveniência, a densidade da equação (7) foi expressa em termos de pressão atmosférica e temperatura absoluta usando a lei do gás ideal. A equação (12) é válida para diferentes condições atmosféricas, pois contabiliza mudanças na pressão e temperatura local(T e Patm). Além disso, enquanto a similaridade geométrica for conservada, esta equação seria válida para passagens de diferentes tamanhos, conforme contabilizado pelo raio R.
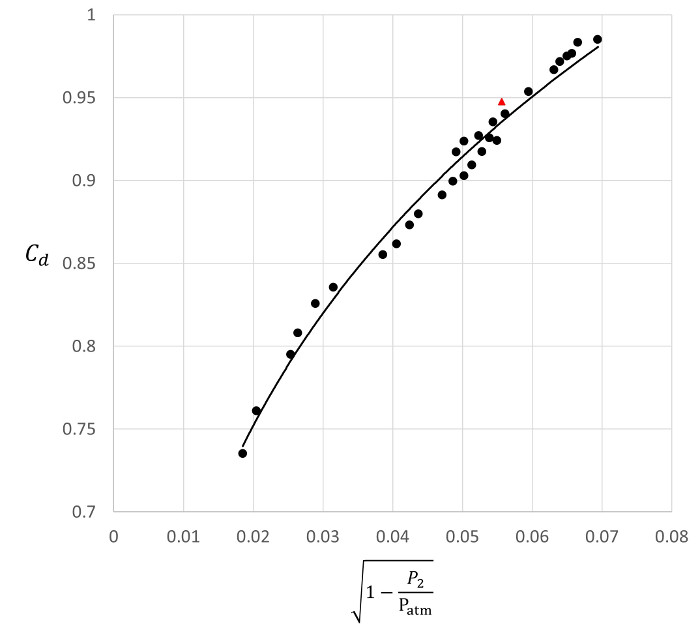
Figura 4. Resultados representativos.  : Coeficientes de descarga determinados em diferentes taxas de fluxo.
: Coeficientes de descarga determinados em diferentes taxas de fluxo.  : Coeficiente de descarga determinado com as medições de velocidade aqui demonstradas.
: Coeficiente de descarga determinado com as medições de velocidade aqui demonstradas.
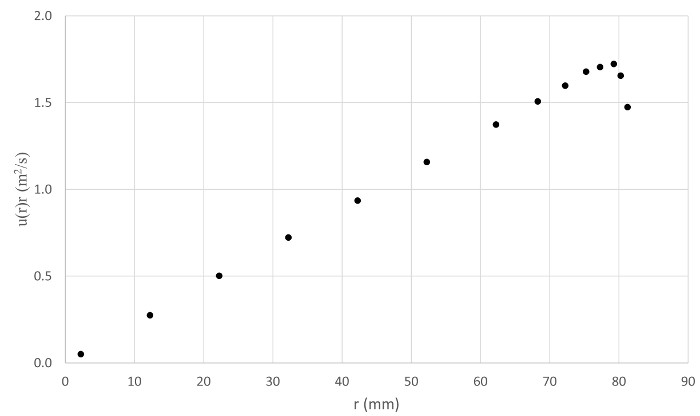
Figura 6. Resultados representativos. Enredo do produto entre velocidade e raio.
Mesa 3. Resultados representativos. Coeficiente de descarga.
| √(1-P2/Patm ) | Cd |
| 0.019 | 0.735 |
| 0.020 | 0.761 |
| 0.025 | 0.795 |
| 0.026 | 0.808 |
| 0.029 | 0.826 |
| 0.032 | 0.835 |
| 0.039 | 0.855 |
| 0.041 | 0.862 |
| 0.042 | 0.873 |
| 0.044 | 0.880 |
| 0.047 | 0.891 |
| 0.049 | 0.899 |
| 0.049 | 0.917 |
| 0.050 | 0.924 |
| 0.050 | 0.903 |
| 0.051 | 0.909 |
| 0.052 | 0.927 |
| 0.053 | 0.917 |
| 0.054 | 0.926 |
| 0.054 | 0.935 |
| 0.055 | 0.924 |
| 0.056 | 0.940 |
| 0.060 | 0.953 |
| 0.063 | 0.967 |
| 0.064 | 0.972 |
| 0.065 | 0.975 |
| 0.066 | 0.977 |
| 0.067 | 0.983 |
| 0.069 | 0.985 |
Aplicação e Resumo
Demonstramos a aplicação da análise de volume de controle da conservação da massa para calibrar uma passagem de fluxo como medidor de fluxo. Para isso, demonstramos o uso de um sistema pitot-estático para determinar a taxa de fluxo através da passagem de fluxo usando a integração sobre o perfil de velocidade. Em seguida, o conceito de coeficiente de descarga foi incorporado para explicar o efeito do crescimento da camada de fronteira perto das paredes da passagem de fluxo. Com base em um conjunto de medições de velocidade para diferentes taxas de fluxo, desenvolvemos uma regressão que expressa o coeficiente de descarga em função da razão entre a pressão estática na passagem de fluxo e a pressão atmosférica local,  . Finalmente, essa regressão foi incorporada em uma equação para a taxa de fluxo através da passagem em função de
. Finalmente, essa regressão foi incorporada em uma equação para a taxa de fluxo através da passagem em função de  . Esta equação foi desenvolvida para manter sua validade sob mudanças nas condições atmosféricas locais, tamanho da passagem e sistema unitário.
. Esta equação foi desenvolvida para manter sua validade sob mudanças nas condições atmosféricas locais, tamanho da passagem e sistema unitário.
A análise do volume de controle para conservação de massa oferece muitas alternativas para calibrar as passagens de fluxo como medidores de fluxo. Por exemplo, placas perfuradas, bicos e tubos venturi são usados em fluxos confinados para determinar a taxa de fluxo com base em alterações de pressão entre duas seções diferentes da passagem. E, assim como o nosso exemplo, esses dispositivos precisam ser caracterizados com um coeficiente de descarga que corrija os efeitos da camada de fronteira.
No fluxo por canais abertos, a análise de volume de controle para conservação de massa também pode ser usada para avaliar a taxa de fluxo, comparando a profundidade de fluxo antes e depois de restrições de fluxo, como vertedouros, portões parcialmente abertos ou reduções transversais. A principal importância dessas aplicações é que as estruturas hidráulicas para distribuição, controle e tratamento de água são de escalas muito grandes que impediriam o uso de outros dispositivos de fluxo.
Referências
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
- Chapra, S.C. and R.P. Canale. Numerical methods for engineers. Vol. 2. New York: McGraw-Hill, 1998.
- Buckingham, E. Note on contraction coefficients of jets of gas. Journal of Research, 6:765-775, 1931.
- Lienhard V, J.H. and J.H. Lienhard IV. Velocity coefficients for free jets from sharp-edged orifices. ASME Journal of Fluids Engineering, 106:13-17, 1984.
Pular para...
Vídeos desta coleção:

Now Playing
Conservação de Massa e Medições de Taxa de Fluxo
Mechanical Engineering
22.6K Visualizações

Empuxo e Arrasto em Corpos Imersos
Mechanical Engineering
29.9K Visualizações

Estabilidade de Embarcações Flutuantes
Mechanical Engineering
22.4K Visualizações

Propulsão e Impulso
Mechanical Engineering
21.6K Visualizações

Redes de tubulação e perdas de pressão
Mechanical Engineering
58.0K Visualizações

Resfriamento e Ebulição
Mechanical Engineering
7.7K Visualizações

Saltos Hidráulicos
Mechanical Engineering
40.9K Visualizações

Análise de Trocadores de Calor
Mechanical Engineering
28.0K Visualizações

Introdução à Refrigeração
Mechanical Engineering
24.6K Visualizações

Anemometria com fio quente
Mechanical Engineering
15.5K Visualizações

Medindo fluxos turbulentos
Mechanical Engineering
13.5K Visualizações

Visualização do Fluxo ao Redor de um Corpo Parado
Mechanical Engineering
11.8K Visualizações

Jato Incidindo em uma Placa Inclinada
Mechanical Engineering
10.7K Visualizações

Abordagem de Conservação de Energia para Análise de Sistemas
Mechanical Engineering
7.4K Visualizações

Determinação das Forças de Impacto em uma Placa Plana com o Método do Volume de Controle
Mechanical Engineering
26.0K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados