エントロピー

ソース:ミッチェル ・ ウィン博士は Ketron、 Asantha Cooray、PhD、物理教室 & 天文学、物理的な科学の学校、カリフォルニア大学、アーバイン、カリフォルニア州

熱力学第二法則は自然の基本法則です。それはシステムのエントロピーは常に時間の経過と共に増加またはシステムが定常状態または受けて、「元に戻せる状態プロセス」ときの理想的な例で一定している残る状態します。システムが不可逆過程中の場合システムのエントロピーは常に増加します。これは、ΔS、エントロピーの変化が常にゼロ以上であることを意味します。システムのエントロピーは、システムを得ることができる顕微鏡の構成の数の尺度です。たとえば、知られているボリューム、圧力、温度と容器内のガスは、個々 のガスの分子の構成の膨大な数を持つことができます。コンテナーが開いている場合は、ガス分子をエスケープし、本質的に無限に近づいて構成の数は大幅に増加します。コンテナーを開くと、エントロピーは増加します。したがって、エントロピーはシステムの「障害」の測定を考慮することができます。

エントロピーは、システムの現在の状態にだけ依存する量である「状態プロパティ」です。状態プロパティは、数量は、システムの現在の状態に到着パスに依存しません。したがって、state プロパティを定量化する最も便利な方法は、その変更を測定するためです。

エントロピー Sの変化は、として定義されます。

ΔS = Q/T(関係式 1)

、Qシステムに供給される熱は、 Tはシステムの温度。熱力学においては、作業のように、熱はエネルギーの伝達として定義されます。熱は、温度の相違のため、別の 1 つのオブジェクトから転送エネルギーです。氷と 0 ° C での水のお風呂をご検討ください。1 つが氷水風呂に熱供給、いくつかの氷が溶けるし、水の分子に利用可能な状態がシステムに追加された熱の量に比例して大量に増えます。エントロピーがこの金額に比例して増やしてください。異なる温度で 2 つのオブジェクト間の関係は最初にニュートンが説明。

ニュートンの冷却の法則のいくつかの物体の温度の変化の割合は独自の温度とその周辺の温度の差に比例した状態します。温度Tが温度T の_f、この時間の関数としての温度変化で閉じたシステムに配置されるオブジェクトのtは微分方程式で記述されます。

dT/dt = k (T T_f )、 (式 2)

、kオブジェクトとその周辺の特性に依存する定数です。1 方程式は 適宜 同等:

-k dt dT =/(T T_f ).(式 3)

両側の統合を与えます。

-k t = ログ (T T_f ) C. ログイン +(関係式 4)

方程式の両側に指数関数を適用し、再編成を与えます。

T T_f = C e^-kt 。(式 5)

時に初期温度T_は私は、問題のオブジェクト場合t = 0。

T は_私- T_f = c.(関係式 6)

それは時間の関数としての温度があること続きます。

T(t) = T_f + T_私- T_f e^-kt 。(関係式 7)

したがって、クーラーのクローズド システムのホット オブジェクトを配置すると、その温度は指数関数的速度で減少します。このクローズド システムでホット オブジェクトのQからの熱はクーラー周辺の温度を増加し、こうして使用可能な状態の数を増やします。したがって、ΔSエントロピーの変化は正とゼロ以外。

1. セットアップ。

1. 発熱体とスタンド、温度計、ストップウォッチ、いくつかの紙タオル、水、大きなビーカーを取得します。
2. サンプルがあまりにも急速にクールダウンしないように十分な水でビーカーを埋める (すなわち、少なくとも 500 mL)。
3. 加熱要素の下のスタンドに水のビーカーを置き、それをオンにします。
4. ビーカーの水の沸騰に達すると、温度計を挿入し、加熱要素をオフにします。
5. 慎重に加熱スタンドからビーカーを取り外します、ペーパー タオルの上に、テーブルの上に置きます。これらは、テーブルからの絶縁材として機能します。

2. 録音データ。

1. ストップウォッチを開始し、温度と時間を記録します。
2. 最初の 20 分間、1 分毎の測定を取る。
3. 次の 20 分、3-5 分毎の測定を取る。
4. 表 1にこれらの値を記録します。
5. .の時間と温度のグラフで表 1に収集されたデータ ポイントをプロットします。
6. K.冷却の一定の方程式 7を解決水と任意の 2 つのデータ ポイントの初期温度を使用すると、時間と温度を
7. K、プロット式 7 tの連続関数としてこの値を使用します。収集されたデータ ポイントを持つ関数を比較します。

680 mL 水の代表的な結果は表 1のとおりです。テーブル内のデータ ポイントを使用して解く方程式 7冷却定数kが発見されました。T(35) 35 分後 50.6 を =。初期温度は 100 ° C、およびデータ収集の 28.5 ° C で停止K:を取得する次の式は、これらの変数を使用して

50.6 = 28.5 + (100-28.5) e^{35 k}。(関係式 8)

K値kを与える解決 = 0.034。この冷却の定数のカーブが実験のデータ ポイントと共に図 1の灰色の破線として表示されます。式 6の機能のフォームでは、実験の結果を非常に密接に一致します。

水が冷えると、水の分子の減少を利用可能な状態の数はエントロピーが低下します。部屋の周囲の空気のエントロピー増加水ビーカー; それを囲む空気の分子に熱を移すため水の全体のエントロピー システムの増加の空気 +。今熱い空気の分子が占めることができる状態の数は、お湯が部屋に導入される前に、よりもはるかに高いです。

差動形態で熱 dQを追加または水から削除は、質量、比熱c間の関係を使用して計算でき、温度を変更します。

dQ = mc dT、 (式 9)

cは水の 4.18 J/(gK) で知られています。水のエントロピーの変化はします。

ΔS_水=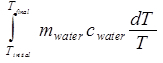

= m_水 c_水ln (T最終/T_初期)。(関係式 10)

K ケルビンへの変換を使用して ° C = + 273.15、水のエントロピーの変化として計算されます。

ΔS_水= 680 g * 4.18 J/(g K) * ln [(28.5 + 273.15)/(100 + 273.15)]

=-604 J/K.

等温プロセスですので、周囲の空気の温度は 20.4 ° C で一定です。空気のエントロピー変化はします。

ΔS_空気= 、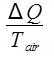

Qは方程式 9によって与えられる水によって放出される熱です。空気のエントロピーの変化は、としてを計算されます。

ΔS_空気=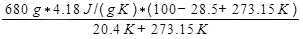

= 3337 J/K.

水と空気のエントロピーの変化量システム、ΔS の_トット水と大気のエントロピーの個々 の変更の合計であります。

ΔS の_トット= ΔS_水+ ΔS_空気 (式 11)

=-604 J/k + 3337 J/K

= 2733 J/K.

表 1。実験中の気温を記録しました。

時間 (分)	水の温度 (° C)
0 0	99.6
1 10	97.1
1 50	94.2
2 30	91.8
3 22	89
4 05	87.2
5 08	82.7
6 05	82.4
8 25	78
9 15	76.5
10 15	74.6
11 38	72.7
12 58	70.7
13 58	69.2
15 15	67.7
16 55	65.8
18 38	64
20 25	62.3
24 02	58.8
25 45	57.3
34 45	50.6
40 50	47.4
44 30	45.9
49 59	43.6
53 42	42.4
60 01	40.2
64 20	39.5
76 37	37
103 50	32.1
116 41	30.3
122 46	29.6
134 11	28.5

図 1.温度対時間のプロットします。ブルーのドットは実験データを示し、点線はニュートンの冷却の法則に基づく理論的なデータ。

袋に常に保ったヘッドフォンのペアがなる傾向があります結び目これは周りのバッグを運ぶによるエントロピーの増加。それら国連結び目にヘッドフォンで動作し (このことができると考えることの「可逆過程」) エントロピーを減少させる必要があります。物理的な法律によって許可される最も効率的な熱エンジン サイクルはカルノー サイクルです。2 番目の法則は、作業を行うすべての熱熱エンジンに供給されるが使えます。Carnot の効率は、使用できる熱の割合の制限の値を設定します。サイクルは、2 つの断熱プロセスに続いて 2 つの等温プロセスで構成されています。第二法則の古典的な例のヒートポンプだけで本質的にある冷蔵庫は。冷蔵庫は、熱を低温 (「ソース」) の 1 つの場所から機械的な仕事を使用してより高い温度 (「ヒートシンク」) で別の場所に移動します。第二法則によれば熱自発的にも流れていない寒い場所から熱い一;したがって、仕事 (エネルギー) は、冷凍の必要です。

ニュートンの冷却の法則は、100 ° c の水-空気系のエントロピーの増加につながった部屋の温度に冷却水のビーカーによって示されました。135 分の期間にわたって時間の関数としての水の温度を測定することにより、水の冷却が指数形式でことを確認することが可能だった。試料水の冷却の定数は、収集したデータを使用して冷却の方程式を解くことによって発見されました。