複数の方向のベクトル

ソース: ニコラス ・ ティモンズ、Asantha Cooray、PhD、物理学科 & 天文学、物理的な科学の学校、カリフォルニア大学、アーバイン、カリフォルニア州

この実験は、ベクトルを追加し、複数の方向を減算する方法を示しています。加算または減算の複数のベクトルの解析的計算する目標になり、実験、計算を確認します。

ベクトルとは、大きさと方向を持つオブジェクトです。ベクトルの大きさは、方向、 x軸と角度によって定義されます通常単に長さとして示されます。力はベクトルであるので、彼らはベクトルの物理的な表現として使用できます。力のシステムを設定して追加力勢力間の均衡が作成されますを見つけることにより、ベクトルのシステムは実験的検証できます。

図 1ベクトルを示しています、 x 軸とy軸との角度 θ を x軸となります。

図 1.

追加する 2 つのベクトルを減算するには、そのx 軸とy 軸の成分ベクトルを記述することをお勧めします。X成分として数学的に表されるx 軸方向で指すベクトルの量であります。

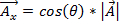.(関係式 1)

Y成分を表します。

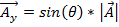.(式 2)

大きさが定義されています。

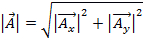.(式 3)

追加する 2 つのベクトルを減算するには、単にベクトルのxおよびyコンポーネントに分割、追加または減算、それぞれ対応するコンポーネント。

たとえば場合、ベクター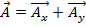とベクトル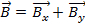、2 つのベクトルの付加、 。

ベクトルは、 x軸に対して角度 θ を決定するには、次の式を使用します。

.(関係式 4)

ベクトルには大きさと方向の両方があるため 2 つのベクトルを乗算することは 2 つの数値を乗算することと同じくらい簡単ではありません。ベクトルを乗算する 2 つの方法があります: 内積と外積。内積として書き込むことができます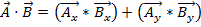または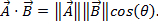ここで、θ は、2 つのベクトルの間の角度。結果のみ、大きさと方向ではないがあります。物理学で内積の応用は仕事 (W)、仕事が距離倍力として定義されている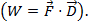として 2 つのベクターのクロス積を書き込むことができます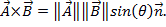クロス積に用語が含まれて間積と同様に、 、2 つのベクトルに垂直な大きさ 1 のベクトルとして定義されている、 。クロス積の結果はベクトルに。物理学でクロス積の 1 つの例はトルク、半径を倍力の結果であります。

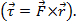
ベクトルは、重力や摩擦などの力をベクトルとして表すことができるので物理学で役立ちます。この演習では、重力の力を使用して、ベクターの性質の力、それらの力が複数の方向に追加する方法をデモンストレーションします。地球の表面の重力の力は、次のように、

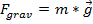、 (式 5)

どこ、物体の質量は、中は、重力加速度 (9.8 m/s²) 地球の表面の近く。

1. バランスを強制します。

1. 力表正反対の方向 (180 ° の角度の相違) に直面している同じ質量を持つ 2 つのプーリーを設定します。
2. それぞれの力に等しくなります。移動しないでください力の表の中央にリングを調べることによって、2 つの力が等しく、反対かどうかを確認します。
3. これらの力に関連付けられているベクトルのコンポーネントを追加する場合、結果として生じるベクトルがゼロの大きさを持っている注意してください。これは、すべての力は、平衡を決定する方法です。

2. 分析の計算。

1. この演習は、平衡の 3 つの力で構成されます。2 つの力を知られるが、3 番目が見つけた最初解析的ベクトル理論を用いたし、実験。この実習では、維持期間の 0 °。
2. されている場合とが知られていると均衡でその後は強制的に 2 つの原因、システムに追加されたとき、の合計に反対の方向では、大きさが等しくの ( + )。
3. 大きさを計算する、 。実際に使用するの単位である 1 ニュートン (N) と等しい力の。
4. どのような大きさの計算、ベクトルの理論を用いた合計だったかどうかになる ( + )。
5. どのような角度の計算、ベクトルの理論を用いた合計だったかどうかになる ( + )。

3. 実験。

1. テーブル 1の最初の行に次の値と、力のテーブルに 2 つの力を設定。維持してください0 °。
2. 第三勢力を設定、重みを加えると平衡に達するまで角度を変えることによって。表 2にこれらの値を記録します。
3. それぞれの 4 つの場合 3.2 の手順を繰り返します。
4. 計算による解析結果からの差の割合を決定、 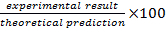。これらの計算値を表 2を完了します。

演習の結果は、表 1および表 2のとおりです。

表 1。セットアップ。

# を設定します。	A		B
	質量	角度	質量	角度
1	100	0	100	20
2	100	0	150	40
3	200	0	150	60
4	200	0	250	80

表 2。解析結果。

# を設定します。	大きさ (N)	大きさ (N)	角度 (°)	大きさ (N)	角度 (°)
1	0.98	0.98	20	1.93	10
2	0.98	1.47	40	2.31	24
3	1.96	1.47	60	2.98	25
4	1.96	2.45	80	3.39	45

表 3。実験結果。

# を設定します。	実験の規模 (N)	分析の大きさ (N)	違い (%)	実験的角度 (°)	分析の角度 (°)	違い (%)
1	2.1	1.93	9	11	10	10
2	2.2	2.31	5	26	24	8
3	2.8	2.98	6	28	25	12
4	3.5	3.39	3	43	45	5

実験の結果は、分析の計算と一致しています。2 つのベクトルの間の角度の合計は、 1-5 の方程式を使用して計算できます。方程式、力などの物理的なベクトルの計算を行うために有効です。

野球で外野手は、移動中のボールをキャッチするためにベクトルを理解するが。外野手には、ボールのスピードだけ知っていたなら、彼を右の代わりにレフトに実行し、ボールを見逃す可能性があります。彼はのみヒットの方向を知っていたなら、彼の頭の上帆ボールを見るためだけで充電可能性があります。彼はベクトルを理解し、ボールをヒットすると、すぐに彼考慮できる大きさと方向の両方彼が捕獲物を作るときに、ボールのどこを推定するために。

飛行機が空の場合、そのスピードと方向はベクトルとして記述できます。重い風、風ベクトルが結果システムのベクトルを与えるため平面のベクトルに追加します。たとえば場合、飛行機は風に、結果のベクトルの大きさなります初期の大きさより小さい。これは、直感的な理にかなっている風に向かうとき遅く動いて面に対応します。

2 つのオブジェクトが衝突する、一緒に固執する彼らの最終的な運動量 (ベクトル) は 2 つの初期運動量ベクトルの和として近似できます。これは現実の世界のように、簡素化、2 つのオブジェクトが衝突熱や衝突による変形のような考慮するべき余分な要因。勢いは、その速度を掛けたオブジェクトの質量だけです。別の方向に異なる速度で旅行氷の上二人のスケーターが衝突、互いに保持彼らの最終的な方向と速度を推定できる場合、初期ベクターのコンポーネントに基づいて。

この実験では、軍のベクターの性質は検討、測定されました。ベクトルが一緒に追加された、解析的および実験的に合力の大きさと方向が決定しました。