L'approche de la conservation de l'énergie pour l'analyse des systèmes
Vue d'ensemble
Source : Ricardo Mejia-Alvarez et Hussam Hikmat Jabbar, département de génie mécanique, Michigan State University, East Lansing, MI
Cette expérience vise à démontrer l’application de l’équation de conservation de l’énergie pour déterminer la performance d’un système de flux. À cette fin, l’équation de l’énergie pour l’écoulement régulier et incompressible est appliquée à un tuyau court muni d’un robinet-vanne. La vanne est fermée puis progressivement et son influence sur les conditions d’écoulement est caractérisée. En outre, l’interaction entre ce système d’écoulement et le ventilateur qui pousse le flux est étudiée en comparant la courbe du système avec la courbe caractéristique du ventilateur.
Cette expérience permet de comprendre comment la dissipation d’énergie est utilisée par vannes pour restreindre le flux. En outre, en vertu du même principe, cette expérience offre une méthode simple pour mesurer le débit en utilisant le changement de pression à travers une entrée nette.
Principles
Analyse du débit des fluides est fréquemment réalisée selon comment l’énergie se transforme comme le liquide s’écoule à travers un système. L’énergie totale transportée par un flux inclut l’énergie cinétique, potentielle et thermodynamique. Ces formes d’énergie peuvent se transformer librement les uns les autres, et l’énergie contenue dans le flux à une position donnée dans un système d’écoulement est l’équilibre entre l’énergie entrante totale, l’énergie supplémentaire et l’énergie soustraite. Ce bilan énergétique peut être exprimée sous forme d’équation comme suit [1, 2] :
 (1)
(1)
Ici, les sous-indices 1 et 5 se réfèrent aux conditions d’entrée et de sortie du système flux respectivement. Figure 2 (a) montre une représentation schématique du système flux : l’air passe par un flux conditionnement système, ou la contraction, appelé le plénum (sa décharge illustré à la Figure 3.a. Puis, il effectue une transition vers un court tuyau muni d’une soupape à son extrémité (voir Figure 2 b pour les détails de la tube/valve et les Figures 2 a et B pour les photos). Les rejets de l’air de la valve dans un espace clos, isolé de l’extérieur appelé « récepteur » (pour référence, voir Figure 3). Comme illustré à la Figure 3, le récepteur est suffisamment grand pour accueillir le système d’acquisition de données et les expérimentateurs. Enfin, l’écoulement s’arrête le récepteur à travers une tôle perforée qui agit comme un amortisseur pour la régulation du débit (voir Figure 3 c pour référence). L’air est ensuite capturé par un ventilateur centrifuge qui évacue vers l’atmosphère. Les termes entre parenthèses représentent le contenu d’énergie spécifique à chaque port, qui est la somme de l’énergie gravitationnelle de potentiel  , l’énergie cinétique
, l’énergie cinétique 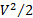 et thermodynamiques (ou potentiel de pression) énergie
et thermodynamiques (ou potentiel de pression) énergie  . Le coefficient de
. Le coefficient de  est utilisé pour prendre en compte la forme du profil de la vitesse. Pour l’instant expérimenter
est utilisé pour prendre en compte la forme du profil de la vitesse. Pour l’instant expérimenter 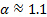 parce que l’écoulement est turbulent [1, 2]. Par conséquent, le côté gauche de l’équation (1) représente le changement de contenu énergétique entre les ports d’entrée et de sortie. En l’absence de travail externe ou effets dissipatifs, cette différence est égale à zéro. Cependant, la plupart des applications techniques portant sur les flux réels incluent addition ou soustraction d’énergie au moyen de machines de débit,
parce que l’écoulement est turbulent [1, 2]. Par conséquent, le côté gauche de l’équation (1) représente le changement de contenu énergétique entre les ports d’entrée et de sortie. En l’absence de travail externe ou effets dissipatifs, cette différence est égale à zéro. Cependant, la plupart des applications techniques portant sur les flux réels incluent addition ou soustraction d’énergie au moyen de machines de débit, et les effets dissipatifs,
et les effets dissipatifs, . Ces deux effets sont inclus sur la partie droite de l’équation (1).
. Ces deux effets sont inclus sur la partie droite de l’équation (1).
Dans cette expérience, un ventilateur centrifuge sera utilisé pour induire l’écoulement, c'est-à-dire, d’ajouter l’énergie au fluide. Pour ce genre de machine, le terme  est une fonction du débit
est une fonction du débit  appelée courbe caractéristique et est déterminée expérimentalement :
appelée courbe caractéristique et est déterminée expérimentalement :
 (2)
(2)
Ici, 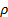 et
et  sont la densité et la viscosité cinématique de l’air à des conditions locales, et
sont la densité et la viscosité cinématique de l’air à des conditions locales, et 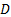 est le diamètre du système flux (
est le diamètre du système flux ( mm en la présente expérience). L’équation (2) est dans une forme qui fait en sorte que l’une des constantes dans le premier et le second terme sont sans dimension, alors que la constante dans la troisième partie est en unités de pression (Pa) pour garantir l’homogénéité dimensionnelle. L’équation (2) est la « courbe de performance de Fan » illustrée à la Figure 1.
mm en la présente expérience). L’équation (2) est dans une forme qui fait en sorte que l’une des constantes dans le premier et le second terme sont sans dimension, alors que la constante dans la troisième partie est en unités de pression (Pa) pour garantir l’homogénéité dimensionnelle. L’équation (2) est la « courbe de performance de Fan » illustrée à la Figure 1.
Enfin, la dissipation de l’énergie est proportionnelle à l’énergie cinétique de l’écoulement :
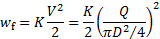 (3)
(3)
Notez que, en utilisant l’équation de continuité ( , où
, où 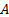 est la section transversale [1, 2]), la dissipation de l’énergie peut aussi être écrit en ce qui concerne le débit,
est la section transversale [1, 2]), la dissipation de l’énergie peut aussi être écrit en ce qui concerne le débit, . La figure 1 présente cette dernière forme de l’équation (3) comme la « courbe de système d’écoulement ». Dans l’équation (3), le coefficient de proportionnalité
. La figure 1 présente cette dernière forme de l’équation (3) comme la « courbe de système d’écoulement ». Dans l’équation (3), le coefficient de proportionnalité  , s’appelle le coefficient de perte et est l’addition de tous les effets dissipatifs induites par les éléments du système de circulation à la suite des interactions visqueux. Tandis que les contributions des tuyaux et conduits dépendent de leur rugosité, longueur et nombre de Reynolds, la contribution de raccords de tuyauterie, entrées et rejets, expansions, contractions, coudes et soupapes dépend de leurs géométries particulières. Pour l’instant, expérimenter, le coefficient de perte globale est la combinaison d’une entrée et une soupape de décharge :
, s’appelle le coefficient de perte et est l’addition de tous les effets dissipatifs induites par les éléments du système de circulation à la suite des interactions visqueux. Tandis que les contributions des tuyaux et conduits dépendent de leur rugosité, longueur et nombre de Reynolds, la contribution de raccords de tuyauterie, entrées et rejets, expansions, contractions, coudes et soupapes dépend de leurs géométries particulières. Pour l’instant, expérimenter, le coefficient de perte globale est la combinaison d’une entrée et une soupape de décharge :
 (4)
(4)
Où les valeurs des coefficients de perte d’entrée et d’évacuation sont 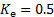 et
et  respectivement (voir [1, 2] pour référence). Le coefficient de perte de la vanne,
respectivement (voir [1, 2] pour référence). Le coefficient de perte de la vanne,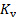 , nous le verrons dans la section suivante.
, nous le verrons dans la section suivante.
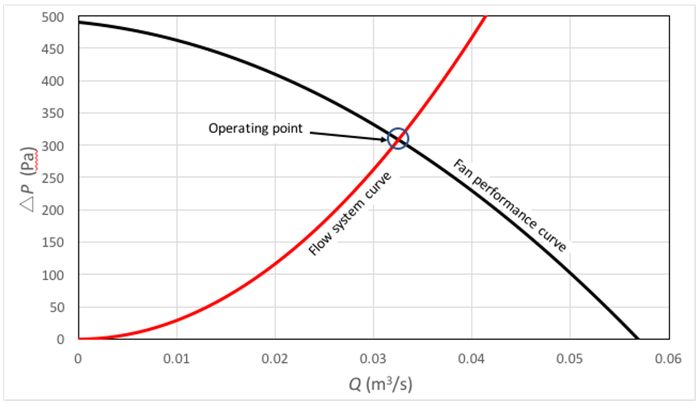
Figure 1. Exemple de courbe de système et de la courbe de performances de ventilateur.  : courbe système ;
: courbe système ;  : courbe de performances de ventilateur. Le cercle bleu met en évidence l’intersection entre les deux courbes, qui est le point de fonctionnement.
: courbe de performances de ventilateur. Le cercle bleu met en évidence l’intersection entre les deux courbes, qui est le point de fonctionnement.

Figure 2. Paramètre expérimental. (A) : écoulement facilité. Le flux se déplace de de gauche à droite ; il pénètre dans la chambre de tranquillisation via un flux de section, de conditionnement puis coule dans le tuyau et la vanne, les rejets à l’intérieur du récepteur et quitte enfin le système par le ventilateur. (B) : détails de l’équipement d’acquisition flux système et vos données. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Figure 3. Système d’acquisition de données. (A) les connexions de ces matériels d’acquisition de données suivent le schéma de la Figure 2 b. (B) virtual interface d’acquisition de données (écrite en LabView). S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.
Caractéristiques de la dissipation d’une vanne
Étant donné que les vannes sont essentiellement des dispositifs de la géométrie variable, leur coefficient de perte est fonction de l’angle de rotation de leur arbre ( ). Dans cette optique,
). Dans cette optique,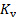 varie comme la vanne est ouverte ou fermée selon la relation suivante :
varie comme la vanne est ouverte ou fermée selon la relation suivante :
 (5)
(5)
Ici, nous avons utilisé l’équation de continuité à nouveau exprimer le coefficient de perte en fonction de la vitesse d’écoulement. Par ailleurs, l’équation (5) suggère que nous pouvons déterminer le coefficient de perte de la vanne en connaissant la valeur de la vitesse d’écoulement et la chute de pression à travers la vanne en fonction de l’ouverture angle et le débit : . C’est aussi la différence de pression entre les points 3 et 4 de la Figure 2 b (
. C’est aussi la différence de pression entre les points 3 et 4 de la Figure 2 b ( ).
).
Point de fonctionnement
Comme illustré à la Figure 1, le Point de fonctionnement d’un système de flux entraîné par une machine de flux, comme celui présenté dans cette expérience, est donnée par le point d’intersection de la courbe caractéristique du ventilateur et la courbe débit-système. Ce point peut être caractérisé en utilisant l’équation de l’énergie comme suit : comme peut être vu dans la Figure 2 a, l’air entre dans le système d’écoulement d’une grande salle aux conditions atmosphériques et aux sorties à la même pièce sans changement significatif en hauteur. En conséquence, pression, vitesse et la hauteur des conditions à l’entrée et la sortie du système (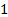 et
et  sous-indices dans l’équation (1) respectivement) sont identiques et s’annulent mutuellement. Par conséquent, l’énergie ajoutée par le ventilateur est compensée par l’énergie dissipée par le système d’écoulement. En d’autres termes, les équations (2) et (3) forment une égalité qui se traduit par la relation suivante, après simplification :
sous-indices dans l’équation (1) respectivement) sont identiques et s’annulent mutuellement. Par conséquent, l’énergie ajoutée par le ventilateur est compensée par l’énergie dissipée par le système d’écoulement. En d’autres termes, les équations (2) et (3) forment une égalité qui se traduit par la relation suivante, après simplification :
 (6)
(6)
La racine positive de cette équation exprime le Point de fonctionnement :
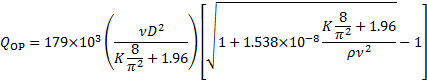 (7)
(7)
Ici, le sous-indice « OP » signifie « Point de fonctionnement ». Le coefficient de perte dans l’équation (7) est l’addition des coefficients de perte de l’entrée et soupape de décharge. Des équations (4) et (5) :
 (8)
(8)
Mesure du débit
Analogue à toutes les analyses précédentes, l’équation (1) est appliquée entre le plenum et un point en aval de l’entrée nette (points 2 et 3 de la figure 2 b à récupérer l’équation suivante :
 (9)
(9)
Ici, nous avons utilisé le fait qu’il n’y a aucun changement de hauteur entre les points 2 et 3, et la vitesse à l’intérieur de l’Assemblée plénière est négligeable. Présentation de l’équation de continuité (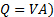 et l’équation (3), nous arrivons à la relation suivante pour le débit en fonction de la différence de pression entre le plenum (point 2 de la Figure 2 b et la pression statique en amont de la vanne (le point 3 à la Figure 2 (B)) :
et l’équation (3), nous arrivons à la relation suivante pour le débit en fonction de la différence de pression entre le plenum (point 2 de la Figure 2 b et la pression statique en amont de la vanne (le point 3 à la Figure 2 (B)) :
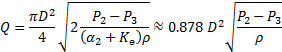 (10)
(10)
La constante 0,878 est obtenue après son remplacement pour les valeurs de la correction de vitesse et le coefficient de perte (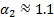 et
et 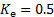 , voir [1, 2] par référence) et le regroupement de toutes les constantes dans un seul.
, voir [1, 2] par référence) et le regroupement de toutes les constantes dans un seul.
Procédure
1. réglage de l’installation
- Assurez-vous que le ventilateur ne tourne pas, donc il n’y a pas de débit dans l’installation.
- Vérifiez que le système d’acquisition de données (Figure 4(A)) suit le schéma figure 2 b.
- Connectez le port positif du transducteur de pression #1 (voir la figure 2 b pour la référence) à la prise de pression en amont de la vanne (
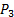 ).
). - Quitter le port négatif du transducteur de pression #1 ouvert aux conditions salle (récepteur :
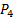 ). Par conséquent, la lecture de ce capteur sera directement
). Par conséquent, la lecture de ce capteur sera directement  .
. - Connectez le port positif du transducteur de pression #2 (voir la figure 2 b pour la référence) à la prise de pression du plénum (
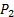 ).
). - Connectez le port négatif du transducteur de pression #2 (voir la figure 2 b pour la référence) à la prise de pression en amont de la vanne (
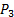 ). Par conséquent, la lecture de ce capteur sera directement
). Par conséquent, la lecture de ce capteur sera directement , tel que requis par l’équation (10).
, tel que requis par l’équation (10).
- Connectez le port positif du transducteur de pression #1 (voir la figure 2 b pour la référence) à la prise de pression en amont de la vanne (
- Assurez-vous que le canal virtuel 0 dans le système d’acquisition de données (Figure 4B) correspond au capteur de pression #1 (
 ) et le canal virtuel 1 correspond au capteur de pression #2 (
) et le canal virtuel 1 correspond au capteur de pression #2 ( ).
). - Définir le système d’acquisition de données de l’échantillon à une fréquence de 100 Hz pour un total de 500 échantillons (c'est-à-dire 5 s des données).
Le tableau 1. Paramètres de base pour l’étude expérimentale.
|
Paramètre |
Valeur |
| Diamètre du tuyau (D) | 50,8 mm (2 pouces) |
| Constante de calibration transducteur #1 (m_p1) |
|
| Constante de calibration transducteur #2 (m_p2) |
|
| Pression atmosphérique locale | 100,474.15 Pa |
| Température locale | 297.15 K |
| Densité de l’air local | 1,186 kg/m3 |

Figure 4 . Facilité de circulation. (A) : vue du plénum Ilestinterditderejeterà la section récepteur avant d’installer le jeu des soupapes à étudier. (B) : 3 types différents de vannes dans le récepteur. De gauche à droite : gate valve, vanne, vanne papillon. (C) : sortie des ports du récepteur. Les soupapes de décharge le flux à l’intérieur du récepteur, et le ventilateur aspire l’écoulement sur le récepteur à travers la tôle perforée dans l’image. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.
2. les mesures
- Enregistre le diamètre du tuyau relié à la vanne et on calcule son aire de section.
- Déterminer le nombre maximal de tours complets de la poignée pour soulever la soupape de la position complètement fermée à la position complètement ouverte. Si ce nombre n’est pas un entier, exclure la dernière rotation fractionnaire pour simplifier cette analyse. Pour l’expérience en cours, le nombre maximal de tours complets est 12.
- Fermer complètement la vanne.
- Tournez la poignée de la vanne jusqu'à ce qu’il est complètement ouvert, tout en comptant le nombre de tours complets. Pour plus de simplicité, utilisez uniquement un nombre entier de tours pour l’expérience. Par exemple, il faut environ 12 tours et 1/3 de tour pour ouvrir complètement la vanne utilisée dans cette expérience. Par conséquent, nous tourner la poignée de cette valve seulement 12 tours complets de sa position de fermeture complète et qui définissent comme la position initiale (
 ).
). - Allumez la facilité de circulation.
- Utilisez le système d’acquisition de données pour enregistrer les lectures de
 et
et  .
. - Entrez dans le tableau 2, les valeurs moyennes de
 et
et  obtenus avec le système d’acquisition de données.
obtenus avec le système d’acquisition de données. - Fermer la vanne 1,5 tour à tour.
- Répétez les étapes 2.6 à 2.8 jusqu'à ce que le tableau 2 est complètement rempli.
- Désactiver l’installation des flux.
3. analyse des données
- Déterminer le coefficient de perte de la vanne pour chaque position angulaire en utilisant l’équation (5). Entrez ces valeurs dans le tableau 2.
- Déterminer le débit pour chaque position angulaire de la soupape en utilisant l’équation (10). Entrez ces valeurs dans le tableau 2.
- Déterminer le point de fonctionnement à l’aide d’équation (7). Entrez ces valeurs dans le tableau 2.
- Calculer l’écart relatif entre le débit et le point de fonctionnement
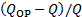
- Utiliser l’équation (3) pour produire un tracé des courbes de système pour toutes les valeurs de
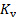 . Tenir compte du coefficient de perte totale comme
. Tenir compte du coefficient de perte totale comme  .
. - Ajouter la courbe caractéristique du ventilateur à cette même parcelle en utilisant l’équation (2).
Le tableau 2. Résultats représentatifs. Mesures de différence de pression et des estimations des coefficients de taux et de la perte de débit.
| [P_pl-P_a] (Pa) | [P_a-P_r] (Pa) | Q (m3/s) | K | Q_OP (m3/s) | Ε (%) |
| 246,75 | 54.00 | 0,0327 | 0,450 | 0.0316 | -3.16 |
| 208.62 | 114.22 | 0.0301 | 0,976 | 0.0293 | -2.51 |
| 156.19 | 204,80 | 0.0260 | 2.198 | 0,0254 | -2.30 |
| 109.30 | 281.69 | 0.0218 | 4.224 | 0.0214 | -1,53 |
| 71,82 | 348.38 | 0.0176 | 7.863 | 0,0174 | -1,26 |
| 38,72 | 408.60 | 0.0129 | 16.989 | 0.0128 | -0,90 |
| 15 h 00 | 452.39 | 0,0081 | 48.359 | 0,0080 | -0,32 |
| 2.51 | 482.50 | 0,0033 | 307.799 | 0,0033 | -0,18 |
Résultats
La figure 5 montre les résultats pour les mesures. Ici, la ligne noire épaisse a été générée avec l’équation (2) et chaque ligne rouge avec l’équation (3) pour différentes valeurs du coefficient de perte de la soupape. De la figure, il est évident que la courbe du système augmente sa pente lorsque la vanne se ferme. En d’autres termes, cette expérience montre que le principe qui sous-tend le fonctionnement d’une vanne est d’augmenter la dissipation de l’énergie afin de limiter le débit. En revanche, l’équation (5), on pouvait déduire que la valeur de 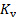 devient infini lorsque la vanne est fermée. D’un point de vue conceptuel, cette condition signifie que toute l’énergie est dissipée, donc complètement entraver des flux à travers la valve.
devient infini lorsque la vanne est fermée. D’un point de vue conceptuel, cette condition signifie que toute l’énergie est dissipée, donc complètement entraver des flux à travers la valve.
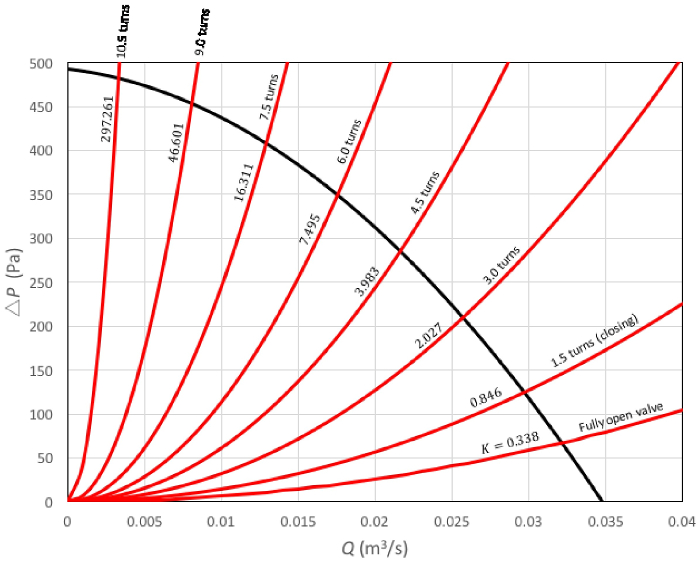
Figure 5 . Résultats représentatifs.  : courbes de système. Chaque courbe dans cette famille est le résultat d’un degré différent d’ouverture des soupapes. La pente de la courbe augmente à mesure que la vanne est fermée. Chaque courbe a son coefficient de perte correspondante pour référence ;
: courbes de système. Chaque courbe dans cette famille est le résultat d’un degré différent d’ouverture des soupapes. La pente de la courbe augmente à mesure que la vanne est fermée. Chaque courbe a son coefficient de perte correspondante pour référence ;  : courbe de performances de ventilateur. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.
: courbe de performances de ventilateur. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.
Comme indiqué dans le tableau 2, l’erreur entre le débit estimé au point d’utilisation (équation (7)) et le débit mesuré (équation (10)) reste inférieure à 3,2 % pour la gamme étudiée des débits. S’il s’agit d’un résultat satisfaisant étant donné le faible pourcentage d’erreur, le débit estimé au point de fonctionnement est toujours sous-estimée et suit une tendance décroissante comme la vanne se ferme progressivement. Cette tendance offre un aperçu du comportement du système flux, notamment parce que la valeur de la correction de facteur de vélocité non-uniformité augmente légèrement avec le nombre de Reynolds. Il n’est donc pas surprenant que l’erreur augmente avec la vitesse d’écoulement.
augmente légèrement avec le nombre de Reynolds. Il n’est donc pas surprenant que l’erreur augmente avec la vitesse d’écoulement.
Applications et Résumé
Cette expérience a exploré l’application de l’équation de l’énergie pour caractériser l’action d’une vanne sur le débit de la canalisation. Il a été observé que la valve induit la résistance à l’écoulement en augmentant la dissipation d’énergie. Considérant que la chute de pression le long du système de débit est directement proportionnelle au carré de la vitesse d’écoulement, l’effet de dissipation d’énergie est capturée par la grandeur du coefficient de proportionnalité. Ce coefficient est l’addition des coefficients de perte de tous les éléments dans le système de flux, y compris la vanne. Le coefficient de perte de la valve augmente de façon monotone comme la vanne se ferme progressivement. Et cet effet augmente la pente de la courbe de système ainsi, atteignant une valeur de l’infini quand la vanne est fermée.
Le comportement décrit ci-dessus a été contrasté avec la courbe de rendement du ventilateur centrifuge qui anime la circulation. En comparant le flux taux mesuré directement avec le débit estimé par l’intersection de la courbe de système et la courbe de rendement du ventilateur, il a été démontré que ce point d’intersection définit les conditions de fonctionnement de la demande de pression et des taux de débit.
Cette expérience a servi le but de démontrer les principes de conservation de l’énergie pour caractériser quelques différentes applications d’ingénierie : soupape de fonctionnement, mesure de débit des taux et conditions d’un système de flux d’exploitation. Conservation de l’énergie peut être utilisée essentiellement pour caractériser tout système d’écoulement, ce sont deux autres exemples d’applications de l’équation de l’énergie :
L’énergie cinétique, emporté par le vent peuvent être récoltée par des éoliennes pour produire l’énergie électrique. En comparant en amont avec des conditions d’écoulement en aval, l’équation de l’énergie permet d’évaluer la quantité d’énergie a été retiré de la vent. L’ampleur de l’énergie récupéré sera donnée par le travail de l’arbre, , dans l’équation (1).
, dans l’équation (1).
Changement des énergie potentielle gravitationnelle peut servir à évaluer la vitesse d’écoulement d’eau sur un déversoir. Ceci est fait en combinaison avec l’équation de conservation de masse en mesurant les profondeurs en amont et en aval du déversoir. Pour un écoulement turbulent, l’équation suivante serait une bonne approximation de la vitesse d’écoulement sur l’évacuateur de crues :
 (11)
(11)
Ici,  est la largeur de la chaîne et
est la largeur de la chaîne et  et
et  sont respectivement les profondeurs en amont et en aval.
sont respectivement les profondeurs en amont et en aval.
References
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
Tags
Passer à...
Vidéos de cette collection:

Now Playing
L'approche de la conservation de l'énergie pour l'analyse des systèmes
Mechanical Engineering
7.4K Vues

Flottabilité et traînée sur les corps immergés
Mechanical Engineering
29.9K Vues

Stabilité des vaisseaux flottants
Mechanical Engineering
22.4K Vues

Propulsion et poussée
Mechanical Engineering
21.6K Vues

Réseaux de canalisations et pertes de charge
Mechanical Engineering
58.0K Vues

Refroidissement et ébullition
Mechanical Engineering
7.7K Vues

Ressauts hydrauliques
Mechanical Engineering
40.9K Vues

Analyse des échangeurs de chaleur
Mechanical Engineering
28.0K Vues

Introduction à la réfrigération
Mechanical Engineering
24.6K Vues

Anémomètre à fil chaud
Mechanical Engineering
15.5K Vues

Mesure des écoulements turbulents
Mechanical Engineering
13.5K Vues

Visualisation de l'écoulement après un corps non profilé
Mechanical Engineering
11.8K Vues

Impact d'un jet sur un plan incliné
Mechanical Engineering
10.7K Vues

Conservation de la masse et mesures de débit
Mechanical Engineering
22.6K Vues

Détermination des forces d'impact sur une surface plane via la méthode des volumes de contrôle
Mechanical Engineering
26.0K Vues