Ley de Hooke y el movimiento armónico simple
Fuente: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Departamento de física & Astronomía, Facultad de ciencias física, Universidad de California, Irvine, CA
Energía potencial es un concepto importante en la física. Energía potencial es la energía asociada con las fuerzas que dependen de la posición de un objeto en relación con su entorno. Energía potencial gravitatoria, que se discute en otro video, es la energía asociada que es directamente proporcional a la altura de un objeto sobre la tierra. Asimismo, es posible definir la energía potencial del resorte, que es directamente proporcional al desplazamiento de un resorte de su estado de relajación. Un resorte estirado o comprimido tiene energía potencial, ya que tiene la capacidad de trabajar sobre un objeto. La capacidad de"trabajar" es a menudo citada como la definición fundamental de la energía.
Este video demuestra la energía potencial almacenada en los resortes. También verificará la restauración ecuación de fuerza de los resortes, o ley de Hooke. La constante del resorte es diferente para los resortes de diferentes elasticidades. Se verificará la ley de Hooke y la constante de resorte medida por diferentes pesos a un resorte suspendido y los desplazamientos resultantes de la medición.
Sostiene un resorte en cualquiera posición estirado o comprimido requiere que alguien o algo ejerce una fuerza sobre el resorte. Esta fuerza es directamente proporcional a la dislocación, Δy, de la primavera. A su vez, el resorte ejercerá una igual y opuesta fuerza:
F = -k Δy, (ecuación 1)
donde k se llama la "constante de rigidez del resorte". Esto se refiere a menudo como una "fuerza de restauración" porque el resorte ejerce una fuerza en dirección opuesta al desplazamiento, indicado por el signo negativo. Ecuación 1 se conoce como ley de Hooke.
Movimiento armónico simple se produce cuando existe una fuerza restauradora es proporcional al desplazamiento del equilibrio, como en la ley de Hooke. De la segunda ley de Newton, F = may reconociendo que la aceleración a es la segunda derivada del desplazamiento con respecto al tiempo, 1 de la ecuación puede ser reescrita como:
m (d2y/dt2) = y -k. (Ecuación 2)
La solución a este diferencial de segundo orden es bien conocida por ser:
y (t) = pecado (ωt + φ), (ecuación 3)
donde A es la amplitud de oscilación, ω = (k/m)1/2y la fase ángulo φ depende de las condiciones iniciales del sistema. Ecuaciones en la forma de la ecuación 3 describen lo que se denomina movimiento armónico simple. El período T, la frecuencia fy la constante ω están relacionados por:
Ω = 2πf = 2π/T. (ecuación 4)
Así, el período T está dado por:
T = 2π (m/k)1/2. (Ecuación 5)
Tenga en cuenta que T no depende de la amplitud A de la oscilación. Por lo tanto, si un peso se cuelga de un resorte suspendido de la vertical, el período resultante de la oscilación es proporcional a la raíz cuadrada del peso adjunto.
El trabajo requerido para estirar el resorte una distancia es W = <F> y, donde <F> es la fuerza promedio necesaria para estirar la cadena. Puesto que F es lineal en y, la media es a la fuerza en equilibrio (= 0) y la fuerza en y:
<F> = ½ [0 + ky]. (Ecuación 6)
El trabajo realizado y por lo tanto la energía potencial elástica, PE, se pueden escribir como:
PE = ½ k y2. (Ecuación 7)
En esta práctica se medirá la energía potencial de un resorte.
1. medir la constante elástica y la energía potencial de un resorte y confirmar la relación entre la masa y oscilatoria T. período
- Obtener un resorte con una constante de resorte conocido, un soporte para colocar el resorte, por lo menos 5 pesas de diferentes masas que pueden acoplarse a la primavera, un palo de metro y un cronómetro.
- Asegure el soporte de una base sólida y enganchar el resorte en el soporte. Asegúrese de que hay suficiente espacio debajo de la primavera para que estire sin golpear la mesa o el suelo.
- Cada una de las masas, calcular la fuerza ejercida sobre el muelle por la fuerza gravitacional de la tierra (F = mg). Comience con el peso menos masiva. Registrar estos valores en la tabla 1.
- Medir la primavera como muy por encima de la superficie de la mesa es en su posición sin estirado.
- El peso menos masiva a la primavera y medir el Δy1 de desplazamiento (ver figura 1). Grabar este desplazamiento en la tabla 1.
- Con el peso añadido, levante un poco el peso antes de soltarlo. Observar el movimiento oscilatorio. Medir el periodo T con un cronómetro. Para una medición más precisa, el tiempo durante múltiples períodos de registro y dividir ese tiempo por el número de períodos observados. No esta varias veces y registrar el promedio de tiempo medido para el período T en la tabla 1.
- Repita los pasos 1.5-1.6 para todas las masas, en orden creciente de masa.
- Calcular la energía potencial del resorte para cada una de las diferentes masas y regístrelos en la tabla 1.
- Parcela la fuerza F en función del desplazamiento Δy. Según la ecuación 1, este debe ser lineal. Montar una pista a la línea. Esta vertiente corresponde a primavera constante k. Compare el valor medido con el valor conocido de la primavera.
- La primavera conocida constante y la ecuación 5, calcular lo que debería ser el período T de oscilación para cada una de las masas; informan en la tabla 1. Compararlos con la T que se midió con un cronómetro en el paso 1.6.
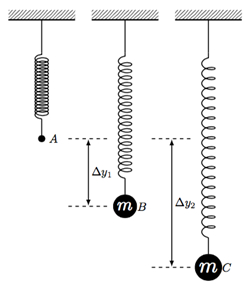
Figura 1: Oscilación del muelle,
Resultados representativos del experimento, llevado a cabo con un resorte de constante k = 10 N/m, se muestran en la tabla 1. La representación gráfica de F frente a la Δ de desplazamientoy se grafica a continuación en la figura 2. La función lineal se cabe con una línea y la pendiente de la recta es igual a la constante de resorte, dentro de un margen de error. La linealidad de los resultados demuestra la validez de la ley de Hooke (ecuación 1).
Revise la tabla 1 para ver cómo el período T de oscilación se relaciona con la masa que se une a la primavera. La más pesada la masa atada a la primavera, el período será, como es proporcional a la raíz cuadrada de la masa (ecuación 5). También, tenga en cuenta que cuando una masa más grande se adjunta al final de la primavera, la primavera se estirar aún más. La energía potencial del sistema es mayor, ya que es una función de los desplazamientos cuadrados de equilibrio (ecuación 7). Es lógico que el período es más largo para una masa más grande, porque la primavera es desplazada lejos de equilibrio, tarda más en recorrer esa distancia más.
Tabla 1. Resultados.
| Masa (kg) | Peso / F (N) | Δy (m) | PE (J) | T medido (s) | T calculado (s) |
| 0.5 | 4.9 | 0.49 | 2.4 | 1.3 | 1.4 |
| 0.75 | 7.4 | 0.74 | 5.4 | 1.6 | 1.7 |
| 1 | 9.8 | 0.98 | 9.6 | 1.9 | 1.9 |
| 1.5 | 14.7 | 1.5 | 21.6 | 2.5 | 2.4 |
| 2 | 19.6 | 2 | 38.4 | 2.9 | 2.8 |
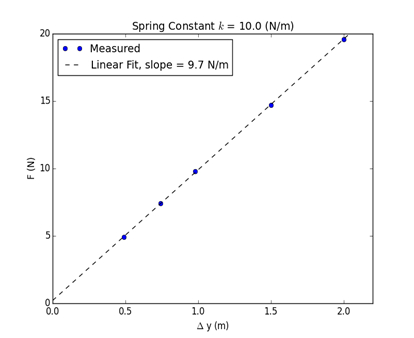
Figura 2: Diagrama de fuerza aplicada (N) versus desplazamiento.
El uso de resortes es omnipresente en nuestra vida cotidiana. La suspensión de los coches modernos está hecha de resortes que son bien amortiguados. Esto requiere el conocimiento de las constantes de resorte. Para los paseos más suaves de Cadillac, se utilizan resortes con una constante de resorte más baja, y el viaje es "mushier." Coches de alto rendimiento utilizan muelles con una constante de resorte más alta para un mejor manejo. Trampolines también se hacen con los resortes de constantes de resorte diferentes, dependiendo de cuánto se desea el "rebote" cuando buceo fuera del tablero. Cuerdas de escalada de roca son también ligeramente elásticos, así que si un escalador cae al subir, la cuerda no salvarla de golpear el suelo, sino también frenaría la caída con su elasticidad. El más pequeño la constante del resorte de una cuerda de escalada, más estrechamente se asemeja a puenting.
En este estudio, se midió el desplazamiento de un resorte resultante de la aplicación de fuerzas de diferentes magnitudes. La validez de la ley de Hooke se verificó mediante la representación de los desplazamientos resultantes en función de la fuerza ejercida sobre el resorte de suspensión. También se observó movimiento oscilatorio, con períodos de proporcionales a la raíz cuadrada de la masa atada a la primavera.
Saltar a...
Vídeos de esta colección:

Now Playing
Ley de Hooke y el movimiento armónico simple
Physics I
61.3K Vistas

Las leyes del movimiento de Newton
Physics I
75.7K Vistas

Fuerza y aceleración
Physics I
79.1K Vistas

Vectores en múltiples direcciones
Physics I
182.3K Vistas

Cinemática y movimiento de proyectiles
Physics I
72.6K Vistas

Ley de la gravitación Universal de Newton
Physics I
190.8K Vistas

Conservación del momento
Physics I
43.3K Vistas

Fricción
Physics I
52.9K Vistas

Diagramas de equilibrio y de cuerpo libre
Physics I
37.3K Vistas

Esfuerzo torsional
Physics I
24.3K Vistas

Inercia rotacional
Physics I
43.5K Vistas

Momento angular
Physics I
36.2K Vistas

Energía y trabajo
Physics I
49.7K Vistas

Entalpía
Physics I
60.4K Vistas

Entropía
Physics I
17.6K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados