Vectores en múltiples direcciones
Fuente: Nicolás Timmons, Asantha Cooray, PhD, Departamento de física de & Astronomía, Facultad de ciencias física, Universidad de California, Irvine, CA
Este experimento demuestra cómo vectores suma y restan en múltiples direcciones. El objetivo será calcular analíticamente la suma o resta de vectores múltiples y luego confirmar experimentalmente los cálculos.
Un vector es un objeto con magnitud y dirección. La magnitud de un vector se denota simplemente como la longitud, mientras que la dirección es normalmente definida por el ángulo que hace con el eje x. Porque las fuerzas son vectores, se puede utilizar como una representación física de los vectores. Estableciendo un sistema de fuerzas y encontrar que la fuerza adicional va a crear un equilibrio entre las fuerzas, un sistema de vectores puede ser verificado experimentalmente.
En la figura 1 se muestra el vector de  , así como los ejes x e yy el ángulo θ que
, así como los ejes x e yy el ángulo θ que  hace con el eje x.
hace con el eje x.

Figura 1 .
Para sumar o restar dos vectores, es útil describir los vectores en sus componentes x y y. El componente xes la cantidad del vector que apunta en la xdirección, que se representa matemáticamente como:
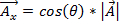 . (Ecuación 1)
. (Ecuación 1)
El componente yse representa como:
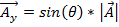 . (Ecuación 2)
. (Ecuación 2)
La magnitud de la  se define como:
se define como:
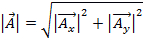 . (Ecuación 3)
. (Ecuación 3)
Para sumar o restar dos vectores, simplemente se descomponen los vectores en sus componentes x e yy luego sumar o restar, respectivamente, los componentes correspondientes.
Por ejemplo, si vector 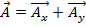 y
y 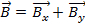 , entonces la adición de dos vectores
, entonces la adición de dos vectores  .
.
Para determinar el ángulo θ que hace que un vector con respecto al eje x, utilice la siguiente ecuación:
 . (Ecuación 4)
. (Ecuación 4)
Porque los vectores tienen magnitud y dirección, multiplicar dos vectores no es tan simple como multiplicar dos números. Hay dos formas de multiplicar vectores: producto punto y producto Cruz. El producto escalar se puede escribir como 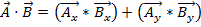 o
o 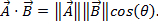 , θ es el ángulo entre dos vectores. El resultado sólo tiene una magnitud y una dirección de no. Una aplicación del producto escalar en física es el trabajo (W), donde el trabajo se define como una fuerza épocas distancia
, θ es el ángulo entre dos vectores. El resultado sólo tiene una magnitud y una dirección de no. Una aplicación del producto escalar en física es el trabajo (W), donde el trabajo se define como una fuerza épocas distancia 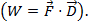 el producto cruzado de dos vectores puede escribirse como
el producto cruzado de dos vectores puede escribirse como 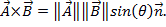 similar al producto punto, producto Cruz contiene el término
similar al producto punto, producto Cruz contiene el término  , que se define como un vector con magnitud 1 que es perpendicular a dos vectores
, que se define como un vector con magnitud 1 que es perpendicular a dos vectores  y
y  . El resultado del producto Cruz es un vector. Un ejemplo del producto Cruz en física es par
. El resultado del producto Cruz es un vector. Un ejemplo del producto Cruz en física es par  , que es el resultado de una fuerza de veces un radio
, que es el resultado de una fuerza de veces un radio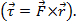
Vectores son útiles en la física porque las fuerzas como gravedad o fricción se pueden representar como vectores. En este laboratorio, la fuerza de la gravedad se utiliza para demostrar la naturaleza vectorial de las fuerzas y cómo esas fuerzas en múltiples direcciones. La fuerza de la gravedad en la superficie de la tierra se escribe como:
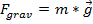 , (Ecuación 5)
, (Ecuación 5)
donde  es la masa del objeto, mientras que
es la masa del objeto, mientras que  es la aceleración de la gravedad cerca de la superficie terrestre (9,8 m/s2).
es la aceleración de la gravedad cerca de la superficie terrestre (9,8 m/s2).
1. equilibrio de fuerzas.
- La mesa de fuerza, instaló dos poleas con la misma masa hacia direcciones opuestas (diferencia de 180° de ángulo).
- La fuerza de cada uno será igual a
 . Compruebe si las dos fuerzas son igual y opuesta, examinando el anillo en el centro de la mesa de fuerza, que no debe moverse.
. Compruebe si las dos fuerzas son igual y opuesta, examinando el anillo en el centro de la mesa de fuerza, que no debe moverse. - Observe que si se añaden los componentes de los vectores asociados a estas fuerzas, el vector resultante tendrá cero magnitud. Esto es cómo determinar que todas las fuerzas están en equilibrio.
2. analíticos cálculos.
- Este laboratorio consta de tres fuerzas en equilibrio. Dos fuerzas serán conocidas, mientras que la tercera será primero encontrado analíticamente, mediante la teoría de vectores y luego experimentalmente. Para este laboratorio, mantenga
 a 0° para la duración.
a 0° para la duración. - Tenga en cuenta que si
 y
y  son conocidos y
son conocidos y  , cuando se agrega al sistema, causas ambas fuerzas para estar en equilibrio, entonces
, cuando se agrega al sistema, causas ambas fuerzas para estar en equilibrio, entonces  es de igual magnitud pero en sentido contrario de la suma (
es de igual magnitud pero en sentido contrario de la suma ( +
+  ).
). - Calcular la magnitud de la
 y
y  . Usar el hecho de que
. Usar el hecho de que  y que 1 Newton (N) es una unidad de fuerza igual a
y que 1 Newton (N) es una unidad de fuerza igual a  .
. - La teoría de vectores, calcular qué magnitud
 sería si es la suma (
sería si es la suma ( +
+  ).
). - Usando la teoría de vectores, calcular a qué ángulo
 sería si es la suma (
sería si es la suma ( +
+  ).
).
3. experimento.
- Siguiendo los valores de la primera línea de la tabla 1 para
 y
y  , configurar las dos fuerzas sobre la mesa de fuerza. Recuerde que debe mantener
, configurar las dos fuerzas sobre la mesa de fuerza. Recuerde que debe mantener  a 0°.
a 0°. - Configurar la tercera fuerza,
 , añadiendo pesos y cambiar el ángulo hasta que se alcanza el equilibrio. Registrar estos valores en la tabla 2.
, añadiendo pesos y cambiar el ángulo hasta que se alcanza el equilibrio. Registrar estos valores en la tabla 2. - Repita el paso 3.2 para cada uno de los cuatro casos.
- Determinar la diferencia porcentual del resultado analítico mediante el cálculo de la
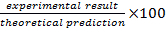 . Completa la tabla 2 con los valores calculados.
. Completa la tabla 2 con los valores calculados.
Los resultados de laboratorio se muestran en la tabla 1 y tabla 2.
Tabla 1. Programa de instalación.
| Configuración # | A | B | ||
| Masa | Ángulo de | Masa | Ángulo de | |
| 1 | 100 | 0 | 100 | 20 |
| 2 | 100 | 0 | 150 | 40 |
| 3 | 200 | 0 | 150 | 60 |
| 4 | 200 | 0 | 250 | 80 |
Tabla 2. Resultados analíticos.
| Configuración # | Magnitud (N) |
Magnitud (N) |
Ángulo de (°) |
Magnitud (N) |
Ángulo de (°) |
| 1 | 0.98 | 0.98 | 20 | 1.93 | 10 |
| 2 | 0.98 | 1.47 | 40 | 2.31 | 24 |
| 3 | 1,96 | 1.47 | 60 | 2.98 | 25 |
| 4 | 1,96 | 2.45 | 80 | 3.39 | 45 |
Tabla 3. Resultados experimentales.
| Configuración # | Magnitud experimental (N) |
Magnitud analítica (N) |
Diferencia (%) |
Ángulo experimental (°) |
Ángulo analítico (°) |
Diferencia (%) |
| 1 | 2.1 | 1.93 | 9 | 11 | 10 | 10 |
| 2 | 2.2 | 2.31 | 5 | 26 | 24 | 8 |
| 3 | 2.8 | 2.98 | 6 | 28 | 25 | 12 |
| 4 | 3.5 | 3.39 | 3 | 43 | 45 | 5 |
Los resultados del experimento están de acuerdo con los cálculos analíticos. La suma de dos vectores y el ángulo entre ellos se puede calcular usando las ecuaciones 1-5. Las ecuaciones son válidas para hacer cálculos de vectores físicos, tales como fuerza.
Un jardinero en el béisbol tiene que entender vectores para coger una pelota en movimiento. Si el jardinero sólo conocía la velocidad de la bola, podría al leftfield en vez de a la derecha y el balón se pierda. Si sólo supiera la dirección del golpe, podría cobrar, sólo para ver la bola de la vela sobre su cabeza. Si él entiende vectores, entonces tan pronto como la bola es golpeada, puede considerar la magnitud y dirección para estimar donde la bola va a ser cuando hace una captura.
Cuando un avión está en el cielo, su velocidad y dirección pueden escribirse como un vector. Cuando hay un fuerte viento, el vector viento añade al vector del plano para dar el vector resultante del sistema. Por ejemplo, si un avión está volando en el viento, la magnitud del vector resultante será menor que la magnitud inicial. Esto corresponde al plano de movimiento más lento cuando se dirige hacia el viento, que tiene sentido intuitivo.
Cuando dos objetos chocan y se pegan, su impulso final (un vector) se puede aproximar como la suma de los dos vectores del impulso inicial. Esto es una simplificación, como en el mundo real, dos objetos que chocan tienen factores adicionales a considerar, como calor o deformación de la colisión. Impulso es simplemente la masa de un objeto multiplicada por su velocidad. Si dos patinadores en hielo viajando en diferentes direcciones y velocidades diferentes chocan y aferrarse a ellos, su dirección final y la velocidad se pueden estimar en base a sus componentes del vector inicial.
En este experimento, la naturaleza del vector de fuerzas fue examinada y medida. Vectores se suman, y se determinaron la magnitud resultante y dirección tanto analítica como experimentalmente.
Saltar a...
Vídeos de esta colección:

Now Playing
Vectores en múltiples direcciones
Physics I
182.3K Vistas

Las leyes del movimiento de Newton
Physics I
75.7K Vistas

Fuerza y aceleración
Physics I
79.1K Vistas

Cinemática y movimiento de proyectiles
Physics I
72.6K Vistas

Ley de la gravitación Universal de Newton
Physics I
190.8K Vistas

Conservación del momento
Physics I
43.3K Vistas

Fricción
Physics I
52.9K Vistas

Ley de Hooke y el movimiento armónico simple
Physics I
61.3K Vistas

Diagramas de equilibrio y de cuerpo libre
Physics I
37.3K Vistas

Esfuerzo torsional
Physics I
24.3K Vistas

Inercia rotacional
Physics I
43.5K Vistas

Momento angular
Physics I
36.2K Vistas

Energía y trabajo
Physics I
49.7K Vistas

Entalpía
Physics I
60.4K Vistas

Entropía
Physics I
17.6K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados