Entropia

Fonte: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA

A segunda lei da termodinâmica é uma lei fundamental da natureza. Ele afirma que a entropia de um sistema sempre aumenta ao longo do tempo ou permanece constante em casos ideais quando um sistema está em um estado estável ou passando por um "processo reversível". Se o sistema estiver passando por um processo irreversível, a entropia do sistema sempre aumentará. Isso significa que a mudança na entropia, ΔS, é sempre maior ou igual a zero. A entropia de um sistema é uma medida do número de configurações microscópicas que o sistema pode alcançar. Por exemplo, o gás em um recipiente com volume, pressão e temperatura conhecidos pode ter um enorme número de configurações possíveis das moléculas de gás individuais. Se o recipiente for aberto, as moléculas de gás escapam e o número de configurações aumenta drasticamente, essencialmente se aproximando do infinito. Quando o recipiente é aberto, diz-se que a entropia aumenta. Portanto, a entropia pode ser considerada uma medida da "desordem" de um sistema.

Entropia é uma "propriedade estatal", que é uma quantidade que depende apenas do estado atual do sistema. As quantidades que são propriedades estaduais não dependem do caminho pelo qual o sistema chegou ao seu estado atual. Portanto, a maneira mais útil de quantificar uma propriedade estatal é medir sua mudança.

A mudança na entropia S é definida como:

ΔS = Q / T, (Equação 1)

onde Q é o calor fornecido ao sistema e T é a temperatura do sistema. No contexto da termodinâmica, o calor, como o trabalho, é definido como uma transferência de energia. Calor é energia transferida de um objeto para outro por causa de uma diferença de temperatura. Considere um banho de gelo e água a 0 °C. Se alguém fornece calor ao banho de gelo/água, parte do gelo derreterá, e o número de estados disponíveis para as moléculas de água aumentará em grande quantidade, proporcional à quantidade de calor que foi adicionada ao sistema. A entropia aumentará proporcionalmente a esse valor. A relação entre dois objetos a temperaturas diferentes foi descrita pela primeira vez por Newton.

A lei de newton de resfriamento afirma que a taxa de mudança da temperatura de algum objeto é proporcional à diferença entre sua própria temperatura e a temperatura de seu entorno. Para um objeto à temperatura T colocado em um sistema fechado à temperatura T_f,esta mudança de temperatura em função do tempo t é descrita pela equação diferencial:

dT/dt = -k(T - T_f ), (Equação 2)

onde k é uma constante que depende das características do objeto e seu entorno. A equação 1 está escrita equivalentemente como:

-k dt = dT / (T - T_f ). (Equação 3)

Integrar ambos os lados dá:

-k t = log(T - T_f ) + log C. (Equação 4)

Aplicar a função exponencial em ambos os lados da equação e, em seguida, reorganizar dá:

T - T_f = C e^-kt . (Equação 5)

Se o objeto em questão estiver a uma temperatura inicial T_i no momento t = 0:

T_i- T_f = C. (Equação 6)

Segue-se que a temperatura em função do tempo é:

T(t) =T_f + (T_i- T_f ) e^-kt . (Equação 7)

Portanto, quando um objeto quente é colocado em um sistema fechado mais frio, sua temperatura diminuirá a uma taxa exponencial. Neste sistema fechado, o calor do objeto quente Q aumentará a temperatura do ambiente mais frio e, assim, aumentará o número de estados disponíveis. Assim, a mudança na entropia, ΔS,é positiva e não zero.

1. Configuração.

1. Obtenha um elemento de aquecimento e suporte, um termômetro, um cronômetro, algumas toalhas de papel, água e um grande béquer.
2. Encha o béquer com água suficiente para que a amostra não esfrie muito rapidamente (ou seja, pelo menos 500 mL).
3. Coloque o béquer cheio de água no suporte abaixo do elemento de aquecimento e ligue-o.
4. Quando o béquer de água chegar a ferver, insira o termômetro e desligue o elemento de aquecimento.
5. Retire cuidadosamente o béquer do suporte de aquecimento e coloque-o sobre a mesa, em cima das toalhas de papel. Estes agirão como isolamento da mesa.

2. Registrando dados.

1. Comece o cronômetro e regisse a temperatura e o tempo.
2. Nos primeiros 20 minutos, faça uma medição a cada 1 minuto.
3. Para os próximos 20 minutos, faça uma medição a cada 3-5 min.
4. Registo esses valores na Tabela 1.
5. Plote os pontos de dados coletados na Tabela 1 em um gráfico de temperatura versus tempo.
6. Usando a temperatura inicial da água e quaisquer dois pontos de dados para o tempo e temperatura, resolva a Equação 7 para a constante de resfriamento k.
7. Usando este valor para k, plote Equação 7 como uma função contínua de t. Compare a função com os pontos de dados coletados.

Os resultados representativos para 680 mL de água são mostrados na Tabela 1. A constante de resfriamento k foi encontrada usando os pontos de dados na tabela e resolvendo a Equação 7. Após 35 min, T(35) = 50,6. A temperatura inicial foi de 100 °C, e a coleta de dados cessou a 28,5 °C. O uso dessas variáveis dá a seguinte equação para obter k:

50,6 = 28,5 + (100 - 28,5) e^{-k 35}. (Equação 8)

Resolver para k dá um valor k = 0,034. A curva com esta constante de resfriamento é mostrada como uma linha cinza tracejada na Figura 1,juntamente com os pontos de dados do experimento. A forma funcional da Equação 6 corresponde muito de perto aos resultados experimentais.

À medida que a água esfria, a entropia diminui, uma vez que o número de estados disponíveis para as moléculas de água diminui. A entropia do ar ambiente na sala aumenta porque o béquer de água transfere calor para as moléculas de ar ao seu redor; a entropia geral do sistema de água + ar aumenta. O número de estados que as moléculas de ar mais quentes podem ocupar é muito maior do que antes da água quente ser introduzida na sala.

Na forma diferencial, o calor dQ adicionado ou removido da água pode ser calculado usando a relação entre massa, calor específico c, e mudança de temperatura:

dQ = mc dT, (Equação 9)

onde c é conhecido por ser 4.18 J/(gK) para água. A mudança na entropia da água é então:

ΔS_água =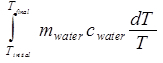

= m_água c_{d(T final} / T_inicial). (Equação 10)

Utilizando a conversão para Kelvin como K = °C + 273,15, a mudança na entropia da água é calculada como:

ΔS_água = 680 g * 4,18 J/(g K) * ln[(28,5 + 273,15)/(100 + 273,15)]

= -604 J/K.

A temperatura do ar ambiente é constante a 20,4 °C, por isso este é um processo isotémico. A mudança de entropia do ar é então:

ΔS_ar = ,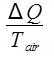

onde Q é o calor liberado pela água, que é dado pela Equação 9. A mudança na entropia do ar é então calculada como:

ΔS_ar =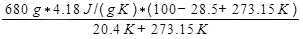

= 3337 J/K.

A mudança total na entropia do sistema de água + ar, ΔS_tot,é a soma das mudanças individuais na entropia da água e do ar ambiente:

ΔS_tot = ΔS_água +ΔS_ar (Equação 11)

= -604 J/k + 3337 J/K

= 2733 J/K.

Mesa 1. Temperaturas registradas durante o experimento.

Tempo (min s)	Temperatura da água (°C)
0 0	99.6
1 10	97.1
1 50	94.2
2 30	91.8
3 22	89
4 05	87.2
5 08	82.7
6 05	82.4
8 25	78
9 15	76.5
10 15	74.6
11 38	72.7
12 58	70.7
13 58	69.2
15 15	67.7
16 55	65.8
18 38	64
20 25	62.3
24 02	58.8
25 45	57.3
34 45	50.6
40 50	47.4
44 30	45.9
49 59	43.6
53 42	42.4
60 01	40.2
64 20	39.5
76 37	37
103 50	32.1
116 41	30.3
122 46	29.6
134 11	28.5

Figura 1. Parcela de temperatura versus tempo. Os pontos azuis indicam os dados experimentais, e a linha tracejada representa dados teóricos baseados na lei de resfriamento de Newton.

Um par de fones de ouvido mantidos em uma bolsa sempre tende a ficar atado - este é um aumento na entropia causado pelo transporte da bolsa ao redor. É necessário fazer o trabalho nos fones de ouvido para desa nó-los e diminuir a entropia (isso pode ser considerado como um "processo reversível"). O ciclo de motor de calor mais eficiente permitido pelas leis físicas é o ciclo Carnot. A segunda lei diz que nem todo o calor fornecido a um motor de calor pode ser usado para fazer o trabalho. A eficiência do Carnot define o valor limitante na fração de calor que pode ser usada. O ciclo consiste em dois processos isotemais seguidos por dois processos adiabáticos. Uma geladeira, que é essencialmente apenas uma bomba de calor, também é um exemplo clássico da segunda lei. Os refrigeradores movem o calor de um local a uma temperatura mais baixa (a "fonte") para outro local a uma temperatura mais alta (o "dissipador de calor") usando trabalho mecânico. De acordo com a segunda lei, o calor não pode fluir espontaneamente de um local mais frio para um mais quente; assim, o trabalho (energia) é necessário para a refrigeração.

A lei de newton de resfriamento foi demonstrada por um béquer cheio de água a 100 °C esfriando até a temperatura ambiente, o que levou a um aumento na entropia do sistema de ar-água. Medindo a temperatura da água em função do tempo durante um período de 135 minutos, foi possível confirmar que o resfriamento da água era exponencial na forma. A constante de resfriamento da amostra de água foi encontrada resolvendo a equação de resfriamento usando dados coletados.