Entropía

Fuente: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Departamento de física & Astronomía, Facultad de ciencias física, Universidad de California, Irvine, CA

La segunda ley de la termodinámica es una ley fundamental de la naturaleza. Se dice que la entropía de un sistema siempre aumenta con el tiempo o permanece constante en casos ideal cuando un sistema está en un estado estacionario o someterse a un "proceso reversible." Si el sistema es sometido a un proceso irreversible, la entropía del sistema siempre aumentará. Esto significa que el cambio en entropía, ΔS, es siempre mayor o igual a cero. La entropía de un sistema es una medida del número de configuraciones microscópicas que puede alcanzar el sistema. Por ejemplo, gas en un recipiente con volumen conocido, la presión y la temperatura puede tener un enorme número de configuraciones posibles de las moléculas de gas individual. Si se abre el recipiente, las moléculas del gas de escape y el número de configuraciones aumenta dramáticamente, esencialmente acercarse a infinito. Al abrir el envase, la entropía se dice que aumentar. Por lo tanto, la entropía se puede considerar una medida del "desorden" de un sistema.

Entropía es una "propiedad del estado," que es una cantidad que depende solamente del estado actual del sistema. Cantidades que son propiedades de estado no dependen de la ruta por la que el sistema llegó a su estado actual. Por lo tanto, la forma más útil cuantificar una propiedad estatal es medir su cambio.

El cambio en la entropía S se define como:

ΔS = Q / T, (Ecuación 1)

en Q es el calor suministrado al sistema y T es la temperatura del sistema. En el contexto de la termodinámica, el calor, como el trabajo, se define como una transferencia de energía. El calor es energía transferida de un objeto a otro debido a una diferencia de temperatura. Considerar un baño de hielo y agua a 0 ° C. Si uno provee calor para el baño de hielo/agua, algunos de los hielos se derretirán y aumentará el número de Estados disponibles para las moléculas de agua por una gran cantidad, proporcional a la cantidad de calor agregado al sistema. La entropía entonces aumentará proporcionalmente a esta cantidad. La relación entre dos objetos a diferentes temperaturas fue descrita por Newton.

Ley de enfriamiento de Newton indica que la tasa de cambio de la temperatura de un objeto es proporcional a la diferencia entre su propia temperatura y la temperatura de su entorno. Para un objeto a temperatura que t colocado en un sistema cerrado a temperatura T_f, este cambio de temperatura como función del tiempo t es descrita por la ecuación diferencial:

dT/dt = -k (T - T_f ), (ecuación 2)

que k es una constante que depende de las características del objeto y su entorno. Ecuación 1 equivalente es escrita como:

-k dt = dT / (T - T_f ). (Ecuación 3)

Integrando ambos lados da:

-t k = log (T - T_f ) + sesión C. (Ecuación 4)

Aplicando la función exponencial a ambos lados de la ecuación y luego reorganizar dan:

T - T_f = C e^-kt . (Ecuación 5)

Si el objeto en cuestión está a una temperatura inicial T en tiempo t = 0:

T_i- T_f = C. (Ecuación 6)

Se deduce que la temperatura en función del tiempo es:

T(t) = T_f (T_i- T_f ) e^-kt . (Ecuación 7)

Por lo tanto, cuando se coloca un objeto caliente en un sistema cerrado más frío, su temperatura disminuirá a un ritmo exponencial. En este sistema cerrado, el calor del objeto caliente Q aumentará la temperatura del entorno más fresco y así aumentar el número de Estados disponibles. Así, el cambio en entropía, ΔS, es positivo y distinto de cero.

1. programa de instalación.

1. Obtener un elemento calefactor y soporte, un termómetro, un cronómetro, algunas toallas de papel, agua y un vaso de precipitados grande.
2. Llene el vaso con suficiente agua para que la muestra no se enfríe demasiado rápidamente (es decir, al menos 500 mL).
3. Coloque el vaso lleno de agua en el soporte por debajo del elemento de calefacción y encender.
4. Una vez que el vaso de agua llega a hervir, introducir el termómetro y apaga el elemento calefactor.
5. Con cuidado retire el vaso del soporte de calefacción y colocar sobre la mesa, encima de las toallas de papel. Estos actuarán como aislante de la tabla.

2. datos de la grabación.

1. Comenzar el cronómetro y registrar la temperatura y el tiempo.
2. Para los primeros 20 minutos, tomar una medida sobre cada 1 minuto.
3. Para los próximos 20 minutos, tomar una medida sobre cada 3-5 minutos.
4. Registrar estos valores en la tabla 1.
5. Trazar los puntos de datos que fueron recogidos en la tabla 1 en un gráfico de temperatura versus tiempo.
6. Utilizando la temperatura inicial del agua y de cualquier dos puntos para el tiempo y la temperatura, resolver la ecuación 7 para el enfriamiento constante k.
7. Utilizando este valor de k, parcela 7 ecuación como una función continua de t. Comparar la función con los puntos de datos que fueron recogidos.

Resultados representativos de 680 mL de agua se muestran en la tabla 1. El enfriamiento constante k fue encontrado usando los puntos de datos en la tabla y resolver la ecuación 7. Después de 35 min, T(35) = 50,6. La temperatura inicial era de 100 ° C y recopilación de datos dejó a 28,5 ° C. El uso de estas variables da la siguiente ecuación para obtener k:

50.6 = 28,5 + (100-28.5) e^{-k 35}. (Ecuación 8)

Resolviendo para k le da un valor k = 0.034. La curva con esta constante enfriamiento se muestra como una línea gris punteada en la figura 1, junto con los puntos de datos del experimento. La forma funcional de la ecuación 6 coincide muy de cerca con los resultados experimentales.

Como el agua se enfría, la entropía disminuye, puesto que el número de Estados disponibles para la disminución de las moléculas de agua. La entropía del aire ambiente en la habitación aumenta porque el vaso de agua transfiere calor a las moléculas de aire que la rodea; la entropía total del agua + aire sistema aumenta. El número de Estados que pueden ocupar las moléculas de aire más caliente ahora es mucho mayor que antes de que el agua caliente se introdujo a la sala.

En forma diferencial, se puede calcular usando la relación entre masa, calor específico c, la d calorQ agregan o quitan del agua y cambio de temperatura:

dQ = mc dT, (ecuación 9)

donde c es conocido por ser J/(gK) 4.18 para agua. El cambio en entropía del agua es entonces:

ΔS_agua =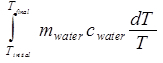

= m_agua c_agua ln (T final/T_inicial). (Ecuación 10)

Utilizando la conversión a Kelvin k = ° C + 273.15, el cambio en la entropía del agua se calcula como:

ΔS_agua = 680 g * 4.18 J /(g K) * ln [(28.5 + 273.15) / (100 + 273.15)]

=-604 J/K.

La temperatura del aire es constante a 20,4 ° C, por lo que se trata de un proceso isotérmico. El cambio de entropía del aire es entonces:

ΔS_aire = ,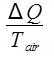

donde Q es el calor liberado por el agua, que es dado por ecuación 9. El cambio de entropía del aire se calcula entonces como:

ΔS_aire =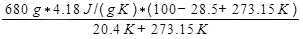

= 3337 J/K.

El cambio total en la entropía del agua + aire sistema, ΔS_tot, es la suma de los cambios individuales en la entropía del agua y del aire ambiente:

ΔS_tot = ΔS_agua + ΔS_aire (ecuación 11)

=-604 J/k + J 3337/K

= 2733 J/K.

Tabla 1. Las temperaturas registradas durante el experimento.

Tiempo (min s)	Temperatura (° C)
0 0	99.6
1 10	97.1
1 50	94.2
2 30	91,8
3 22	89
4 05	87.2
5 08	82.7
6 05	82.4
8 25	78
9 15	76.5
10 15	74.6
11 38	72.7
12 58	70.7
13 58	69.2
15 15	67.7
16 55	65.8
18 38	64
20 25	62.3
24 02	58.8
25 45	57.3
34 45	50,6
40 50	47.4
44 30	45.9
49 59	43.6
53 42	42.4
60 01	40.2
64 20	39,5
76 37	37
50 de 103	32.1
41 de 116	30.3
46 de 122	29.6
134 11	28.5

Figura 1 . Parcela de temperatura versus tiempo. Los puntos azules indican los datos experimentales, y la línea discontinua representa datos teóricos basados en la ley de enfriamiento de Newton.

Un par de auriculares que guardó en una bolsa siempre tiende a ser anudada-este es un aumento de entropía causado por la bolsa alrededor. Es necesario trabajarlos en los auriculares a un nudo y disminución de la entropía (esto puede ser considerado como un "proceso reversible"). El más eficiente ciclo de motor de calor permitido por las leyes físicas es el ciclo de Carnot. La segunda ley afirma que no todo el calor suministrado a un motor de calor puede utilizarse para hacer el trabajo. La eficiencia de Carnot establece el valor límite en la fracción de calor que puede ser utilizado. El ciclo consta de dos procesos isotérmicos seguidos de dos procesos adiabáticos. Un refrigerador, que es esencialmente sólo una bomba de calor, también es un ejemplo clásico de la segunda ley. Refrigeradores mover calor de un lugar a baja temperatura (la "fuente") a otra ubicación en una temperatura más alta (el "disipador de calor") utilizando el trabajo mecánico. Según la segunda ley, calor no puede fluir espontáneamente de un lugar frío a uno más caliente; así, el trabajo (energía) es necesaria para la refrigeración.

Ley de enfriamiento de Newton fue demostrado por un vaso de precipitados lleno de agua a 100 ° C, enfriar a temperatura ambiente, lo que condujo a un aumento en la entropía del sistema agua-aire. Mediante la medición de la temperatura del agua en función del tiempo durante un período de 135 min, fue posible confirmar que el enfriamiento del agua es en forma exponencial. La constante de enfriamiento de la muestra de agua fue encontrada por resolver la ecuación de enfriamiento usando los datos recogidos.