フックの法則と簡単な調和運動

ソース:ミッチェル ・ ウィン博士は Ketron、 Asantha Cooray、PhD、物理教室 & 天文学、物理的な科学の学校、カリフォルニア大学、アーバイン、カリフォルニア州

潜在的なエネルギーは、物理学における重要な概念です。潜在的なエネルギーは、その周辺を基準にしてオブジェクトの位置に依存する力に関連付けられているエネルギーです。重力ポテンシャル エネルギー、別のビデオで説明されて、関連付けられているエネルギーは、地上オブジェクトの高さに比例します。同様に、直接ばねの変位に比例してそのリラックスした状態から春の潜在的なエネルギーの定義することが可能です。ストレッチまたは圧縮されたスプリング オブジェクトに仕事をする能力があり、潜在的なエネルギーがあります。「仕事をする能力」は、エネルギー基本的な定義としてしばしば引用されています。

このビデオはばねに格納されている潜在的なエネルギーを示します。それはまたばね、またはフックの法則の復元力方程式を確認します。異なる弾力性のスプリングのバネ定数が違います。フックの法則を検証してバネ定数を用いて様々 な重みを中断された春に接続して、結果として得られる変位測定します。

いずれかで春の圧縮または伸ばされた位置を保持している誰かまたは何か春に力を発揮することが必要です。この力は、春の Δy、変位に比例。ターンでは、春を一層同輩および反対力します。

F = k Δy、(式 1)

kが「ばね剛性定数」と呼ばれるこれは「復元力」負の符号によって示されるばね変位、反対の方向に力を発揮するために呼びます。方程式 1はフックの法則として知られています。

簡単な調和運動は、フックの法則は、平衡からの変位に比例する復元力があるときに発生します。ニュートン第 2 法律, F = ma、および時間経過に伴って変位の二次導関数は、加速度を方程式 1として書き換えることができます。

m (d²y/dt²) -k yを =。(式 2)

この二次微分を解決するよく知られています。

y(t) = (ωt + φ)、罪 (式 3)

A は波状、ω = (k/m) の^1/2、および位相角φがシステムの初期条件に依存します。式 3の形の方程式は、単振動と呼ばれるものについて説明します。周期 T、周波数f、および定数 ω によって関連です。

Ω = 2 πf = 2 π/t. (式 4)

したがって、周期 T で与えられます。

T = 2 π (m/k)^1/2。(式 5)

T は振動の振幅 A には依存しないことに注意してください。したがって、重量が垂直から中断春からハングした場合振動の結果の期間は添付の重量の平方根に比例します。

春を伸ばすために必要な作業距離 y は W = <F> y、どこ <F> 文字列を伸ばすために必要な平均の力です。Fはyで直線的なので平均は平衡 (= 0) で力だけとyの力。

<F> ½ = [0 + ky]。(式 6)

仕事とこのように弾性ポテンシャル エネルギーを PE、として記述できます。

PE = ½ k y²。(関係式 7)

ばねの潜在的なエネルギーは、この演習で測定されます。

1. バネ定数とバネのポテンシャル エネルギーを測定し、質量と振動周期 t. 間の関係を確認

1. 知られているばね定数、春に付けるスタンド、少なくとも 5 重春、メートルの棒およびストップウォッチに添付することができますさまざまな大衆のばねを取得します。
2. スタンドの強固な基盤を固定し、春をスタンドに取り付けます。テーブルまたは地面を押すことがなくストレッチするそれをバネの下の十分な部屋があることを確認します。
3. 大衆のそれぞれに対して、地球の重力によってばねにかかる力を計算 (F = mg)。少なくとも大規模な重量を開始します。表 1にこれらの値を記録します。
4. 春は国連伸ばされた位置でどれくらいテーブルの表面の高さを測定します。
5. 春には少なくとも大規模な体重を添付し、変位 Δy1 を測定 (図 1参照)。表 1にこの変位を記録します。
6. 接続されている重量、それを解放する前に重量を少し持ち上げます。振動の動きを観察します。ストップウォッチと周期 T を測定します。正確な測定のため複数の期間の時間を記録し、観察期間の数によってその時間を分割します。この複数回行うし、表 1の周期 T の測定平均時間を記録します。
7. 質量の増加の順序で 1.5 〜 1.6 大衆のすべての手順を繰り返します。
8. ごとに異なる質量ばねの潜在的なエネルギーを計算し、表 1にそれらを記録します。
9. 力Fを変位 Δyの関数としてプロットします。式 1によるとこれは線形はずです。ラインを斜面に合います。この坂は、ばね定数 k 比較春の既知の値を測定値に対応します。
10. 振動の周期 T が大衆; の各する必要があります知られているばね定数と式 5を使用して、計算します。表 1にそれらを報告します。1.6 の手順でストップウォッチで測定した T に比較します。

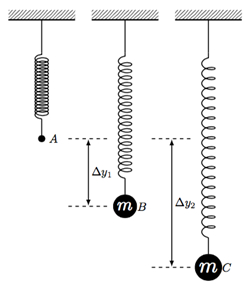
図 1: Srping 振動

定数kのばねで実施した実験の代表的な結果 = 10 N/m は、表 1に示します。変位 ΔyとFのプロットは、以下の図 2にプロットされます。線形関数は、行に合うし、直線の傾きが許容誤差内のバネ定数と等しい。結果の直線性は、フックの法則 (式 1) の妥当性を示しています。

表 1春に添付されている質量を振動の周期 T がどのように関連しているかを確認するを確認します。重い、長い期間、春に接続されている質量となります、質量 (式 5) の平方根に比例。なおより大きい固まりは春の終わりにアタッチしている場合、春はさらに伸びとがあります。乗変位平衡 (方程式 7) からの機能である、システムの潜在的なエネルギーが大きい。期間はより大きい固まりのため長いこと理にかなって-平衡から遠い春を転置するので、長い距離を移動する時間がかかります。
表 1。結果。

質量 (kg)	重量/ F (N)	Δy (m)	PE (J)	T 測定 (s)	計算 T (s)
0.5	4.9	0.49	2.4	1.3	1.4
0.75	7.4	0.74	5.4	1.6	1.7
1	9.8	0.98	9.6	1.9	1.9
1.5	14.7	1.5	21.6	2.5	2.4
2	19.6	2	38.4	2.9	2.8

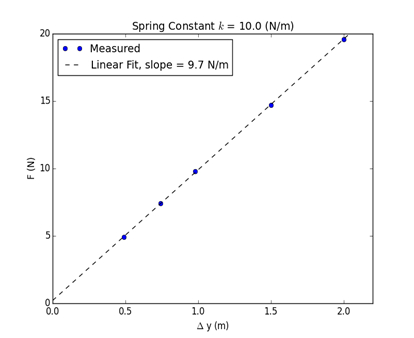
図 2: 変位対応用力 (N) のプロット。

ばねの使用は、私たちの日常生活の中でユビキタスです。現代の車のサスペンションは、正しく制振ばねから作られます。バネ定数の知識が必要です。スムーズなキャデラックの乗り物は、低いばね定数のスプリングを使用し、乗り心地は"mushier"。高性能車より良いハンドリングのため高いばね定数とスプリングを使用します。どのくらい「バウンス」は時に必要なボードからダイビングに応じて異なるスプリング定数のばねを持つダイビング ボードが作られています。ロック クライミング ロープは、登山家の滝を登りながら、ロープが地面を押したから彼女を救うだけでなく、秋を湿らせて、その弾力性と、またそれも少し弾力性。小さくクライミング ロープのバネ定数、もっと密接にそれのようなバンジー ジャンプします。

本研究ではさまざまな大きさの力のアプリケーションから生じるばねの変位を測定しました。フックの法則の妥当性は、ぶら下げばねに加えられた力の関数として生じる変位をプロットによって確認されました。振動も春に接続されている質量の二乗根に比例して期間が観察された.