Hooke's Law and Simple Harmonic Motion
Overview
Source: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA
Potential energy is an important concept in physics. Potential energy is the energy associated with forces that depend upon the position of an object relative to its surroundings. Gravitational potential energy, which is discussed in another video, is the energy associated that is directly proportional to the height of an object above the ground. Similarly, it is possible to define spring potential energy, which is directly proportional to the displacement of a spring from its relaxed state. A stretched or compressed spring has potential energy, as it has the ability to do work upon an object. The “ability to do work” is often quoted as the fundamental definition of energy.
This video will demonstrate the potential energy stored in springs. It will also verify the restoring force equation of springs, or Hooke’s Law. The spring constant is different for springs of different elasticities. Hooke’s law will be verified and the spring constant measured by attaching varying weights to a suspended spring and measuring the resulting displacements.
Principles
Holding a spring in either its compressed or stretched position requires that someone or something exerts a force on the spring. This force is directly proportional to the displacement, Δy, of the spring. In turn, the spring will exert an equal and opposite force:
F = -k Δy, (Equation 1)
where k is called the “spring stiffness constant.” This is often referred to as a “restoring force” because the spring exerts a force in the direction opposite to the displacement, indicated by the negative sign. Equation 1 is known as Hooke’s law.
Simple harmonic motion will occur whenever there is a restoring force that is proportional to the displacement from equilibrium, as is in Hooke’s law. From Newton’s second law, F = ma, and recognizing that the acceleration a is the second derivative of displacement with respect to time, Equation 1 can be rewritten as:
m (d2y/dt2) = -k y. (Equation 2)
The solution to this second-order differential is well known to be:
y(t) = A sin(ωt + φ), (Equation 3)
where A is the amplitude of oscillation, ω = (k/m)1/2, and the phase angle φ depends upon the initial conditions of the system. Equations in the form of Equation 3 describe what is called simple harmonic motion. The period T, the frequency f, and the constant ω are related by:
ω = 2πf = 2π/T. (Equation 4)
Thus, the period T is given by:
T = 2π (m/k)1/2. (Equation 5)
Note that T does not depend upon the amplitude A of oscillation. Therefore, if a weight is hung from a spring suspended from the vertical, the resulting period of oscillation would be proportional to the square root of the attached weight.
The work required to stretch the spring a distance y is W = <F> y, where <F> is the average force required to stretch the string. Since F is linear in y, the average is just the force at equilibrium (= 0) and the force at y:
<F> = ½ [0 + ky]. (Equation 6)
The work done and thus the elastic potential energy, PE, can be written as:
PE = ½ k y2. (Equation 7)
The potential energy of a spring will be measured in this lab.
Procedure
1. Measure the spring constant and potential energy of a spring and confirm the relationship between the mass and oscillatory period T.
- Obtain a spring with a known spring constant, a stand to attach the spring to, at least 5 weights of varying masses that can be attached to the spring, a meter stick, and a stopwatch.
- Secure the stand to a solid foundation and attach the spring to the stand. Make sure that there is enough room below the spring for it to stretch without hitting the table or ground.
- For each of the masses, calculate the force exerted on the spring by the Earth's gravitational force (F = mg). Start with the least-massive weight. Record these values in Table 1.
- Measure how high above the surface of the table the spring is while in its un-stretched position.
- Attach the least-massive weight to the spring and measure the displacement Δy1 (see Figure 1). Record this displacement in Table 1.
- With the weight attached, slightly raise the weight before releasing it. Observe the oscillatory motion. Measure the period T with a stopwatch. For a more accurate measurement, record the time for multiple periods and divide that time by the number of periods observed. Do this multiple times and record the average time measured for the period T in Table 1.
- Repeat steps 1.5-1.6 for all of the masses, in order of increasing mass.
- Calculate the potential energy of the spring for each of the different masses and record them in Table 1.
- Plot the force F as a function of displacement Δy. According to Equation 1, this should be linear. Fit a slope to the line. This slope will correspond to the spring constant k. Compare the measured value to the known value of the spring.
- Using the known spring constant and Equation 5, calculate what the period T of oscillation should be for each of the masses; report them in Table 1. Compare them to the T that was measured with a stopwatch in step 1.6.
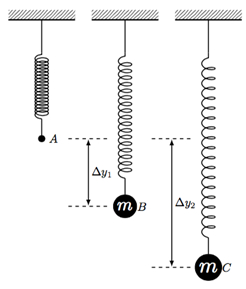
Figure 1: Srping oscillation,
Results
Representative results of the experiment, conducted with a spring of constant k = 10 N/m, are shown in Table 1. The plot of F versus the displacement Δy is plotted below in Figure 2. The linear function is fit with a line, and the slope of the line is equal to the spring constant, within a margin of error. The linearity of the result shows the validity of Hooke’s law (Equation 1).
Inspect Table 1 to see how the period T of oscillation is related to the mass that is attached to the spring. The heavier the mass attached to the spring, the longer the period will be, as it is proportional to the square root of the mass (Equation 5). Also, note that when a larger mass is attached to the end of the spring, the spring will be stretched further. The potential energy of the system is larger, as it is a function of the squared displacement from equilibrium (Equation 7). It makes sense that the period is longer for a larger mass—because the spring is displaced further from equilibrium, it will take longer to travel that longer distance.
Table 1. Results.
| Mass (kg) | Weight / F (N) | Δy (m) | PE (J) | T measured (s) | T calculated (s) |
| 0.5 | 4.9 | 0.49 | 2.4 | 1.3 | 1.4 |
| 0.75 | 7.4 | 0.74 | 5.4 | 1.6 | 1.7 |
| 1 | 9.8 | 0.98 | 9.6 | 1.9 | 1.9 |
| 1.5 | 14.7 | 1.5 | 21.6 | 2.5 | 2.4 |
| 2 | 19.6 | 2 | 38.4 | 2.9 | 2.8 |
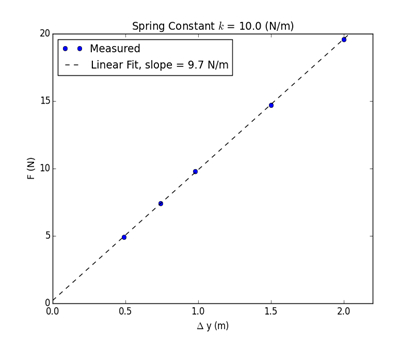
Figure 2: Plot of applied force (N) versus displacement.
Application and Summary
The use of springs is ubiquitous in our everyday lives. The suspension of modern cars is made from springs that are properly damped. This requires knowledge of the spring constants. For smoother Cadillac rides, springs with a lower spring constant are used, and the ride is “mushier.” High-performance cars use springs with a higher spring constant for better handling. Diving boards are also made with springs of different spring constants, depending upon how much “bounce” is desired when diving off the board. Rock climbing ropes are also slightly elastic, so if a climber falls while climbing, the rope will not only save her from hitting the ground, but it will also dampen the fall with its elasticity. The smaller the spring constant of a climbing rope, the more closely it resembles bungee jumping.
In this study, the displacement of a spring resulting from the application of forces of varying magnitudes was measured. The validity of Hooke’s law was verified by plotting the resulting displacements as a function of the force exerted upon the hanging spring. Oscillatory motion was also observed, with periods proportional to the square root of the mass attached to the spring.
Skip to...
Videos from this collection:

Now Playing
Hooke's Law and Simple Harmonic Motion
Physics I
61.3K Views

Newton's Laws of Motion
Physics I
75.7K Views

Force and Acceleration
Physics I
79.1K Views

Vectors in Multiple Directions
Physics I
182.3K Views

Kinematics and Projectile Motion
Physics I
72.6K Views

Newton's Law of Universal Gravitation
Physics I
190.8K Views

Conservation of Momentum
Physics I
43.3K Views

Friction
Physics I
52.9K Views

Equilibrium and Free-body Diagrams
Physics I
37.3K Views

Torque
Physics I
24.3K Views

Rotational Inertia
Physics I
43.5K Views

Angular Momentum
Physics I
36.2K Views

Energy and Work
Physics I
49.7K Views

Enthalpy
Physics I
60.4K Views

Entropy
Physics I
17.6K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved