Lei de Hooke e Movimento Harmônico Simples

Fonte: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA

Energia potencial é um conceito importante na física. Energia potencial é a energia associada a forças que dependem da posição de um objeto em relação ao seu entorno. A energia potencial gravitacional, que é discutida em outro vídeo, é a energia associada que é diretamente proporcional à altura de um objeto acima do solo. Da mesma forma, é possível definir a energia potencial da primavera, que é diretamente proporcional ao deslocamento de uma nascente de seu estado relaxado. Uma mola esticada ou compactada tem energia potencial, pois tem a capacidade de trabalhar sobre um objeto. A "capacidade de fazer o trabalho" é frequentemente citada como a definição fundamental de energia.

Este vídeo demonstrará a energia potencial armazenada em molas. Também verificará a equação da força restauradora das molas, ou a Lei de Hooke. A constante da mola é diferente para molas de diferentes elasticidades. A lei de Hooke será verificada e a constante de mola medida anexando pesos variados a uma mola suspensa e medindo os deslocamentos resultantes.

Segurar uma mola em sua posição compactada ou esticada requer que alguém ou algo exerça uma força na mola. Esta força é diretamente proporcional ao deslocamento, Δy, da primavera. Por sua vez, a mola exercerá uma força igual e oposta:

F = -k Δy,(Equação 1)

onde k é chamado de "constante da rigidez da primavera". Isso é frequentemente referido como uma "força restauradora" porque a mola exerce uma força na direção oposta ao deslocamento, indicado pelo sinal negativo. A equação 1 é conhecida como lei de Hooke.

Movimento harmônico simples ocorrerá sempre que houver uma força restauradora proporcional ao deslocamento do equilíbrio, como está na lei de Hooke. Da segunda lei de Newton, F = ma, e reconhecendo que a aceleração a é a segunda derivada de deslocamento em relação ao tempo, a Equação 1 pode ser reescrita como:

m (d²y/dt²) = -k y. (Equação 2)

A solução para este diferencial de segunda ordem é bem conhecida por ser:

y(t) = Um pecado (ωt + φ), (Equação 3)

onde A é a amplitude da oscilação, ω = (k/m)^1/2, e o ângulo de fase φ depende das condições iniciais do sistema. Equações na forma da Equação 3 descrevem o que é chamado de simples movimento harmônico. O período T, a frequência fe a constante ω estão relacionados por:

ω = 2πf = 2π/T. (Equação 4)

Assim, o período T é dado por:

T = 2π (m/k)^1/2. (Equação 5)

Note que T não depende da amplitude A da oscilação. Portanto, se um peso for pendurado em uma mola suspensa da vertical, o período resultante de oscilação seria proporcional à raiz quadrada do peso preso.

O trabalho necessário para esticar a mola a distância y é W = <F> y, onde <F> é a força média necessária para esticar a corda. Uma vez que F é linear em y , a média é apenasa força no equilíbrio (= 0) e a força em y:

<F> = 1/2 [0 + ky]. (Equação 6)

O trabalho feito e, portanto, a energia potencial elástica, PE, podem ser escritos como:

PE = 1/2 k y². (Equação 7)

A energia potencial de uma mola será medida neste laboratório.

1. Meça a energia constante e potencial da mola e confirme a relação entre a massa e o período oscilatório T.

1. Obtenha uma mola com uma constante de mola conhecida, um suporte para anexar a mola a pelo menos 5 pesos de massas variadas que podem ser anexadas à mola, uma vara de medidor e um cronômetro.
2. Fixar o suporte a uma base sólida e anexar a mola ao suporte. Certifique-se de que há espaço suficiente abaixo da mola para que ele se estique sem bater na mesa ou no chão.
3. Para cada uma das massas, calcule a força exercida na primavera pela força gravitacional da Terra (F = mg). Comece com o peso menos massivo. Registo esses valores na Tabela 1.
4. Meça o quão alto acima da superfície da tabela a mola está enquanto estiver em sua posição não esticada.
5. Conecte o peso menos massivo à mola e meça o deslocamento Δy1 (ver Figura 1). Registo este deslocamento na Tabela 1.
6. Com o peso preso, aumente ligeiramente o peso antes de soltá-lo. Observe o movimento oscilatório. Meça o período T com um cronômetro. Para uma medição mais precisa, regise o tempo de múltiplos períodos e divida esse tempo pelo número de períodos observados. Faça isso várias vezes e regise o tempo médio medido para o período T na Tabela 1.
7. Repita os passos 1.5-1.6 para todas as massas, em ordem de aumento de massa.
8. Calcule a energia potencial da mola para cada uma das diferentes massas e grave-as na Tabela 1.
9. Plote a força F em função do deslocamento Δy. De acordo com a Equação 1,isso deve ser linear. Coloque uma inclinação na linha. Esta inclinação corresponderá à constante de primavera k. Compare o valor medido com o valor conhecido da mola.
10. Utilizando a constante de mola conhecida e a Equação 5,calcule qual deve ser o período T de oscilação para cada uma das massas; denunciá-los na Tabela 1. Compare-os com o T que foi medido com um cronômetro na etapa 1.6.

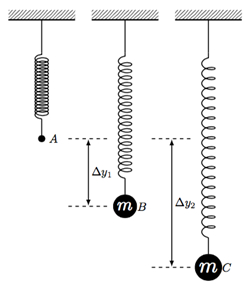
Figura 1: Oscilação de Srping,

Os resultados representativos do experimento, realizados com uma mola de k constante = 10 N/m, são mostrados na Tabela 1. O enredo de F versus o deslocamento Δy é plotado abaixo na Figura 2. A função linear é adequada com uma linha, e a inclinação da linha é igual à constante da mola, dentro de uma margem de erro. A linearidade do resultado mostra a validade da lei de Hooke(Equação 1).

Inspecione a Tabela 1 para ver como o período T de oscilação está relacionado com a massa que está presa à mola. Quanto maior a massa anexada à mola, maior será o período, pois é proporcional à raiz quadrada da massa(Equação 5). Além disso, note que quando uma massa maior é anexada ao final da primavera, a mola será esticada ainda mais. A energia potencial do sistema é maior, pois é uma função do deslocamento quadrado do equilíbrio(Equação 7). Faz sentido que o período seja mais longo para uma massa maior — porque a mola é deslocada mais longe do equilíbrio, levará mais tempo para percorrer essa distância mais longa.
Mesa 1. Resultados.

Massa (kg)	Peso / F (N)	Δy (m)	PE (J)	T medido (s)	T calculado (s)
0.5	4.9	0.49	2.4	1.3	1.4
0.75	7.4	0.74	5.4	1.6	1.7
1	9.8	0.98	9.6	1.9	1.9
1.5	14.7	1.5	21.6	2.5	2.4
2	19.6	2	38.4	2.9	2.8

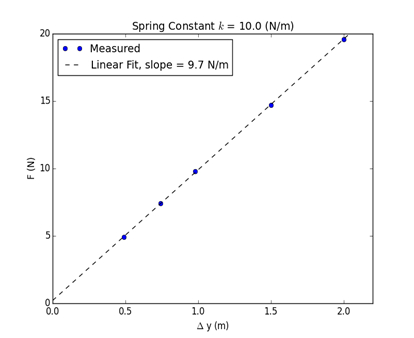
Figura 2: Parcela da força aplicada (N) versus deslocamento.

O uso de molas é onipresente em nossas vidas cotidianas. A suspensão de carros modernos é feita de molas que são devidamente amortecidos. Isso requer conhecimento das constantes da primavera. Para passeios cadillac mais suaves, molas com uma constante de mola mais baixa são usadas, e o passeio é "mushier". Carros de alto desempenho usam molas com uma maior constante de mola para melhor manuseio. Pranchas de mergulho também são feitas com molas de diferentes constantes de mola, dependendo da quantidade de "salto" desejada ao mergulhar fora da prancha. Cordas de escalada também são ligeiramente elásticas, por isso, se um alpinista cair enquanto sobe, a corda não só vai salvá-la de bater no chão, mas também vai amortecer a queda com sua elasticidade. Quanto menor a constante de mola de uma corda de escalada, mais se assemelha ao bungee jumping.

Neste estudo, foi medido o deslocamento de uma mola resultante da aplicação de forças de magnitudes variadas. A validade da lei de Hooke foi verificada plotando os deslocamentos resultantes em função da força exercida sobre a mola suspensa. Também foi observado movimento oscilatório, com períodos proporcionais à raiz quadrada da massa presa à mola.