Reibung
Überblick
Quelle: Nicholas Timmons, Asantha Cooray, PhD, Department of Physics & Astronomie, School of Physical Sciences, University of California, Irvine, CA
Das Ziel dieses Experiments ist die physikalische Natur der zwei Arten von Reibung (z. B. statische und kinetische) zu untersuchen. Das Verfahren beinhaltet die Reibungskoeffizienten für Objekte horizontal verschieben sowie auf einer schiefen Ebene zu messen.
Reibung ist nicht vollständig verstanden, aber es ist experimentell ermittelt, proportional zur Normalkraft auf ein Objekt ausgeübt werden. Wenn ein Mikroskop auf zwei Flächen, die in Kontakt sind vergrößert, würde es zeigen, dass ihre Oberfläche sehr rau in kleinem Maßstab sind. Dadurch wird verhindert, dass die Oberflächen leicht aneinander vorbei gleiten. Die Wirkung von rauen Oberflächen mit die elektrischen Kräfte zwischen den Atomen in den Materialien kombinieren kann die Reibungskraft entfallen.
Es gibt zwei Arten von Reibung. Haftreibung liegt vor, wenn ein Objekt sich nicht bewegt und etwas Kraft erforderlich ist, um das Objekt in Bewegung. Kinetische Reibung liegt vor, wenn ein Objekt bewegt sich schon, aber aufgrund der Reibung zwischen den Gleitflächen verlangsamt.
Grundsätze

Abbildung 1.
Abbildung 1 zeigt die vier Kräfte, die auf ein Objekt, das auf einer horizontalen Ebene sitzt. 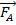 einige horizontale Krafteinwirkung entspricht.
einige horizontale Krafteinwirkung entspricht.  ist die Schwerkraft auf das Objekt, das gleichermaßen aber in die entgegengesetzte Richtung von der Normalkraft abgestimmt ist,
ist die Schwerkraft auf das Objekt, das gleichermaßen aber in die entgegengesetzte Richtung von der Normalkraft abgestimmt ist, 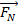 . Die Normalkraft ist ein Ergebnis einer Oberfläche, die auf ein Objekt im Gegensatz zu Schwerkraft. Die Normalkraft erklärt, warum ein Buch nicht einfach fällt durch den Tisch ruht sich auf. Zu guter Letzt gegen die einwirkende Kraft ist die Reibungskraft,
. Die Normalkraft ist ein Ergebnis einer Oberfläche, die auf ein Objekt im Gegensatz zu Schwerkraft. Die Normalkraft erklärt, warum ein Buch nicht einfach fällt durch den Tisch ruht sich auf. Zu guter Letzt gegen die einwirkende Kraft ist die Reibungskraft, 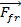 . Die Reibungskraft ist proportional zur Normalkraft:
. Die Reibungskraft ist proportional zur Normalkraft:
 , (Gleichung 1)
, (Gleichung 1)
wo  ist der Reibungskoeffizient.
ist der Reibungskoeffizient.
Der Reibungskoeffizient muss experimentell gemessen werden und ist eine Eigenschaft, die die beiden Materialien abhängt, die in Kontakt sind. Es gibt zwei Arten von Reibungskoeffizienten: kinetische Reibung,  , wenn Objekte bereits in Bewegung und Haftreibung sind,
, wenn Objekte bereits in Bewegung und Haftreibung sind, 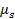 , wenn Objekte in Ruhe und eine gewisse Kraft benötigen zu bewegen. Für ein Objekt gleiten entlang eines Pfades, die Normalkraft ist gleich dem Gewicht
, wenn Objekte in Ruhe und eine gewisse Kraft benötigen zu bewegen. Für ein Objekt gleiten entlang eines Pfades, die Normalkraft ist gleich dem Gewicht  des Objekts. Daher hängt die Reibungskraft nur die Koeffizienten und die Masse eines Objekts.
des Objekts. Daher hängt die Reibungskraft nur die Koeffizienten und die Masse eines Objekts.
Wenn das Objekt auf einer schiefen Ebene, dann die Normalkraft ist 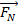 steht senkrecht auf der Steigung und ist nicht gleich und entgegengesetzt zu dem Gewicht
steht senkrecht auf der Steigung und ist nicht gleich und entgegengesetzt zu dem Gewicht  wie in Abbildung 2ersichtlich.
wie in Abbildung 2ersichtlich.

Abbildung 2.
In diesem Fall nur eine Komponente des  ist gleichbedeutend mit der Normalkraft abhängig von dem Winkel θ:
ist gleichbedeutend mit der Normalkraft abhängig von dem Winkel θ:
 . (Gleichung 2)
. (Gleichung 2)
Der Winkel der Ruhe 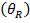 ist definiert als der Punkt an dem der Schwerkraft auf einem Objekt überwindet der statische Reibungskraft und das Objekt beginnt eine schiefe Ebene hinunter. Eine gute Näherung für den Winkel des Ausruhens ist:
ist definiert als der Punkt an dem der Schwerkraft auf einem Objekt überwindet der statische Reibungskraft und das Objekt beginnt eine schiefe Ebene hinunter. Eine gute Näherung für den Winkel des Ausruhens ist:
 . (Gleichung 3)
. (Gleichung 3)
In dieser Übungseinheit werden zwei Metall-Pfannen verwendet werden Materialien mit verschiedenen Reibungskoeffizienten vertreten. Block A haben eine Schleifpapier unten, die einen höheren Reibwert führen wird, während Block B eine glatte Metall Unterseite haben wird.
Verfahren
1. Messen Sie den Reibungskoeffizienten.
- Jeder Block eine 1.000-g-Gewicht hinzu und Nutzung einer Skala zu messen die Massen der Blöcke A und B, einschließlich die added Mass.
- Schließen Sie die Kraft Skalierung A. ziehen Sie die Skala horizontal zu blockieren und beachten die Lesung, kurz bevor der Block beginnt zu rutschen. Kurz bevor es beginnt zu rutschen, ist der Höchstbetrag der Haftreibung Widerstand gegen die Bewegung. Die Kraft-Lesung zur Berechnung verwenden
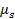 für Block A. Tun Sie dies fünf Mal und notieren Sie den Durchschnittswert.
für Block A. Tun Sie dies fünf Mal und notieren Sie den Durchschnittswert. - Wiederholen Sie Schritt 1.2 mit Block B.
- Block A über den Tisch mit einer konstanten Geschwindigkeit zu ziehen. Wenn die Geschwindigkeit konstant ist, sollte dann die Kraft auf die Waage zu lesen die Reibungskraft entsprechen. Berechnen
 für Block A. Tun Sie dies fünf Mal und notieren Sie den Durchschnittswert.
für Block A. Tun Sie dies fünf Mal und notieren Sie den Durchschnittswert. - Wiederholen Sie Schritt 1.4 mit Block B.
(2) Effekt von Gewicht auf die Kraft der Reibung.
- Platz Block A auf Block B und wiederholen Sie Schritt 1.4 fünf Mal, den durchschnittlichen Wert zu bestimmen. Berechnen des Faktors, mit dem die Reibungs erhöht/verringert Kraft.
- Platz Block B auf Block A und wiederholen Sie Schritt 1.4 fünfmal, Bestimmung des Durchschnittswerts. Berechnen des Faktors, mit dem die Reibungs erhöht/verringert Kraft.
3. Auswirkungen der Fläche auf Kraft der Reibung.
- Drehen Sie Block B auf der Seite, die nur den Rand der Pfanne enthält. Das Gewicht muss oben auf der Seite nach oben gelegt werden. Messen Sie die Kraft der Reibung zu und vergleichen Sie es mit der in Schritt 1.2 gemessene Wert. Berechnen des Faktors, mit dem die Reibungs erhöht/verringert Kraft.
4. Winkel von Ruhe.
- Block A auf der verstellbaren schiefen Ebene, ab einem Winkel von 0° zu platzieren. Heben Sie langsam den Winkel, bis der Block beginnt zu rutschen. Mit einem Winkelmesser, Messen Sie den Winkel des Ausruhens und mit Gleichung 3 berechnen der Koeffizient der statischen Friktion, kurz bevor der Block anfing zu rutschen. Tun Sie dies fünf Mal und notieren Sie den Durchschnittswert.
- Wiederholen Sie Schritt 4.2 mit Block B.
Ergebnisse
Tabelle 1. Reibungskoeffizienten.
| Block | 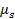 |
 |
| A | 0,68 | 0,60 |
| B | 0,52 | 0,47 |
Tabelle 2. Wirkung von Gewicht und Oberfläche auf die Kraft der Reibung.
| Messung | 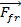 (N) |
Faktor, mit dem es größer oder kleiner ist |
| Block B auf A | 16 | Mit 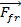 Schritt von 1,4 = 2,3 Schritt von 1,4 = 2,3 |
| Block A auf B | 14 | Mit 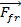 aus Schritt 1.5 = 2,5 aus Schritt 1.5 = 2,5 |
| Kleine Fläche | 5 | Mit 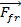 Schritt von 1,4 = 0,9 Schritt von 1,4 = 0,9 |
Tabelle 3. Winkel von Ruhe.
| Block | Winkel von Ruhe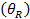 (°) |
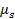 |
| A | 30 | 0,58 |
| B | 24 | 0,45 |
Die Ergebnisse des Experiments entsprechen die Vorhersagen von Gleichungen 1 und 2. In Schritt 1 war die Haftreibung größer als die kinetische Reibung. Dies ist immer dann der Fall, da mehr Kraft erforderlich ist, um die Reibung zu überwinden, wenn ein Objekt nicht bereits in Bewegung ist. In Schritt 2 bestätigte sich, dass die Kraft der Reibung proportional zu dem Gewicht der beiden Blöcke und der Koeffizient der kinetischen Friktion des Blocks in Kontakt mit dem Tisch war. Das Ergebnis von Schritt 3 bestätigt, dass die Fläche nicht die Kraft der Reibung beeinflusst. In Schritt 4 kann der Winkel der Ruhe durch Gleichung 3angenähert werden. Der Fehler in Verbindung mit dem Lab kommt von der Schwierigkeit des Lesens der Kraft-Skala unter Beibehaltung einer konstanten Geschwindigkeit für den Gleitstein. Durch mehrere Messungen und Berechnung des Durchschnitts, kann dieser Effekt reduziert werden.
Anwendung und Zusammenfassung
Reibung ist überall in unserem täglichen Leben. In der Tat wäre es nicht möglich, ohne es zu gehen. Wenn jemand versucht, zu Fuß auf einer glatten Oberfläche, würde er nirgendwo gehen. Es ist nur die Reibung zwischen der Unterseite seiner Füße und den Boden als seine Muskeln drücken gegen den Boden, der ihn vorwärts treibt.
In fast jedem Aspekt der Industrie versuchen Ingenieure, die Reibung zu reduzieren. Wenn zwei Flächen in Kontakt stehen, werden immer Reibung. Dies nehmen die Form von Wärme, wie die Hitze spüren, wenn jemand schnell ihre Hände zusammen reibt. In industriellen Anwendungen kann diese Wärme Maschinen beschädigen. Reibungskräfte auch gegen die Bewegung von Objekten und fertig mechanische Vorgänge verlangsamen können. Daher sind Substanzen wie Schmiermittel verwendet, um den Reibwert zwischen zwei Flächen zu verringern.
Tabelle 4. Reibungskoeffizienten Beispiel.
| Materialien |  |
| Holz auf Holz | 0,2 |
| Messing auf Stahl | 0,44 |
| Kautschuk auf Beton | 0,8 |
| geschmierten Kugellagern | < 0,01 |
In diesem Experiment wurden die Koeffizienten der statische und kinetische Reibung für zwei verschiedene Holztäfelchen gemessen. Die Wirkung der Masse auf die Kraft der Reibung wurde zusammen mit der Wirkung der Fläche untersucht. Zu guter Letzt wurde der Winkel der Ruhe für einen Block auf einer schiefen Ebene gemessen.
Tags
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Reibung
Physics I
53.1K Ansichten

Newtonsche Gesetze der Bewegung
Physics I
76.9K Ansichten

Kraft und Beschleunigung
Physics I
79.7K Ansichten

Vektoren in mehrere Richtungen
Physics I
182.8K Ansichten

Kinematik und Projektilbewegung
Physics I
73.1K Ansichten

Newtonsches Gravitationsgesetz
Physics I
192.8K Ansichten

Der Impulserhaltung
Physics I
43.6K Ansichten

Hookesches Gesetz und harmonische Schwingungen
Physics I
61.6K Ansichten

Gleichgewichts- und Freikörper-Diagramme
Physics I
37.6K Ansichten

Drehmoment
Physics I
26.2K Ansichten

Rotationsträgheit
Physics I
43.8K Ansichten

Drehimpuls
Physics I
36.6K Ansichten

Energie und Arbeit
Physics I
50.4K Ansichten

Enthalpie
Physics I
60.6K Ansichten

Entropie
Physics I
17.8K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten