Atrito

Fonte: Nicholas Timmons, Asantha Cooray, PhD, Departamento de Física & Astronomia, Escola de Ciências Físicas, Universidade da Califórnia, Irvine, CA

O objetivo deste experimento é examinar a natureza física dos dois tipos de atrito (ou seja, estática e cinética). O procedimento incluirá a medição dos coeficientes de atrito para objetos deslizando horizontalmente, bem como para baixo de um plano inclinado.

O atrito não é completamente compreendido, mas é experimentalmente determinado ser proporcional à força normal exercida sobre um objeto. Se um microscópio se aproximar de duas superfícies que estão em contato, revelaria que suas superfícies são muito ásperas em pequena escala. Isso evita que as superfícies deslizem facilmente umas pelas outras. A combinação do efeito de superfícies ásperas com as forças elétricas entre os átomos nos materiais pode explicar a força de atrito.

Há dois tipos de atrito. O atrito estático está presente quando um objeto não está se movendo e alguma força é necessária para colocar esse objeto em movimento. O atrito cinético está presente quando um objeto já está se movendo, mas diminui a velocidade devido ao atrito entre as superfícies deslizantes.

Figura 1.

A Figura 1 mostra quatro forças agindo em um objeto que se senta em um plano horizontal. 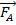corresponde a alguma força horizontal aplicada. é a força da gravidade no objeto, que é combinada igualmente, mas na direção oposta pela força normal, 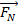. A força normal é o resultado de uma superfície agindo sobre um objeto em oposição à gravidade. A força normal explica por que um livro não simplesmente cai na mesa em que está descansando. Finalmente, oposição à força aplicada é a força de atrito, 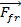. A força de atrito é proporcional à força normal:

, (Equação 1)

onde está o coeficiente do atrito.

O coeficiente de atrito deve ser medido experimentalmente e é uma propriedade que depende dos dois materiais que estão em contato. Existem dois tipos de coeficientes de atrito: atrito cinético, quando os objetos já estão em movimento, e atrito estático, 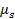quando os objetos estão em repouso e requerem uma certa quantidade de força para se mover. Para um objeto deslizando ao longo de um caminho, a força normal é igual ao peso do objeto. Portanto, a força de atrito depende apenas do coeficiente e da massa de um objeto.

Se o objeto estiver em um plano inclinado, então a força normal 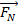é perpendicular à inclinação e não é igual e oposta ao peso, como pode ser visto na Figura 2.

Figura 2.

Neste caso, apenas um componente é equivalente à força normal, dependendo do ângulo φ:

. (Equação 2)

O ângulo de repouso 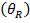é definido como o ponto em que a força da gravidade em um objeto supera a força de atrito estática e o objeto começa a deslizar por um plano inclinado. Uma boa aproximação para o ângulo do repouso é:

. (Equação 3)

Neste laboratório, duas panelas metálicas serão usadas para representar materiais com diferentes coeficientes de atrito. O bloco A terá um fundo de papel de areia, o que resultará em um coeficiente mais alto de atrito, enquanto o bloco B terá um fundo metálico liso.

1. Meça os coeficientes de atrito.

1. Adicione um peso de 1.000 g a cada bloco e use uma medida de escala para as massas dos blocos A e B, incluindo a massa adicionada.
2. Conecte a escala de força ao bloco A. Puxe a balança horizontalmente e observe a leitura pouco antes do bloco começar a deslizar. Pouco antes de começar a deslizar, a quantidade máxima de atrito estático está resistindo ao movimento. Use a leitura de força para calcular 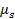para o bloco A. Faça isso cinco vezes e regise o valor médio.
3. Repita o passo 1.2 com o bloco B.
4. Puxe o bloco A através da mesa em uma velocidade constante. Se a velocidade é constante, então a leitura de força na escala deve ser igual à força de atrito. Calcule para o bloco A. Faça isso cinco vezes e regise o valor médio.
5. Repita o passo 1.4 com o bloco B.

2. Efeito do peso sobre a força do atrito.

1. Coloque o bloco A na parte superior do bloco B e repita o passo 1,4 cinco vezes, determinando o valor médio. Calcule o fator pelo qual a força de fricção aumentou/diminuiu.
2. Coloque o bloco B em cima do bloco A e repita o passo 1,4 cinco vezes, determinando o valor médio. Calcule o fator pelo qual a força de fricção aumentou/diminuiu.

3. Efeito da área de superfície sobre a força de atrito.

1. Gire o bloco B para o lado que contém apenas a borda da panela. O peso precisará ser colocado na parte superior do lado para cima. Meça a força do atrito e compare-a com o valor medido na etapa 1.2. Calcule o fator pelo qual a força de fricção aumentou/diminuiu.

4. Ângulo de repouso.

1. Coloque o bloco A no plano inclinado ajustável, começando em um ângulo de 0°. Levante lentamente o ângulo até que o bloco comece a deslizar. Usando um prolongador, meça o ângulo de repouso e use a Equação 3 para calcular o coeficiente de atrito estático pouco antes do bloco começar a deslizar. Faça isso cinco vezes e regise o valor médio.
2. Repita o passo 4.2 com o bloco B.

 Mesa 1. Coeficientes de atrito.

Bloquear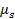
Um	0.68	0.60
B	0.52	0.47

Mesa 2. Efeito do peso e da área da superfície na força do atrito.

Medição	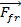(N)	Fator pelo qual é maior ou menor
Bloco B em A	16	Com 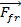a partir do passo 1.4 = 2,3
Bloco A em B	14	Com 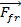a partir do passo 1.5 = 2,5
Pequena área de superfície	5	Com 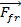a partir do passo 1.4 = 0,9

Mesa 3. Ângulo de repouso.

Bloquear	Ângulo de repouso (°)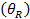
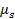Um	30	0.58
B	24	0.45

Os resultados obtidos a partir do experimento correspondem às previsões feitas pelas Equações 1 e 2. Na etapa 1, o atrito estático foi maior do que o atrito cinético. Este é sempre o caso, pois mais força é necessária para superar o atrito quando um objeto ainda não está em movimento. Na etapa 2, foi confirmado que a força de atrito era proporcional ao peso de ambos os blocos e ao coeficiente de atrito cinético do bloco em contato com a tabela. O resultado da etapa 3 confirma que a área da superfície não afeta a força de atrito. Na etapa 4, o ângulo do repouso pode ser aproximado pela Equação 3. O erro associado ao laboratório vem da dificuldade de leitura da escala de força, mantendo uma velocidade constante para o bloco deslizante. Ao tomar várias medidas e calcular a média, esse efeito pode ser reduzido.

O atrito está em toda parte em nossas vidas diárias. Na verdade, não seria possível andar sem ele. Se alguém tentasse andar em uma superfície sem atrito, ele não iria a lugar nenhum. É apenas o atrito entre a parte inferior de seus pés e o chão como seus músculos empurram contra o chão que o impulsiona para a frente.

Em quase todos os aspectos da indústria, os engenheiros estão tentando reduzir o atrito. Quando duas superfícies estiverem em contato, sempre haverá atrito. Isso pode tomar a forma de calor, como o calor sentido quando alguém rapidamente esfrega as mãos juntas. Em aplicações industriais, esse calor pode danificar as máquinas. As forças de atrito também se opõem ao movimento dos objetos e podem retardar as operações mecânicas feitas. Portanto, substâncias como lubrificantes são utilizadas para diminuir o coeficiente de atrito entre duas superfícies.

Mesa 4. Exemplos de atrito.

Materiais
madeira na madeira	0.2
latão em aço	0.44
borracha no concreto	0.8
rolamentos de esferas lubrificados	< 0,01

Neste experimento, os coeficientes de atrito estático e cinético foram medidos para dois blocos deslizantes diferentes. O efeito da massa sobre a força do atrito foi examinado, juntamente com o efeito da área de superfície. Por último, o ângulo de repouso de um bloco em um plano inclinado foi medido.