Redes de tubulação e perdas de pressão
Visão Geral
Fonte: Alexander S Rattner, Departamento de Engenharia Mecânica e Nuclear, Universidade Estadual da Pensilvânia, University Park, PA
Este experimento introduz a medição e modelagem de perdas de pressão em redes de tubulação e sistemas de fluxo interno. Nesses sistemas, a resistência ao fluxo de atrito das paredes do canal, conexões e obstruções faz com que a energia mecânica na forma de pressão de fluido seja convertida em calor. Análises de engenharia são necessárias para dimensionar o hardware de fluxo para garantir perdas aceitáveis de pressão de atrito e selecionar bombas que atendam aos requisitos de queda de pressão.
Neste experimento, uma rede de tubulação é construída com características comuns de fluxo: comprimentos retos de tubulação, bobinas de tubo helicoidal e encaixes de cotovelo (curvas afiadas de 90°). As medidas de perda de pressão são coletadas em cada conjunto de componentes usando manômetros - dispositivos simples que medem a pressão do fluido pelo nível líquido em uma coluna vertical aberta. As curvas de perda de pressão resultantes são comparadas com as previsões dos modelos de fluxo interno.
Princípios
Quando o fluido flui através de canais fechados (por exemplo,tubos, tubos, vasos sanguíneos) deve superar a resistência de atrito das paredes do canal. Isso causa uma perda contínua de pressão na direção do fluxo à medida que a energia mecânica é convertida em calor. Este experimento concentra-se na medição e modelagem de tais perdas de pressão em sistemas de fluxo interno.
Para medir a queda de pressão ao longo dos canais, este experimento usará o princípio da variação da pressão hidrostática. No fluido estacionário, a pressão só varia com profundidade devido ao peso do fluido (Eqn. 1, Fig. 1a).
 (1)
(1)
Aqui 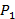 e estão as
e estão as  pressões em dois pontos, ρ é a densidade do fluido, g é a aceleração gravitacional, e h1 e h2 são as profundidades (medidas na direção da gravidade) dos pontos a partir de um nível de referência. Em condições ambientais típicas, a densidade da água é de 998 kgm -3 e a densidade do ar é de 5a = 1,15 kg m-3. Como ρa << ρw, variações de pressão hidrostática no ar podem ser negligenciadas em comparação com variações de pressão hidrostática líquida, e a pressão atmosférica ambiente pode ser assumida uniforme(Patm ~ 101 kPa). Seguindo este princípio, a queda de pressão ao longo de um fluxo de canal pode ser medida pela diferença nos níveis de fluido em tubos verticais abertos ligados ao canal:
pressões em dois pontos, ρ é a densidade do fluido, g é a aceleração gravitacional, e h1 e h2 são as profundidades (medidas na direção da gravidade) dos pontos a partir de um nível de referência. Em condições ambientais típicas, a densidade da água é de 998 kgm -3 e a densidade do ar é de 5a = 1,15 kg m-3. Como ρa << ρw, variações de pressão hidrostática no ar podem ser negligenciadas em comparação com variações de pressão hidrostática líquida, e a pressão atmosférica ambiente pode ser assumida uniforme(Patm ~ 101 kPa). Seguindo este princípio, a queda de pressão ao longo de um fluxo de canal pode ser medida pela diferença nos níveis de fluido em tubos verticais abertos ligados ao canal:  (Fig. 1b). Esses dispositivos de medição de pressão baseados em nível líquido são chamados de manômetros.
(Fig. 1b). Esses dispositivos de medição de pressão baseados em nível líquido são chamados de manômetros.
A perda de pressão ao longo de um comprimento de um canal pode ser prevista com a fórmula do fator de atrito Darcy (Eqn. 2). Aqui, 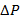 está a perda de pressão ao longo de um comprimento(L) de canal com diâmetro interno D. U é a velocidade média do canal, definida como a taxa de fluxo de volume de fluido (por exemplo,em m3 s-1) dividida pela área transversal do canal(por exemplo,em m2,
está a perda de pressão ao longo de um comprimento(L) de canal com diâmetro interno D. U é a velocidade média do canal, definida como a taxa de fluxo de volume de fluido (por exemplo,em m3 s-1) dividida pela área transversal do canal(por exemplo,em m2,  para canais circulares). f é o fator de atrito Darcy, que segue diferentes tendências para diferentes geometrias de canais e taxas de fluxo. Neste experimento, os fatores de atrito serão medidos experimentalmente para comprimentos retos e helicoicamente enrolados do tubo, e comparados com fórmulas publicadas anteriormente.
para canais circulares). f é o fator de atrito Darcy, que segue diferentes tendências para diferentes geometrias de canais e taxas de fluxo. Neste experimento, os fatores de atrito serão medidos experimentalmente para comprimentos retos e helicoicamente enrolados do tubo, e comparados com fórmulas publicadas anteriormente.
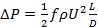 (2)
(2)
As tendências do fator de atrito do fluxo de canal dependem do número de Reynolds (Re), que mede a força relativa dos efeitos da inércia do fluido aos efeitos da viscosidade fluida (efeitos de atrito). Re é definido como  , onde é a
, onde é a  viscosidade dinâmica do fluido (~0,001 kg m-1 s-1 para água em condições ambientais). No baixo Re (
viscosidade dinâmica do fluido (~0,001 kg m-1 s-1 para água em condições ambientais). No baixo Re ( 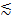 2000 em canais retos), efeitos viscosos são fortes o suficiente para amortecer redemoinhos no fluxo, levando a um fluxo suave de laminar. No higher Re
2000 em canais retos), efeitos viscosos são fortes o suficiente para amortecer redemoinhos no fluxo, levando a um fluxo suave de laminar. No higher Re  (2000), redemoinhos aleatórios podem se formar no fluxo, levando a comportamentos turbulentos. Modelos de fator de atrito comumente utilizados para fluxos de canais circulares retos são apresentados em Eqn. 3.
(2000), redemoinhos aleatórios podem se formar no fluxo, levando a comportamentos turbulentos. Modelos de fator de atrito comumente utilizados para fluxos de canais circulares retos são apresentados em Eqn. 3.
 (3)
(3)
Quando o fluido flui através de bobinas de tubo helicoidal, formam vórtices internos secundários (Fig. 1c). Como resultado, o fator de atrito  também depende do número do Reitor, que explica a influência relativa da curvatura do tubo:
também depende do número do Reitor, que explica a influência relativa da curvatura do tubo:  . Aqui R é o raio da bobina do tubo, medido do eixo central até a metade da tubulação. Uma correlação comum para
. Aqui R é o raio da bobina do tubo, medido do eixo central até a metade da tubulação. Uma correlação comum para  é:
é:
 (4)
(4)
Os encaixes do tubo, válvulas, expansões/contrações e outras obstruções também causam perdas de pressão. Uma abordagem para modelar tais pequenas perdas é em termos do comprimento equivalente de canal simples necessário para produzir a mesma queda de pressão(Le/D). Aqui,  e estão o fator de atrito e a velocidade de fluxo nos
e estão o fator de atrito e a velocidade de fluxo nos 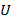 comprimentos da entrada/canal de saída (Fig 1d).
comprimentos da entrada/canal de saída (Fig 1d).
 (5)
(5)
Tabelas de comprimentos de canal equivalentes representativos são relatadas em manuais para componentes de encanamento comuns(c.f., [1]). Este experimento irá medir os comprimentos equivalentes para encaixes afiados de 90°bend (cotovelos). Os comprimentos equivalentes típicos relatados para tais encaixes são Le/D ~ 30.
Procedimento
1. Fabricação do sistema de tubulação (ver esquema e fotografia, Fig. 2)
- Afixar (fita ou cola) um pequeno reservatório de água plástica à superfície de trabalho. Se for um recipiente coberto, faça furos na tampa para as linhas de água de entrada e saída e cabo de alimentação da bomba.
- Monte a pequena bomba submersível no reservatório.
- Monte o rotametro (medidor de fluxo de água) verticalmente na área de trabalho. Pode ajudar a amarrar o rotametro a um pequeno feixe vertical ou suporte L para mantê-lo ereto. Conecte um tubo de fluxo da saída da bomba à entrada do rotametro (porta inferior).
- Conecte tees de encaixe de compressão plástica às duas extremidades de uma seção de tubo plástico rígido (recomendo comprimento L ~ 0,3 m, diâmetro interno do tubo D ~ 6,4 mm). Monte as tees nos grampos do tubo. Conecte a tubulação de borracha de uma camiseta (entrada) à saída do rotametro. Conecte tubos de borracha do outro tee (saída) ao reservatório.
- Construa um segundo conjunto com dois encaixes de tee montados. Enrole um comprimento de tubos de plástico macio enrolados helicamente em torno de um núcleo cilíndrico (recomendo tubo de papelão, R ~ 30 mm e ~5 envoltórios de tubo). As amarras ou grampos podem ajudar a manter o tubo enrolado. Instale as duas extremidades livres da tubulação nos encaixes do tee.
- Construa um terceiro conjunto com dois encaixes de tee montados. Conecte quatro (ou mais) cotovelos com comprimentos curtos de tubo plástico rígido entre as tees. O uso de vários cotovelos amplifica a leitura da queda de pressão, melhorando a precisão da medição.
- Instale tubos plásticos rígidos claros (~0,6 m) nas portas abertas nos encaixes de seis tees. Use um nível para garantir que os tubos sejam verticais. Estes tubos serão os manômetros (dispositivos de medição de pressão).
- Encha o reservatório com água.
2. Operação
- Tubo reto: Ligue a bomba e ajuste a válvula rotamétrica para variar as taxas de fluxo de água. Para cada caso, registo da vazão da água e do nível vertical da água em cada tubo de manômetro. Regissuor a queda de pressão com base na diferença nos níveis de manômetro (Eqn. 1).
- Tubo enrolado: Conecte a entrada da seção de teste enrolada à saída do rotametro e a saída da seção de teste ao reservatório. Como no Passo 2.1, registo da vazão de água e queda de pressão para uma série de taxas de fluxo.
- Encaixes de cotovelo: Conecte a seção de teste de encaixe do cotovelo ao rotador e ao reservatório. Colete um conjunto de medidas de fluxo e pressão, como na Etapa 2.2.
3. Análise
- Para a caixa do tubo reto, avalie o número de Reynolds e o fator de atrito f (Eqn. 2). Avalie as incertezas do número de Reynolds e do fator de atrito (Eqn. 6). Aqui eΔP é a incerteza nas medidas de pressão (
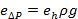 , é a incerteza no nível do
, é a incerteza no nível do  manômetro), e eU é a incerteza na velocidade média do canal (da folha de dados do rotametro, com incerteza típica de 3 a 5% do alcance). Para água em temperatura ambiente (22°C), ρ = 998 kg m-3 e μ = 0,001 kg m-1 s-1.
manômetro), e eU é a incerteza na velocidade média do canal (da folha de dados do rotametro, com incerteza típica de 3 a 5% do alcance). Para água em temperatura ambiente (22°C), ρ = 998 kg m-3 e μ = 0,001 kg m-1 s-1.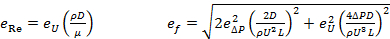 (6)
(6) - Compare os resultados do fator de atrito da Etapa 3.1 com os modelos analíticos (Eqn. 3).
- Repita o passo 3.1 para a caixa do tubo enrolado. Desta vez, subtraia a queda de pressão prevista (Eqns. 2-3) para a parte reta da seção de teste de ΔP. Aqui assumimos que a incerteza na correção da pressão em linha reta é insignificante. Compare fatores de atrito medidos com valores da correlação (Eqn. 4).
- Repita o passo 3.2 para a caixa de encaixe do cotovelo. Subtraia a queda de pressão prevista para os comprimentos retos da tubulação entre os encaixes do cotovelo para obter uma perda de pressão corrigida
 . Avalie o comprimento equivalente e a incerteza para cada cotovelo. Aqui, Ne é o número de cotovelos de cano.
. Avalie o comprimento equivalente e a incerteza para cada cotovelo. Aqui, Ne é o número de cotovelos de cano. (7)
(7) - Compare o resultado de comprimento equivalente(Le/D) com os valores típicos relatados (~30).
Resultados
Fator de atrito medido e dados de comprimento equivalente são apresentados em Fig. 3a-c. Para a seção do tubo reto, é utilizado um tubo de PVC claro com D = 6,4 mm e L = 284 mm. As taxas de fluxo medidos (0,75 - 2,10 l min-1) correspondem a condições turbulentas (Re = 2600 - 7300). Fatores de atrito correspondem às previsões do modelo analítico à incerteza experimental. A incerteza f relativamente alta é encontrada em baixas taxas de fluxo devido à precisão limitada do medidor de fluxo selecionado (de baixo custo) (± 0,15 l min-1).
Os resultados do fator de atrito para o caso da bobina do tubo também correspondem à correlação fornecida (Eqn. 4) dentro da incerteza experimental (Fig. 3b). São utilizadas cinco ciclos de bobina do raio R = 33 mm com diâmetro interno do tubo D = 6,4 mm. Aqui, o número do Reitor é 500 - 5600, que corresponde à porção laminar de Eqn. 4. Os fatores de atrito medidos são significativamente mais elevados do que para a seção reta a taxas de fluxo iguais. Isso decorre do efeito estabilizador da geometria do tubo da bobina, que atrasa a transição para a turbulência para a re alta.
Para a caixa do cotovelo, são empregados 4 encaixes de cotovelo (número de peça na lista de materiais), conectados por comprimentos curtos de D = tubos de 6,4 mm. O comprimento de atrito equivalente de cada encaixe do cotovelo se aproxima(Le/D) ~ 30 - 40 em re alto (Fig. 3c). Isso é semelhante a um valor comumente relatado de 30. Observe que a resistência de atrito real é específica para a geometria de montagem, e os valores Le/Drelatados só devem ser considerados como diretrizes.
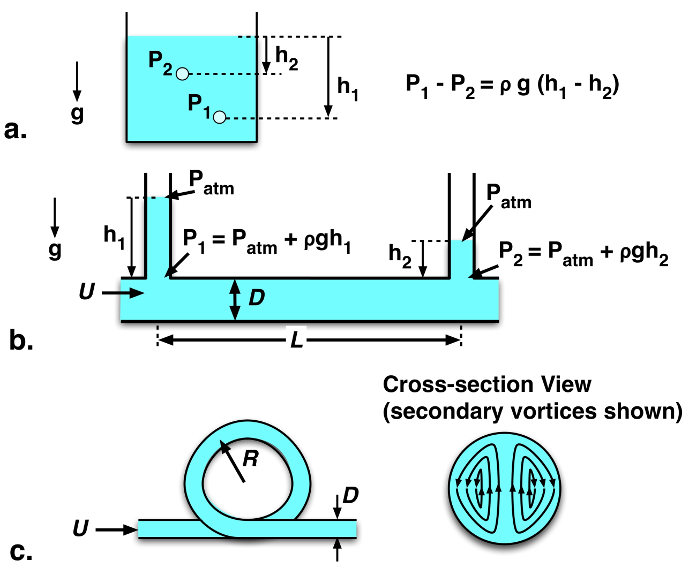
Figura 1: a. Esquema de variação de pressão hidrostática em um corpo estacionário de fluido. b. Mudança de pressão ao longo de um comprimento reto do tubo, medido com manômetros abertos. c. Esquema de tubo enrolado, com vórtices internos indicados na visão transversal.
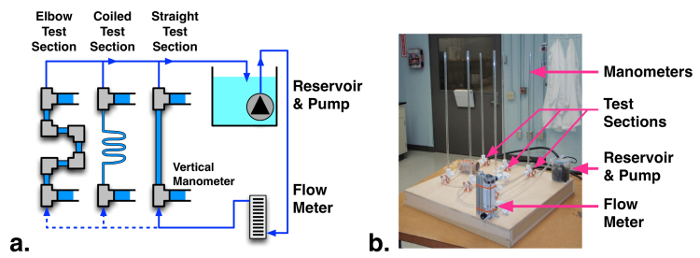
Figura 2: (a) Fotografia esquemática e (b)da instalação de medição de queda de pressão. Clique aqui para ver uma versão maior desta figura.

Figura 3: Fator de atrito e medidas de comprimento equivalentes e previsões de modelo para: a. Tubo reto, b. Tubo enrolado, c. Encaixes de cotovelo.
Aplicação e Resumo
Resumo
Este experimento demonstra métodos para medir fatores de atrito de queda de pressão e comprimentos equivalentes em redes de fluxo interno. Métodos de modelagem são apresentados para configurações comuns de fluxo, incluindo tubos retos, tubos enrolados e encaixes de tubulação. Essas técnicas experimentais e de análise são ferramentas-chave de engenharia para o projeto de sistemas de fluxo de fluidos.
Aplicativos
Redes de fluxo interno surgem em inúmeras aplicações, incluindo usinas de geração de energia, processamento químico, distribuição de fluxo dentro de trocadores de calor e circulação sanguínea em organismos. Em todos os casos, é fundamental poder prever e modelar perdas de pressão e requisitos de bombeamento. Esses sistemas de fluxo podem ser decompostos em seções de canais retos e curvados, conectados por encaixes ou junções. Aplicando fator de atrito e modelos de perda menor a esses componentes, descrições de rede inteiras podem ser formuladas.
Lista de Materiais
| Nome | Companhia | Número do catálogo | Comentários |
| Equipamento | |||
| Bomba de água submersível | Uniclife | B018726M9K | |
| Recipiente plástico coberto | Reservatório de água, recipiente de alimentos plásticos utilizado neste estudo. | ||
| Medidor de fluxo de água | UXCell | LZM-15 | Rotameter, 0,5 – 4.0 l min-1 |
| Tubo de PVC claro rígido | Mcmaster | 53945K13 | Para seções de teste e manômetros, 1/4" ID, 3/8" OD |
| Tubo de PVC macio flexível | Mcmaster | 5233K63
5233K56 |
Para conexões de tubulação e seção de teste de bobina |
| Encaixe do tubo plástico | Mcmaster | 5016K744 | Para seções de teste entrada e conexões de saída/manômetros |
| Cotovelo de encaixe do tubo plástico | Mcmaster | 5016K133 | Para seção de teste com cotovelos |
Pular para...
Vídeos desta coleção:

Now Playing
Redes de tubulação e perdas de pressão
Mechanical Engineering
58.7K Visualizações

Empuxo e Arrasto em Corpos Imersos
Mechanical Engineering
30.2K Visualizações

Estabilidade de Embarcações Flutuantes
Mechanical Engineering
23.1K Visualizações

Propulsão e Impulso
Mechanical Engineering
22.1K Visualizações

Resfriamento e Ebulição
Mechanical Engineering
8.2K Visualizações

Saltos Hidráulicos
Mechanical Engineering
41.3K Visualizações

Análise de Trocadores de Calor
Mechanical Engineering
28.3K Visualizações

Introdução à Refrigeração
Mechanical Engineering
25.0K Visualizações

Anemometria com fio quente
Mechanical Engineering
15.8K Visualizações

Medindo fluxos turbulentos
Mechanical Engineering
13.6K Visualizações

Visualização do Fluxo ao Redor de um Corpo Parado
Mechanical Engineering
12.1K Visualizações

Jato Incidindo em uma Placa Inclinada
Mechanical Engineering
10.8K Visualizações

Abordagem de Conservação de Energia para Análise de Sistemas
Mechanical Engineering
7.4K Visualizações

Conservação de Massa e Medições de Taxa de Fluxo
Mechanical Engineering
22.9K Visualizações

Determinação das Forças de Impacto em uma Placa Plana com o Método do Volume de Controle
Mechanical Engineering
26.0K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados