Misurazione di flussi turbolenti
Panoramica
Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Dipartimento di Ingegneria Meccanica, Michigan State University, East Lansing, MI
I flussi turbolenti mostrano fluttuazioni di frequenza molto elevate che richiedono strumenti ad alta risoluzione temporale per la loro appropriata caratterizzazione. Gli anemometri a filo caldo hanno una risposta temporale abbastanza breve per soddisfare questo requisito. Lo scopo di questo esperimento è dimostrare l'uso dell'anemometria a filo caldo per caratterizzare un getto turbolento.
In questo esperimento, una sonda a filo caldo precedentemente calibrata verrà utilizzata per ottenere misurazioni della velocità in diverse posizioni all'interno del getto. Infine, dimostreremo un'analisi statistica di base dei dati per caratterizzare il campo turbolento.
Principi
Descrizione di un flusso turbolento
Un flusso turbolento può essere evidenziato da fluttuazioni altamente casuali nelle variabili di flusso come velocità, pressione e vorticità. La Figura 1 rappresenta un tipico segnale di velocità ottenuto misurando la velocità in un punto fisso in un flusso turbolento. Le fluttuazioni in questo segnale non sono rumore casuale, ma il risultato di interazioni non lineari tra movimenti coerenti all'interno del campo di flusso. Una descrizione classica del flusso turbolento, comporta la determinazione del valore medio delle variabili di flusso e delle loro corrispondenti fluttuazioni con il passare del tempo. A tal fine, usiamo la definizione per la media di una funzione per determinare la media di una misurazione della velocità:
 (1)
(1)
Ecco 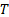 la dimensione del dominio di integrazione, che sarà un intervallo di tempo nelle misurazioni presenti. Come suggerito dall'equazione (1), useremo una barra superiore per indicare la media di una variabile. Dato che un'acquisizione digitale di un segnale è discreta, l'integrale nell'equazione (1) dovrebbe essere risolto numericamente, usando la regola trapezoidale o la regola di Simpson [1]. Le fluttuazioni di una variabile dipendente dal tempo
la dimensione del dominio di integrazione, che sarà un intervallo di tempo nelle misurazioni presenti. Come suggerito dall'equazione (1), useremo una barra superiore per indicare la media di una variabile. Dato che un'acquisizione digitale di un segnale è discreta, l'integrale nell'equazione (1) dovrebbe essere risolto numericamente, usando la regola trapezoidale o la regola di Simpson [1]. Le fluttuazioni di una variabile dipendente dal tempo  come possono quindi essere calcolate come segue:
come possono quindi essere calcolate come segue:
 (2)
(2)
Come si vede in questa equazione, i campi di fluttuazione sono indicati da un simbolo primo. Applicando l'equazione (1) a  , possiamo facilmente determinare che la media di un campo di fluttuazione è zero:
, possiamo facilmente determinare che la media di un campo di fluttuazione è zero:
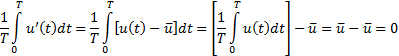 (3)
(3)
Quindi, un descrittore statistico più appropriato per il campo di fluttuazione è il quadrato medio radice delle fluttuazioni:
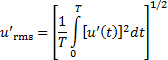 (4)
(4)
Questo descrittore statistico è infatti una misura molto comune dell'intensità della turbolenza. L'attuale esperimento si baserà sulla determinazione della velocità media e dell'intensità di turbolenza di un campo turbolento.
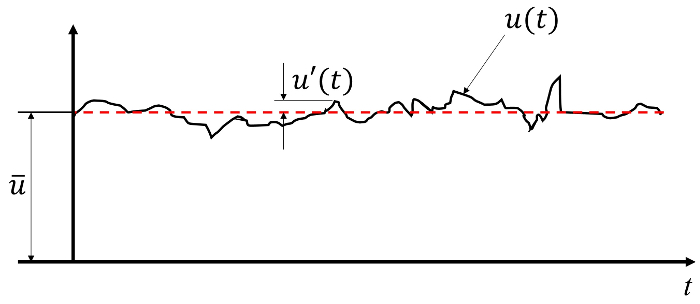
Figura 1. Tipico segnale di velocità di un flusso turbolento come recuperato da un anemometro a filo caldo. Il segnale  grezzo, , può essere scomposto in un campo di fluttuazione,
grezzo, , può essere scomposto in un campo di fluttuazione, 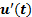 , sovrapposto al valore medio della velocità,
, sovrapposto al valore medio della velocità,  .
.
Configurazione sperimentale
Come mostrato nella Figura 2 (A) la struttura è fondamentalmente un plenum che viene pressurizzato da un ventilatore centrifugo. La figura 2 (B) mostra che c'è una fessura sul lato opposto del plenum che emette un getto planare. Come mostrato nella Figura 2 (C), un sistema di attraversamento tiene l'anemometro a filo caldo in posizioni prescritte nel getto planare. Questo sistema di attraversamento verrà utilizzato per determinare la velocità in diverse posizioni di interesse nel getto. Lo schema della Figura 3 mostra una posizione rappresentativa in cui verrà eseguita l'anemometria al fine di caratterizzare il campo turbolento nel getto planare.

Figura 2. Configurazione sperimentale. (A): impianto di flusso; il plenum è pressurizzato per mezzo di un ventilatore centrifugo. (B): fessura per l'emissione del getto planare. (C): sistema di attraversamento per modificare la posizione dell'anemometro lungo il getto. Fare clic qui per visualizzare una versione più grande di questa figura.

Figura 3. Schema del getto planare che mostra: la vena contracta, la distribuzione della velocità in una data posizione a valle e il diagramma delle connessioni. Clicca qui per visualizzare una versione più grande di questa figura.
Procedura
- Misurare la larghezza della fessura, W, e registrare questo valore nella tabella 1.
- Impostare l'anemometro a filo caldo a una distanza dall'uscita pari a x = 1,5W lungo l'asse di mezzeria. Registrare questa posizione in modo razionale nella tabella 2. L'asse di mezzeria è l'origine della coordinata spanwise (y = 0).
- Avviare il programma di acquisizione dati per attraversare il jet. Impostare la frequenza di campionamento a 500 Hz per un totale di 5000 campioni (cioè 10 secondi di dati).
- Registrare l'attuale posizione spanwise del filo caldo nella tabella 3.
- Acquisire dati.
- Il sistema di acquisizione dati calcolerà la velocità media e l'intensità di turbolenza di quel set di dati utilizzando le equazioni (1) e (4).
- Registrare questi due valori nella tabella 3.
- Spostare il filo di scelta rapida nella posizione successiva (positiva) spanwise
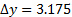 (mm).
(mm). - Ripetere i passaggi da 5 a 8 fino a quando non vi è alcun cambiamento evidente sia sulla velocità media che sull'intensità della turbolenza.
- Spostate di nuovo il cavo caldo sull'asse di mezzeria.
- Spostare il filo di scelta rapida nella posizione successiva (negativa) spanwise
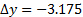 (mm).
(mm). - Acquisire dati.
- Il sistema di acquisizione dati calcolerà la velocità media e l'intensità di turbolenza di quel set di dati utilizzando le equazioni (1) e (4).
- Registrare questi due valori nella tabella 3.
- Ripetere i passaggi da 11 a 14 fino a quando non vi è alcun cambiamento evidente sia sulla velocità media che sull'intensità della turbolenza.
- Spostate il filo caldo di nuovo sull'asse di mezzeria del getto.
- Spostare il filo caldo lungo l'asse di mezzeria del getto nella direzione a valle in una nuova posizione (ad esempio x = 3W).
- Ripetere i passaggi da 4 a 17 per tutte le posizioni di flusso desiderate (ad esempio x = 1,5W, 3W, 6W, 9W).
Tabella 1 . Parametri di base per lo studio sperimentale.
| Parametro | Valore |
| Larghezza fessura (W) | 19,05 mm |
| Densitàdell'aria( r ) | 1,2 kg/m3 |
| Costante di calibrazione del trasduttore (m_p) | 76,75 Pa/V |
| Costante di calibrazione A | 5,40369 V2 |
| Costante di calibrazione B | 2,30234 V2(m/s)-0,65 |

Figura 4. Controllo del flusso nel sistema di flusso. La pila in cima al plenum serve allo scopo di deviare il flusso dalla fessura del getto permettendo di controllare la velocità di uscita del getto. Fare clic qui per visualizzare una versione più grande di questa figura.
Risultati
La Figura 5 mostra la distribuzione della velocità media attraverso il getto nella posizione a valle x = 3W. E la Figura 6 mostra la distribuzione dell'intensità della turbolenza attraverso il getto nella stessa posizione a valle. La tabella 3 ha i risultati per i valori locali della velocità media e dell'intensità di turbolenza nella posizione a flusso x = 3W. L'ultima colonna di questa tabella è il rapporto tra la velocità locale e la velocità della linea mediana. Questo rapporto viene utilizzato per determinare la larghezza del getto,  che è definita come la distanza tra le due posizioni in cui la velocità locale è il 50% della velocità della linea mediana. Si noti dalla tabella 2 che queste due posizioni si trovano da qualche parte negli intervalli
che è definita come la distanza tra le due posizioni in cui la velocità locale è il 50% della velocità della linea mediana. Si noti dalla tabella 2 che queste due posizioni si trovano da qualche parte negli intervalli 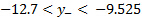 e
e 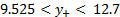 . Le loro posizioni esatte sono determinate utilizzando l'interpolazione lineare e sono determinate per essere:
. Le loro posizioni esatte sono determinate utilizzando l'interpolazione lineare e sono determinate per essere:  mm e
mm e  mm, per uno spessore del getto di
mm, per uno spessore del getto di 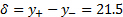 mm.
mm.
I risultati di quattro diversi esperimenti sono confrontati nella tabella 2. Questa tabella mostra come la velocità di mezzeria del getto,  , rimane sostanzialmente invariata per
, rimane sostanzialmente invariata per  , ma diminuisce con per
, ma diminuisce con per 
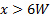 . Questo effetto è il risultato della presenza del nucleo potenziale per
. Questo effetto è il risultato della presenza del nucleo potenziale per 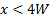 , e della sua scomparsa per
, e della sua scomparsa per  . Il nucleo potenziale è la regione all'interno del getto che non è stata influenzata dall'interazione tra l'ambiente e il getto. La regione di interazione è chiamata strato di miscelazione e cresce verso la linea mediana e lontano dal getto mentre il getto si muove a valle. Questa crescita è dovuta al trascinamento dell'aria circostante nel getto. A causa di questo effetto di trascinamento, il momento lineare del getto si diffonde nella direzione spanwise, causando l'aumento della sua larghezza con
. Il nucleo potenziale è la regione all'interno del getto che non è stata influenzata dall'interazione tra l'ambiente e il getto. La regione di interazione è chiamata strato di miscelazione e cresce verso la linea mediana e lontano dal getto mentre il getto si muove a valle. Questa crescita è dovuta al trascinamento dell'aria circostante nel getto. A causa di questo effetto di trascinamento, il momento lineare del getto si diffonde nella direzione spanwise, causando l'aumento della sua larghezza con  . Questo effetto è evidenziato dai risultati per
. Questo effetto è evidenziato dai risultati per  la tabella 2. A causa del fatto che la miscelazione avviene al confine tra il getto e l'ambiente circostante, l'intensità della turbolenza raggiunge picchi (
la tabella 2. A causa del fatto che la miscelazione avviene al confine tra il getto e l'ambiente circostante, l'intensità della turbolenza raggiunge picchi ( 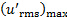 ) lontano dalla linea di mezzeria, in posizioni spanwise definite da
) lontano dalla linea di mezzeria, in posizioni spanwise definite da  e
e 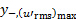 . Per semplicità, la Tabella 2 mostra solo i valori per il picco di intensità di turbolenza sul lato positivo del getto.
. Per semplicità, la Tabella 2 mostra solo i valori per il picco di intensità di turbolenza sul lato positivo del getto.

Figura 5. Risultati rappresentativi. Distribuzione della velocità a x = 3W.

Figura 6. Risultati rappresentativi. Distribuzione dell'intensità della turbolenza a x = 3W.
Tabella 2. Risultati rappresentativi. Diversi descrittori statistici per il getto planare a x = 1,5W, 3W, 6W e 9W.
| x/W | u ̅_cl (m/s) | δ (mm) | (u′_rms )_max (m/s) | y_(+,(u′_rms )_max ) |
| 1.5 | 27.677 | 19.37 | 4.919 | 0.9525 |
| 3.0 | 27.706 | 21.50 | 4.653 | 0.9525 |
| 6.0 | 24.783 | 28.18 | 4.609 | 0.9525 |
| 9.0 | 20.470 | 39.68 | 4.513 | 1.2700 |
Tabella 3. Risultati rappresentativi. Misure di velocità e intensità di turbolenza a x = 3W.
| y (mm) | u ̅ (m/s) | u′_rms (m/s) | u ̅∕u ̅_cl |
| -28.575 | 0.762 | 0.213 | 0.028 |
| -25.400 | 0.783 | 0.311 | 0.028 |
| -22.225 | 0.949 | 0.554 | 0.034 |
| -19.050 | 1.461 | 1.218 | 0.053 |
| -15.875 | 3.751 | 2.727 | 0.135 |
| -12.700 | 8.941 | 4.114 | 0.323 |
| -9.525 | 14.919 | 4.633 | 0.538 |
| -6.350 | 22.383 | 4.043 | 0.808 |
| -3.175 | 26.952 | 1.958 | 0.973 |
| 0.000 | 27.706 | 1.039 | 1.000 |
| 3.175 | 27.416 | 1.455 | 0.990 |
| 6.350 | 23.573 | 3.730 | 0.851 |
| 9.525 | 17.748 | 4.653 | 0.641 |
| 12.700 | 11.175 | 4.443 | 0.403 |
| 15.875 | 5.583 | 3.399 | 0.202 |
| 19.050 | 1.943 | 1.663 | 0.070 |
| 22.225 | 1.159 | 0.785 | 0.042 |
| 25.400 | 0.850 | 0.383 | 0.031 |
| 28.575 | 0.877 | 0.271 | 0.032 |
Applicazione e Riepilogo
Questo esperimento ha dimostrato l'applicazione dell'anemometria a filo caldo per caratterizzare i flussi turbolenti. Dato che la turbolenza presenta fluttuazioni di velocità ad alta frequenza, gli anemometri a filo caldo sono strumenti adatti per la sua caratterizzazione grazie alla loro elevata risoluzione temporale. Con questo in mente, abbiamo utilizzato un anemometro a filo caldo calibrato per caratterizzare la velocità locale media e l'intensità di turbolenza in diverse posizioni all'interno di un getto planare. Queste quantità sono state determinate utilizzando descrittori statistici per la turbolenza che sono stati spiegati nell'introduzione di questo documento. Da questi descrittori statistici, è stato osservato che il getto si diffonde nella direzione spanwise a causa del trascinamento del fluido, mentre i picchi di turbolenza all'interno degli strati di miscelazione, lontano dalla linea centrale del getto, come risultato della miscelazione del fluido.
Il flusso turbolento è onnipresente nelle applicazioni scientifiche e ingegneristiche. Per la sua valutazione in applicazioni ingegneristiche come ventilazione, riscaldamento e condizionamento dell'aria, è comune utilizzare sonde portatili a filo caldo che vengono introdotte nel condotto e attraversate radialmente per ottenere i profili di velocità. Queste informazioni vengono quindi utilizzate dall'ingegnere per bilanciare un sistema di flusso appena installato per garantirne il corretto funzionamento o per risolvere un sistema malfunzionante e risolvere qualsiasi problema che ne ostacoli il funzionamento.
Vai a...
Video da questa raccolta:

Now Playing
Misurazione di flussi turbolenti
Mechanical Engineering
13.6K Visualizzazioni

Galleggiabilità e trascinamento su corpi immersi
Mechanical Engineering
30.2K Visualizzazioni

Stabilità dei vasi galleggianti
Mechanical Engineering
23.3K Visualizzazioni

Propulsione e spinta
Mechanical Engineering
22.1K Visualizzazioni

Reti di tubazioni e perdite di carico
Mechanical Engineering
58.8K Visualizzazioni

Raffreddamento ed ebollizione
Mechanical Engineering
8.2K Visualizzazioni

Salti idraulici
Mechanical Engineering
41.3K Visualizzazioni

Analisi dello scambiatore di calore
Mechanical Engineering
28.3K Visualizzazioni

Introduzione alla refrigerazione
Mechanical Engineering
25.0K Visualizzazioni

Anemometria a filo caldo
Mechanical Engineering
15.9K Visualizzazioni

Visualizzazione del flusso oltre un corpo Bluff
Mechanical Engineering
12.2K Visualizzazioni

Getto che incide su una piastra inclinata
Mechanical Engineering
10.8K Visualizzazioni

Conservazione dell'energia come approccio all'analisi del sistema
Mechanical Engineering
7.4K Visualizzazioni

Conservazione di massa e misure di portata
Mechanical Engineering
23.0K Visualizzazioni

Determinazione delle forze di impingement su una piastra piana con il metodo del volume di controllo
Mechanical Engineering
26.0K Visualizzazioni