Applicazione della teoria dei gruppi nella spettroscopia infrarossa
Panoramica
Fonte: Tamara M. Powers, Dipartimento di Chimica, Texas A & M University
I complessi carbonilici metallici sono utilizzati come precursori metallici per la sintesi di complessi organometallici e catalizzatori. La spettroscopia infrarossa (IR) è uno dei metodi di caratterizzazione più utilizzati e informativi dei composti contenenti CO. La teoria dei gruppi, o l'uso della matematica per descrivere la simmetria di una molecola, fornisce un metodo per prevedere il numero di modalità vibrazionali C-O attive IR all'interno di una molecola. Osservare sperimentalmente il numero di allungamenti C-O nell'IR è un metodo diretto per stabilire la geometria e la struttura del complesso carbonilico metallico.
In questo video, sintetizzaremo il complesso carbonilico di molibdeno Mo(CO)4[P(OPh)3]2, che può esistere nelle forme cis- e trans-(Figura 1). Useremo la teoria dei gruppi e la spettroscopia IR per determinare quale isomero è isolato.
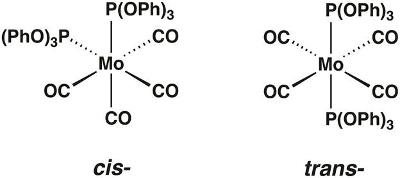
Figura 1. Gli isomeri cis- e trans-isomeri di Mo(CO)4[P(OPh)3]2.
Principi
Regole di selezione:
Le regole di selezione dettano il numero di transizioni elettroniche, da uno stato quantistico all'altro, che sono possibili per una data molecola. La spettroscopia IR sonda le transizioni vibrazionali dallo stato fondamentale della molecola, v = 0, al primo stato eccitato, v = 1. Il numero di gradi di libertà vibrazionale (normali modi di vibrazione) per molecole lineari e non lineari può essere calcolato utilizzando rispettivamente l'equazione 1 e l'equazione 2.
3N - 5 (1)
3N - 6 (2)
dove N = il numero di atomi nella molecola
Affinché una normale modalità di vibrazione sia attiva IR, il dipolo della molecola deve cambiare. Pertanto, tutte le normali modalità di vibrazione in cui non si verifica un cambiamento nel dipolo sono IR inattive. Il numero di modalità IR attive può essere determinato utilizzando la teoria dei gruppi.
Teoria deigruppi :
I chimici usano la teoria dei gruppi per comprendere la relazione tra la simmetria e le proprietà fisiche di una molecola. Mentre l'ambito della teoria dei gruppi è troppo ampio per essere rigorosamente coperto in questo video, forniremo gli strumenti necessari per applicare la teoria dei gruppi a semplici complessi di coordinazione e mostrare come può essere utilizzata per prevedere il numero di modalità vibrazionali attive IR. Per dimostrare, cammineremo attraverso l'applicazione della teoria dei gruppi alla molecola cis-Mo(CO)4[P(OPh)3]2.
In primo luogo, dobbiamo determinare il gruppo di punti della molecola. I gruppi di punti sono usati per descrivere gli elementi di simmetria presenti in una data molecola. Per determinare il gruppo puntiare di cis-Mo(CO)4[P(OPh)3]2, possiamo usare un diagramma di flusso chiamato albero di simmetria, che pone una serie di domande sugli elementi di simmetria presenti nella molecola ( Figura2). La Tabella 1 riassume tutti gli elementi di simmetria inclusi nell'albero di simmetria. Usando l'albero di simmetria, e assumendo che i ligandi P(OPh)3 siano ligandi punti (ignorando la simmetria di quei ligandi), troviamo che cis-Mo(CO)4[P(OPh)3]2 è nel gruppo di punti C2v.

Figura 2. Albero di simmetria utilizzato per la determinazione del gruppo di punti.
Tabella 1. Elementi di simmetria utilizzati nella determinazione del gruppo di punti.
| Elemento di simmetria | Simbolo utilizzato | Esempio* |
| Identità | E |  |
| Asse di rotazione (rotazione di 360°/n) |
Cn |  |
| Piano speculare orizzontale (riflessione sul piano xy) |
σh | 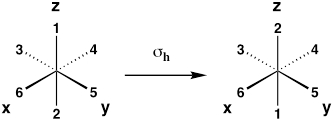 |
| Piano dello specchio verticale (riflessione sul piano xz o yz) |
σv | 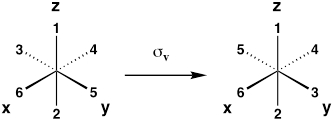 |
| Piano diagonale dello specchio (riflessione tra i piani xz e yz) |
σd | 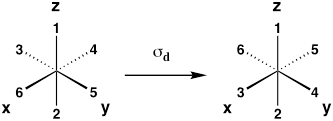 |
| Centro inversione | io | 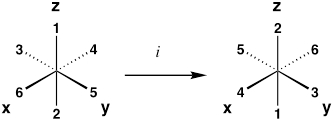 |
| Asse di rotazione improprio (rotazione di 360°/n seguita da riflessione perpendicolare all'asse di rotazione) |
Sn |  |
| *Esempi sono per un complesso ottaedrico, dove i ligandi 1–6 sono equivalenti. Dopo aver eseguito l'operazione, la molecola risultante dovrebbe essere indistinguibile dalla sua configurazione originale. | ||
Per il passaggio successivo, dobbiamo introdurre tabelle di caratteri, che descrivono tutta la simmetria presente all'interno di un determinato gruppo di punti. La tabella dei caratteri per il gruppo di punti C2v è mostrata di seguito.
| C2v | E | C2 | σv(xz) | σv'(yz) | ||
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | −1 | −1 | Rz | xy |
| B1 | 1 | −1 | 1 | −1 | x, Ry | xz |
| B2 | 1 | −1 | −1 | 1 | y, Rx | yz |
Il gruppo di punti è indicato nell'angolo in alto a sinistra della tabella dei caratteri. A destra del gruppo di punti sono elencate tutte le operazioni di simmetria inerenti a tale gruppo di punti. Le righe successive elencano tutte le rappresentazioni di simmetria (rappresentazioni irriducibili, rappresentate dai simboli di Mulliken, cioè A1) contenute in quel gruppo di punti, insieme alla simmetria delle funzioni, che possono dirci della simmetria degli orbitali atomici e del movimento lineare lungo gli assi x, y e z.
Utilizzando la tabella dei caratteri per il gruppo di punti C2v,generiamo una rappresentazione riducibile (Γrosso)dei modi di allungamento C-O nella molecola cis-Mo(CO)4[P(OPh)3]2 (Figura 3). La rappresentazione riducibile, o la combinazione lineare di rappresentazioni irriducibili, può essere generata applicando ciascuna delle operazioni di simmetria all'interno della tabella dei caratteri alle vibrazioni all'interno della molecola e registrando il numero di vibrazioni C-O che rimangono invariate (nella stessa posizione nello spazio). Ad esempio, applicando l'elemento di simmetria dell'identità alle vibrazioni C-O in cis-Mo(CO)4 [P(OPh)3]2, tutte e quattro le frecce vibrazionali rimangono nellastessaposizione. Pertanto, il primo valore nella nostra rappresentazione riducibile è 4. Se continuiamo questo esercizio, generiamo la rappresentazione riducibile mostrata di seguito.
| C2v | E | C2 | σv(xz) | σv'(yz) |
| Γrosso | 4 | 0 | 2 | 2 |
Successivamente, usiamo la tabella dei caratteri C2v per trovare la combinazione lineare di rappresentazioni irriducibili che genera Γrosso per le vibrazioni C-O all'interno di cis-Mo(CO)4[P(OPh)3]2. La riduzione della rappresentazione riducibile può essere ottenuta utilizzando la formula di riduzione mostrata nell'equazione 3.
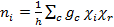 (3)
(3)
dove:
ni = numero di volte in cui la rappresentazione irriducibile i si verifica nella rappresentazione riducibile
h = ordine del gruppo (numero totale di operazioni di simmetria)
c = la classe di funzionamento
gc = numero di operazioni nella classe
χi = carattere della rappresentazione irriducibile per le operazioni della classe
χr = carattere della rappresentazione riducibile per le operazioni della classe
Usando l'equazione 3 per ciascuna delle rappresentazioni irriducibili nella tabella dei caratteri C2v, troviamo che Γrosso = 2A1 + B1 + B2. Tutte e tre le rappresentazioni irriducibili che contribuiscono, A1, B1e B2, sono attive IR perché si trasformano come asse x, y o z (vedere la simmetria delle funzioni nella tabella dei caratteri). Pertanto, prevediamo che cis-Mo(CO)4[P(OPh)3]2 mostrerà 4 modalità di allungamento C-O nel suo spettro IR.
Per riassumere, sono necessari i seguenti passaggi per determinare il numero di modalità vibrazionali attive IR in una molecola:
1. Determinare il gruppo di punti della molecola.
2. Generare una rappresentazione riducibile delle vibrazioni di allungamento C-O all'interno della molecola.
3. Ridurre la rappresentazione riducibile usando l'equazione 3.
4. Identificare il numero di rappresentazioni irriducibili traslazionali presenti nella rappresentazione ridotta dal passaggio 3.
Se seguiamo questi 4 passaggi con trans-Mo(CO)4[P(OPh)3]2, scopriamo che la molecola possiede solo 1 modalità vibrazionale C-O attiva.

Figura 3. CO si estende vibrazionale in cis-Mo(CO)4[P(OPh)3]2.
Procedura
1. Configurazione della linea Schlenk (per una procedura più dettagliata, consultare il video "Schlenk Lines Transfer of Solvent" nella serie Essentials of Organic Chemistry). La sicurezza della linea Schlenk deve essere rivista prima di condurre questo esperimento. La vetreria deve essere ispezionata per le crepe delle stelle prima dell'uso. Prestare attenzione per assicurarsi che O2 non sia condensato nella trappola della linea di Schlenk se si utilizza N2liquido . A temperatura N2 liquida, O2 condensa ed è esplosivo in presenza di solventi organici. Se si sospetta che O2 sia stato condensato o che si osservi un liquido blu nella trappola fredda, lasciare la trappola fredda sotto vuoto dinamico. NON rimuovere latrappola N 2 liquida o spegnere la pompa pervuoto. Nel tempo il liquido O2 sublima nella pompa; è sicuro rimuovere latrappola N 2 liquida solo una volta che tutto l'O2 è sublimare.
- Chiudere la valvola di rilascio della pressione.
- Accendere il gas N2 e la pompa per vuoto.
- Quando il vuoto della linea Schlenk raggiunge la sua pressione minima, preparare la trappola fredda con N2 liquido o ghiaccio secco/acetone.
- Assemblare la trappola fredda.
2. Sintesi di Mo(CO)4[P(OPh)3]2 (Figura 4)1
Nota: Utilizzare tecniche standard della linea Schlenk per la sintesi di Mo(CO)4[P(OPh)3]2 (vedere il video "Sintesi di un metallocene Ti(III) utilizzando la tecnica della linea Schlenk"). I complessi carbonilici metallici sono una fonte di CO libero, che è altamente tossico. L'avvelenamento da monossido di carbonio si verifica quando il CO si lega all'emoglobina, con conseguente significativa riduzione dell'apporto di ossigeno al corpo. Pertanto, è estremamente importante adottare misure di sicurezza appropriate quando si maneggiano e si lavora con complessi metallici carbonilici. Le reazioni che generano CO libero devono essere condotte in una cappa ben ventilata per prevenire l'esposizione al gas tossico.
- Aggiungere 1,6 g (4,92 mmol) di Mo(CO)4(nbd) (nbd = 2,5-Norbornadiene) e 1,6 mL (9,84 mmol) di trifenilfosfito (P(OPh)3) a un matraccio Schlenk da 100 mL e preparare il matraccio Schlenk per il trasferimento cannula del solvente.
Nota: Mo(CO)4(nbd) ((Bicyclo[2.2.1]hepta-2,5-diene)tetracarbonylmolybdenum(0)) può essere acquistato da Sigma Aldrich o sintetizzato utilizzando metodi di letteratura. 2 - Aggiungere 20 ml di diclorometano degassato al matraccio schlenk tramite trasferimento di cannula.
- Mescolare la miscela di reazione per 4 ore a temperatura ambiente sotto N2.
- Rimuovere i volatili sotto vuoto e lavare il precipitato risultante con esani freddi (due lavaggi ciascuno con 10 ml, -78 °C).
- Asciugare il prodotto solido sotto vuoto per 15 min.
- Misurare lo spettro IR del prodotto in una soluzione di esani.
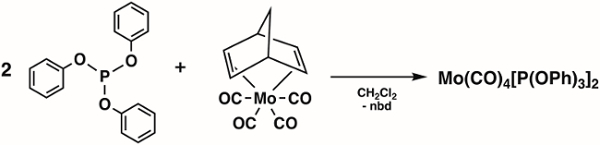
Figura 4. Sintesi di Mo(CO)4[P(OPh)3]2.
Risultati

Figura 5. IR di Mo(CO)4[P(OPh)3]2.
Soluzione IR in idrocarburi saturi (cm-1): 2046 (s), 1958 (s), 1942 (vs).
La quarta risonanza può essere vista solo in condizioni ad alta risoluzione. Pertanto, è possibile, come in questo caso, che si osservino solo 3 delle 4 risonanze.
Sulla base dell'IR ottenuto, possiamo concludere che l'isomero cis di Mo(CO)4[P(OPh)3]2 è stato isolato.
Applicazione e Riepilogo
In questo video, abbiamo imparato come usare la teoria dei gruppi per prevedere il numero di modalità vibrazionali attive IR in una molecola. Abbiamo sintetizzato la molecola Mo(CO)4[P(OPh)3]2 e abbiamo usato IR per determinare quale isomero è stato isolato. Abbiamo osservato che il prodotto aveva tre vibrazioni C-O nel suo spettro IR, che è coerente con l'isomero cis.
La teoria dei gruppi è un potente strumento che viene utilizzato dai chimici non solo per prevedere i modi vibrazionali attivi IR, ma anche vibrazionali, rotazionali e altri modi a bassa frequenza osservati nella spettroscopia Raman. Inoltre, la teoria dei gruppi è implementata nella teoria degli orbitali molecolari (MO), che è il modello più utilizzato per descrivere il legame all'interno di complessi di metalli di transizione. I diagrammi MO, utilizzati dai chimici organici e inorganici, possono prevedere e spiegare la reattività osservata di una molecola.
I complessi carbonilici metallici di1a,2ae3a fila sono ampiamente utilizzati nella sintesi inorganica come precursori metallici per composti organometallici più complessi. Alcuni dei tipi più comuni di reazioni con complessi carbonilici metallici includono la sostituzione del ligando CO, il redox al centro del metallo e l'attacco nucleofilo all'unità CO. Gli stessi complessi carbonilici metallici sono ampiamente utilizzati nella catalisi. Ad esempio, l'idroformilazione, la produzione industriale di aldeidi dagli alcheni, è catalizzato dal complesso carbonilico metallico HCo(CO)3 (Figura 6).

Figura 6. Idroformilazione da parte del complesso carbonilico metallico HCo(CO)3.
Riferimenti
- Fukumoto, K., Nakazawa, H. Geometrical isomerization of fac/mer-Mo(CO)3(phosphite)3 and cis/trans-Mo(CO)4(phosphite)2 catalyzed by Me3SiOSO2CF3. J Organomet Chem. 693(11), 1968-1974 (2008).
- Darensbourg, M. Y., Magdalena, P., Houliston, S. A., Kidwell, K. P., Spencer, D., Chojnacki, S. S., Reibenspies, J. H. Stereochemical nonrigidity in heterobimetallic complexes containing the bent metallocene-thiolate fragment. Inorg Chem. 31(8), 1487-1493 (1992).
- Darensbourg, M. Y., Darensbourg, D. J. Infrared Determination of Stereochemistry in Metal Complexes. J Chem Ed. 47(1), 33-35 (1970).
Vai a...
Video da questa raccolta:

Now Playing
Applicazione della teoria dei gruppi nella spettroscopia infrarossa
Inorganic Chemistry
45.3K Visualizzazioni

Sintesi di un Ti(III) metallocene utilizzando la tecnica della linea Schlenk
Inorganic Chemistry
31.6K Visualizzazioni

Scatola a guanti (Glove Box) e sensori di impurezze
Inorganic Chemistry
18.6K Visualizzazioni

Purificazione del ferrocene per sublimazione
Inorganic Chemistry
54.6K Visualizzazioni

Il metodo di Evans
Inorganic Chemistry
68.6K Visualizzazioni

Diffrazione a raggi X su cristallo singolo e su polveri
Inorganic Chemistry
104.6K Visualizzazioni

Spettroscopia di risonanza paramagnetica elettronica (EPR)
Inorganic Chemistry
25.5K Visualizzazioni

Spettroscopia Mössbauer
Inorganic Chemistry
22.0K Visualizzazioni

Interazione acido-base di Lewis in Ph3P-BH3
Inorganic Chemistry
38.9K Visualizzazioni

Struttura del ferrocene
Inorganic Chemistry
79.6K Visualizzazioni

Teoria degli orbitali molecolari
Inorganic Chemistry
35.4K Visualizzazioni

Paddlewheel a quadruplo legame metallo-metallo
Inorganic Chemistry
15.3K Visualizzazioni

Celle di Grätzel (Dye-sensitized Solar Cells)
Inorganic Chemistry
15.8K Visualizzazioni

Sintesi di un complesso di cobalto (II) legato ad ossigeno
Inorganic Chemistry
51.7K Visualizzazioni

Inizio fotochimico di una reazione di polimerizzazione radicalica
Inorganic Chemistry
16.8K Visualizzazioni