Application of Group Theory to IR Spectroscopy
Genel Bakış
Source: Tamara M. Powers, Department of Chemistry, Texas A&M University
Metal carbonyl complexes are used as metal precursors for the synthesis of organometallic complexes as well as catalysts. Infrared (IR) spectroscopy is one of the most utilized and informative characterization methods of CO containing compounds. Group theory, or the use of mathematics to describe the symmetry of a molecule, provides a method to predict the number of IR active C-O vibrational modes within a molecule. Experimentally observing the number of C-O stretches in the IR is a direct method to establish the geometry and structure of the metal carbonyl complex.
In this video, we will synthesize the molybdenum carbonyl complex Mo(CO)4[P(OPh)3]2, which can exist in the cis- and trans-forms (Figure 1). We will use group theory and IR spectroscopy to determine which isomer is isolated.
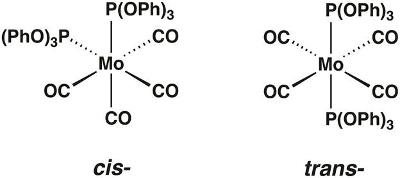
Figure 1. The cis- and trans-isomers of Mo(CO)4[P(OPh)3]2.
İlkeler
Selection Rules:
Selection rules dictate the number of electronic transitions, from one quantum state to another, that are possible for a given molecule. IR spectroscopy probes vibrational transitions from the molecule's ground state, v = 0, to the first excited state, v = 1. The number of degrees of vibrational freedom (normal modes of vibration) for linear and non-linear molecules can be calculated using Equation 1 and Equation 2, respectively.
3N - 5 (1)
3N - 6 (2)
where N = the number of atoms in the molecule
For a normal mode of vibration to be IR active, the molecule's dipole must change. Therefore, any normal modes of vibration where a change in dipole does not occur are IR inactive. The number of active IR modes can be determined using group theory.
Group Theory:
Chemists use group theory to understand the relationship between the symmetry and physical properties of a molecule. While the scope of group theory is too broad to rigorously cover in this video, we will provide the necessary tools needed to apply group theory to simple coordination complexes and show how it can be used to predict the number of IR active vibrational modes. To demonstrate, we will walk through the application of group theory to the molecule cis-Mo(CO)4[P(OPh)3]2.
First, we need to determine the point group of the molecule. Point groups are used to describe the symmetry elements present in a given molecule. To determine the point group of cis-Mo(CO)4[P(OPh)3]2, we can use a flow chart called a symmetry tree, which asks a series of questions about the symmetry elements present in the molecule (Figure 2). Table 1 summarizes all of the symmetry elements included in the symmetry tree. Using the symmetry tree, and assuming that the ligands P(OPh)3 are point ligands (while ignoring the symmetry of those ligands), we find that cis-Mo(CO)4[P(OPh)3]2 is in the point group C2v.

Figure 2. Symmetry tree used for point group determination.
Table 1. Symmetry elements used in point group determination.
| Symmetry element | Symbol used | Example* |
| Identity | E |  |
| Rotation axis (rotation by 360°/n) |
Cn |  |
| Horizontal mirror plane (reflection about xy plane) |
σh | 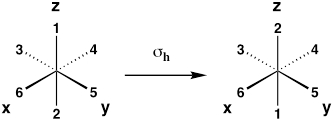 |
| Vertical mirror plane (reflection about xz or yz plane) |
σv | 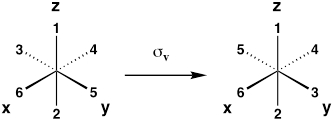 |
| Diagonal mirror plane (reflection between xz and yz planes) |
σd | 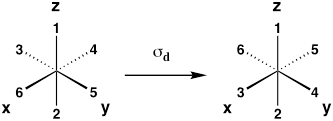 |
| Inversion Center | i | 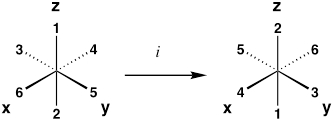 |
| Improper rotation axis (rotation by 360°/n followed by reflection perpendicular to rotation axis) |
Sn |  |
| *Examples are for an octahedral complex, where ligands 1–6 are equivalent. Upon performing the operation, the resulting molecule should be indistinguishable from its original configuration. | ||
For the next step, we need to introduce character tables, which describe all of the symmetry present within a given point group. The character table for the point group C2v is shown below.
| C2v | E | C2 | σv(xz) | σv’(yz) | ||
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | −1 | −1 | Rz | xy |
| B1 | 1 | −1 | 1 | −1 | x, Ry | xz |
| B2 | 1 | −1 | −1 | 1 | y, Rx | yz |
The point group is indicated in the top left-hand corner of the character table. To the right of the point group, all of the symmetry operations inherent to that point group are listed. The subsequent rows list all of the symmetry representations (irreducible representations, represented by Mulliken symbols, i.e.,A1) contained in that point group, along with the symmetry of functions, which can tell us about the symmetry of atomic orbitals as well as linear movement along the x-, y-, and z-axis.
Using the character table for the point group C2v, we generate a reducible representation (Γred) of the C-O stretching modes in the molecule cis-Mo(CO)4[P(OPh)3]2 (Figure 3). The reducible representation, or the linear combination of irreducible representations, can be generated by applying each of the symmetry operations within the character table to the vibrations within molecule and recording the number of C-O vibrations that remain unchanged (in the same position in space). For example, upon applying the identity symmetry element to the C-O vibrations in cis-Mo(CO)4[P(OPh)3]2, all four of the vibrational arrows remain in the same position. Therefore, the first value in our reducible representation is 4. If we continue this exercise, we generate the reducible representation shown below.
| C2v | E | C2 | σv(xz) | σv’(yz) |
| Γred | 4 | 0 | 2 | 2 |
Next, we use the C2v character table to find the linear combination of irreducible representations that generates Γred for the C-O vibrations within cis-Mo(CO)4[P(OPh)3]2. Reduction of the reducible representation can be achieved using the reduction formula shown in Equation 3.
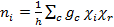 (3)
(3)
where:
ni = number of times the irreducible representation i occurs in the reducible representation
h = order of the group (total number of symmetry operations)
c = the class of operation
gc = number of operations in the class
χi = character of the irreducible representation for the operations of the class
χr = character of the reducible representation for the operations of the class
Using Equation 3 for each of the irreducible representations in the character table C2v, we find that Γred = 2A1 + B1 + B2. All three of the contributing irreducible representations, A1, B1, and B2, are IR active because they transform as either the x-, y-, or z-axis (see the symmetry of functions in the character table). Therefore, we predict that cis-Mo(CO)4[P(OPh)3]2 will exhibit 4 C-O stretching modes in its IR spectrum.
To summarize, the following steps are needed in order to determine the number of IR active vibrational modes in a molecule:
1. Determine the point group of the molecule.
2. Generate a reducible representation of the C-O stretching vibrations within the molecule.
3. Reduce the reducible representation using Equation 3.
4. Identify the number of translational irreducible representations present in the reduced representation from step 3.
If we follow these 4 steps with trans-Mo(CO)4[P(OPh)3]2, we find that the molecule only possesses 1 active C-O vibrational mode.

Figure 3. CO vibrational stretches in cis-Mo(CO)4[P(OPh)3]2.
Prosedür
1. Setup of the Schlenk Line (for a more detailed procedure, please review the "Schlenk Lines Transfer of Solvent" video in the Essentials of Organic Chemistry series). Schlenk line safety should be reviewed prior to conducting this experiment. Glassware should be inspected for star cracks before use. Care should be taken to ensure that O2 is not condensed in the Schlenk line trap if using liquid N2. At liquid N2 temperature, O2 condenses and is explosive in the presence of organic solvents. If it is suspected that O2 has been condensed or a blue liquid is observed in the cold trap, leave the trap cold under dynamic vacuum. Do NOT remove the liquid N2 trap or turn off the vacuum pump. Over time the liquid O2 will sublime into the pump; it is only safe to remove the liquid N2 trap once all of the O2 has sublimed.
- Close the pressure release valve.
- Turn on the N2 gas and the vacuum pump.
- As the Schlenk line vacuum reaches its minimum pressure, prepare the cold trap with either liquid N2 or dry ice/acetone.
- Assemble the cold trap.
2. Synthesis of Mo(CO)4[P(OPh)3]2 (Figure 4)1
Note: Use standard Schlenk line techniques for the synthesis of Mo(CO)4[P(OPh)3]2 (see the "Synthesis of a Ti(III) Metallocene Using Schlenk line Technique" video). Metal carbonyl complexes are a source of free CO, which is highly toxic. Carbon monoxide poisoning occurs when CO binds to hemoglobin, resulting in significant reduction of oxygen supply to the body. Therefore, it is extremely important to take appropriate safety measures when handling and working with metal carbonyl complexes. Reactions that generate free CO need to be conducted in a well-ventilated hood to prevent exposure to the toxic gas.
- Add 1.6 g (4.92 mmol) Mo(CO)4(nbd) (nbd = 2,5-Norbornadiene) and 1.6 mL (9.84 mmol) triphenyl phosphite (P(OPh)3) to a 100 mL Schlenk flask and prepare the Schlenk flask for the cannula transfer of solvent.
Note: Mo(CO)4(nbd) ((Bicyclo[2.2.1]hepta-2,5-diene)tetracarbonylmolybdenum(0)) can be purchased from Sigma Aldrich or synthesized using literature methods.2 - Add 20 mL of degassed dichloromethane to the Schlenk flask via cannula transfer.
- Stir the reaction mixture for 4 h at room temperature under N2.
- Remove the volatiles under vacuum and wash the resulting precipitate with cold hexanes (two washes each with 10 mL, −78 °C).
- Dry the solid product under vacuum for 15 min.
- Measure the IR spectrum of the product in a solution of hexanes.
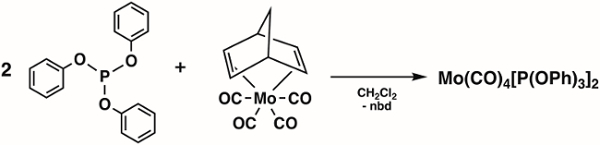
Figure 4. Synthesis of Mo(CO)4[P(OPh)3]2.
Sonuçlar

Figure 5. IR of Mo(CO)4[P(OPh)3]2.
Solution IR in saturated hydrocarbon (cm-1): 2046 (s), 1958 (s), 1942 (vs).
The fourth resonance can only be seen under high-resolution conditions. Therefore, it is possible, as in this case, that only 3 of the 4 resonances are observed.
Based on the obtained IR, we can conclude that cis-isomer of Mo(CO)4[P(OPh)3]2 was isolated.
Başvuru ve Özet
In this video, we learned how to use group theory to predict the number of IR active vibrational modes in a molecule. We synthesized the molecule Mo(CO)4[P(OPh)3]2 and used IR to determine which isomer was isolated. We observed that the product had three C-O vibrations in its IR spectrum, which is consistent with the cis-isomer.
Group theory is a powerful tool that is used by chemists to not only predict IR active vibrational modes, but also vibrational, rotational, and other low-frequency modes observed in Raman spectroscopy. Additionally, group theory is implemented in molecular orbital (MO) theory, which is the most widely used model to describe bonding within transition metal complexes. MO diagrams, used by organic and inorganic chemists, can predict and explain a molecule's observed reactivity.
1st, 2nd, and 3rd row metal carbonyl complexes are used widely in inorganic synthesis as metal precursors for more complex organometallic compounds. Some of the most common types of reactions with metal carbonyl complexes include CO ligand substitution, redox at the metal center, and nucleophilic attack at the CO unit. Metal carbonyl complexes themselves are widely used in catalysis. For example, hydroformylation, the industrial production of aldehydes from alkenes, is catalyzed by the metal carbonyl complex HCo(CO)3 (Figure 6).

Figure 6. Hydroformylation by the metal carbonyl complex HCo(CO)3.
Referanslar
- Fukumoto, K., Nakazawa, H. Geometrical isomerization of fac/mer-Mo(CO)3(phosphite)3 and cis/trans-Mo(CO)4(phosphite)2 catalyzed by Me3SiOSO2CF3. J Organomet Chem. 693(11), 1968-1974 (2008).
- Darensbourg, M. Y., Magdalena, P., Houliston, S. A., Kidwell, K. P., Spencer, D., Chojnacki, S. S., Reibenspies, J. H. Stereochemical nonrigidity in heterobimetallic complexes containing the bent metallocene-thiolate fragment. Inorg Chem. 31(8), 1487-1493 (1992).
- Darensbourg, M. Y., Darensbourg, D. J. Infrared Determination of Stereochemistry in Metal Complexes. J Chem Ed. 47(1), 33-35 (1970).
Atla...
Bu koleksiyondaki videolar:

Now Playing
Application of Group Theory to IR Spectroscopy
Inorganic Chemistry
45.3K Görüntüleme Sayısı

Synthesis Of A Ti(III) Metallocene Using Schlenk Line Technique
Inorganic Chemistry
31.6K Görüntüleme Sayısı

Glovebox and Impurity Sensors
Inorganic Chemistry
18.6K Görüntüleme Sayısı

Purification of Ferrocene by Sublimation
Inorganic Chemistry
54.7K Görüntüleme Sayısı

The Evans Method
Inorganic Chemistry
68.6K Görüntüleme Sayısı

Single Crystal and Powder X-ray Diffraction
Inorganic Chemistry
104.6K Görüntüleme Sayısı

Electron Paramagnetic Resonance (EPR) Spectroscopy
Inorganic Chemistry
25.5K Görüntüleme Sayısı

Mössbauer Spectroscopy
Inorganic Chemistry
22.0K Görüntüleme Sayısı

Lewis Acid-Base Interaction in Ph3P-BH3
Inorganic Chemistry
38.9K Görüntüleme Sayısı

Structure Of Ferrocene
Inorganic Chemistry
79.6K Görüntüleme Sayısı

Molecular Orbital (MO) Theory
Inorganic Chemistry
35.4K Görüntüleme Sayısı

Quadruply Metal-Metal Bonded Paddlewheels
Inorganic Chemistry
15.3K Görüntüleme Sayısı

Dye-sensitized Solar Cells
Inorganic Chemistry
15.8K Görüntüleme Sayısı

Synthesis of an Oxygen-Carrying Cobalt(II) Complex
Inorganic Chemistry
51.7K Görüntüleme Sayısı

Photochemical Initiation Of Radical Polymerization Reactions
Inorganic Chemistry
16.8K Görüntüleme Sayısı
JoVE Hakkında
Telif Hakkı © 2020 MyJove Corporation. Tüm hakları saklıdır