Visualizzazione del flusso oltre un corpo Bluff
Panoramica
Fonte: Ricardo Mejia-Alvarez, Hussam Hikmat Jabbar e Mahmoud N. Abdullatif, Dipartimento di Ingegneria Meccanica, Michigan State University, East Lansing, MI
A causa della natura non lineare delle sue leggi di governo, il movimento fluido induce complicati schemi di flusso. Comprendere la natura di questi modelli è stato oggetto di un intenso esame per secoli. Sebbene i personal computer e i supercomputer siano ampiamente utilizzati per dedurre modelli di flusso dei fluidi, le loro capacità sono ancora insufficienti per determinare l'esatto comportamento del flusso per geometrie complesse o flussi altamente inerziali (ad esempio quando la quantità di moto domina sulla resistenza viscosa). Con questo in mente, sono state sviluppate una moltitudine di tecniche sperimentali per rendere evidenti i modelli di flusso che possono raggiungere regimi di flusso e geometrie inaccessibili agli strumenti teorici e computazionali.
Questa dimostrazione studierà il flusso di fluidi intorno a un corpo bluff. Un corpo bluff è un oggetto che, a causa della sua forma, provoca un flusso separato sulla maggior parte della sua superficie. Questo è in contrasto con un corpo aerodinamico, come un profilo alare, che è allineato nel flusso e causa una minore separazione del flusso. Lo scopo di questo studio è quello di utilizzare le bolle di idrogeno come metodo per visualizzare i modelli di flusso. Le bolle di idrogeno sono prodotte tramite elettrolisi utilizzando una fonte di alimentazione CC immergendo i suoi elettrodi nell'acqua. Le bolle di idrogeno si formano nell'elettrodo negativo, che deve essere un filo molto sottile per garantire che le bolle rimangano piccole e tracciano il movimento del fluido in modo più efficace. Questo metodo è adatto per flussi laminari costanti e instabili e si basa sulle linee di flusso di base che descrivono la natura del flusso intorno agli oggetti. [1-3]
Questo documento si concentra sulla descrizione dell'implementazione della tecnica, compresi i dettagli sull'apparecchiatura e la sua installazione. Quindi, la tecnica viene utilizzata per dimostrare l'uso di due delle linee di flusso di base per caratterizzare il flusso attorno a un cilindro circolare. Queste linee di flusso vengono utilizzate per stimare alcuni importanti parametri di flusso come la velocità del flusso e il numero di Reynolds e per determinare i modelli di flusso.
Principi
In questa configurazione, considereremo un flusso d'acqua costante uniforme con velocità  (soprannominata velocità a flusso libero) che si avvicina a un cilindro circolare (Figura 1). A seconda delle condizioni di flusso caratterizzate dal numero di Reynolds, questo flusso potrebbe diventare instabile e dare origine a uno spargimento di vortici. Lo spargimento di vortici è tipico nel flusso oltre i corpi bluff che, a differenza dei corpi aerodinamici, mostrano la separazione dello strato limite su una porzione sostanziale della loro superficie. Questa separazione dello strato limite porta alla formazione di vortici dietro il corpo che potrebbero eventualmente staccarsi periodicamente nella scia. Quando avviene il distacco periodico, i vortici generano aree alternate di bassa pressione dietro il corpo che potrebbero diventare carichi risonanti se la frequenza di spargimento coincide con la frequenza naturale del corpo. Questo processo di spargimento del vortice è chiamato "strada del vortice di Von Kármàn" (Figura 2). Questo schema ripetuto di vortici vorticosi è causato da una separazione del flusso instabile attorno al corpo del bluff e si verifica in determinati intervalli di numero di Reynolds. Evitare questo scenario è di notevole importanza nella progettazione di strutture ingegneristiche come ciminiere e pilastri del ponte poiché potrebbe causare guasti catastrofici.
(soprannominata velocità a flusso libero) che si avvicina a un cilindro circolare (Figura 1). A seconda delle condizioni di flusso caratterizzate dal numero di Reynolds, questo flusso potrebbe diventare instabile e dare origine a uno spargimento di vortici. Lo spargimento di vortici è tipico nel flusso oltre i corpi bluff che, a differenza dei corpi aerodinamici, mostrano la separazione dello strato limite su una porzione sostanziale della loro superficie. Questa separazione dello strato limite porta alla formazione di vortici dietro il corpo che potrebbero eventualmente staccarsi periodicamente nella scia. Quando avviene il distacco periodico, i vortici generano aree alternate di bassa pressione dietro il corpo che potrebbero diventare carichi risonanti se la frequenza di spargimento coincide con la frequenza naturale del corpo. Questo processo di spargimento del vortice è chiamato "strada del vortice di Von Kármàn" (Figura 2). Questo schema ripetuto di vortici vorticosi è causato da una separazione del flusso instabile attorno al corpo del bluff e si verifica in determinati intervalli di numero di Reynolds. Evitare questo scenario è di notevole importanza nella progettazione di strutture ingegneristiche come ciminiere e pilastri del ponte poiché potrebbe causare guasti catastrofici.

Figura 1. Scorrere oltre un cilindro circolare. Schema della configurazione di base. Un flusso omogeneo con velocità  si avvicina a un cilindro dritto di diametro il cui asse di
si avvicina a un cilindro dritto di diametro il cui asse di  simmetria è perpendicolare alla velocità in avvicinamento.
simmetria è perpendicolare alla velocità in avvicinamento.
Il numero di Reynolds è un parametro adimensionale definito come il rapporto tra forze inerziali e forze viscose:
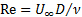 (1)
(1)
Dove 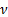 è la viscosità cinematica del fluido,
è la viscosità cinematica del fluido,  una velocità caratteristica
una velocità caratteristica  (nel caso di specie) e
(nel caso di specie) e 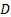 il diametro del cilindro. Il numero di Reynolds è probabilmente il parametro più importante nella caratterizzazione del flusso di fluido e sarà utilizzato in tutto il presente esperimento come metrica per l'emergere della via del vortice di Von Kármàn. In particolare, quando il numero di Reynolds è intorno a 5, il flusso mostra due vortici controrotanti stabili dietro il cilindro. All'aumentare del numero di Reynolds, questi due vortici si allungano nella direzione del flusso. Quando il numero di Reynolds raggiunge un valore di circa 37, la scia diventa instabile e inizia a oscillare sinusoidale a causa di uno squilibrio tra pressione e quantità di moto. Un ulteriore aumento del numero di Reynolds fino a 47 fa sì che i due vortici controrotanti si stacchino dal cilindro in una sequenza alternata che segue l'oscillazione sinusoidale della scia [4,5,6].
il diametro del cilindro. Il numero di Reynolds è probabilmente il parametro più importante nella caratterizzazione del flusso di fluido e sarà utilizzato in tutto il presente esperimento come metrica per l'emergere della via del vortice di Von Kármàn. In particolare, quando il numero di Reynolds è intorno a 5, il flusso mostra due vortici controrotanti stabili dietro il cilindro. All'aumentare del numero di Reynolds, questi due vortici si allungano nella direzione del flusso. Quando il numero di Reynolds raggiunge un valore di circa 37, la scia diventa instabile e inizia a oscillare sinusoidale a causa di uno squilibrio tra pressione e quantità di moto. Un ulteriore aumento del numero di Reynolds fino a 47 fa sì che i due vortici controrotanti si stacchino dal cilindro in una sequenza alternata che segue l'oscillazione sinusoidale della scia [4,5,6].
La frequenza con cui i vortici vengono espulsi dal cilindro non è costante; varia con il valore del numero di Reynolds. La frequenza di spargimento è caratterizzata dal numero di Strouhal, che è l'altro parametro adimensionale di rilevanza in questa particolare configurazione del flusso del fluido:
 (2)
(2)
Ecco, ![]() è la frequenza di spargimento del vortice e le scale di lunghezza e velocità sono le stesse del numero di Reynolds. La frequenza di spargimento del vortice può quindi essere caratterizzata dal numero di Strouhal come funzione lineare della radice quadrata inversa del numero di Reynolds [7]:
è la frequenza di spargimento del vortice e le scale di lunghezza e velocità sono le stesse del numero di Reynolds. La frequenza di spargimento del vortice può quindi essere caratterizzata dal numero di Strouhal come funzione lineare della radice quadrata inversa del numero di Reynolds [7]:
 (3)
(3)
Questa funzione non è sempre monotona, mostra ulteriori transizioni a seguito di instabilità secondarie dovute alla non linearità del flusso del fluido. Di conseguenza, i coefficienti  e
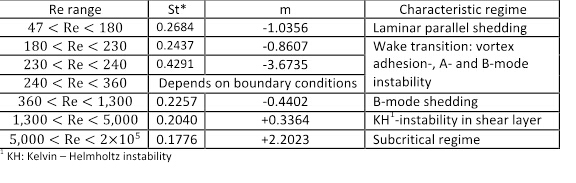
e 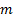 cambierebbero in base all'intervallo di numeri di Reynolds. La tabella 1 mostra i valori di questi coefficienti per i regimi di flusso che sono stati ben caratterizzati in letteratura [7].
cambierebbero in base all'intervallo di numeri di Reynolds. La tabella 1 mostra i valori di questi coefficienti per i regimi di flusso che sono stati ben caratterizzati in letteratura [7].
Durante i presenti esperimenti, utilizzeremo linee di flusso per studiare il flusso esterno attorno a un cilindro circolare. Queste linee di flusso sono definite come segue:
• Pathline: percorso che una particella fluida segue mentre si muove con il flusso.
• Streakline: locus continuo di tutte le particelle fluide il cui moto ha avuto origine nella stessa posizione spaziale.
• Timeline: insieme di particelle fluide che sono state taggate nello stesso istante di tempo mentre formavano un locus continuo.
• Streamline: linea continua che è ovunque tangente al campo di velocità in un istante nel tempo.
Le prime tre linee sono relativamente facili da generare sperimentalmente, mentre le linee aerodinamiche sono semplicemente un concetto matematico che in generale deve essere prodotto post-elaborando una cattura istantanea del campo di velocità. Mentre questo è sempre vero, l'analisi semplifica in modo significativo i flussi costanti perché le linee di percorso, le linee striate e le linee di flusso coincidono tra loro. Al contrario, queste linee generalmente non coincidono tra loro in flussi instabili. L'implementazione di questa tecnica è generalmente semplice e richiede solo attrezzature a basso costo, al contrario di tecniche più sofisticate e costose come la Particle Image Velocimetry [1], la Particle Tracking Velocimetry [8,9] e la Molecular Tagging Velocimetry [10].

Figura 2. Risultati rappresentativi. (A) foglio continuo di bolle di idrogeno che mostra linee striature a seguito di perturbazioni a monte. L'ombra proiettata dall'asta viene utilizzata per determinare la conversione da macchina a unità reali. Viene anche illustrato un ciclo di spargimento del vortice per aiutare a determinare la frequenza di spargimento in modo appropriato. (B) tempistiche generate con bolle di idrogeno. Poiché la frequenza temporale è ben definita, possono essere utilizzate per misurare con precisione la velocità del flusso; per questa stima verranno utilizzate le linee temporali racchiuse nelle linee rosse. Fare clic qui per visualizzare una versione più grande di questa figura.
Tabella 1. Valori dei coefficienti  e
e  per diversi intervalli numerici di Reynolds (da [8]).
per diversi intervalli numerici di Reynolds (da [8]).
Procedura
1. Per produrre un foglio continuo di bolle:
- Impostare l'apparecchiatura in base allo schema elettrico mostrato nella Figura 3.
- Fissare l'elettrodo positivo nell'acqua all'estremità a valle della sezione di prova (vedere la Figura 4 per riferimento).
- Fissare l'elettrodo negativo a monte e vicino al punto di interesse per rilasciare le bolle nel flusso prima che il flusso raggiunga l'oggetto di studio (vedere la Figura 4 per riferimento). L'acqua completa il circuito tra i due elettrodi.
- Accendere l'impianto di flusso
- Impostare la manopola del regolatore di frequenza in posizione 2. Questo stabilirà una portata di circa 9x10-4 m3/s.
- Accendere l'alimentatore DC e aumentare la tensione fino a circa 25 V, la corrente si posizionerà intorno ai 190 mA.
- Impostare la forma d'onda nel generatore di segnali su Onda quadra (simbolo:
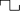 ). Questo genera un segnale quadrato 0 V - 5 V che attiva il relè a stato solido (chiudendo il circuito) nella sua posizione alta e lo apre in posizione bassa
). Questo genera un segnale quadrato 0 V - 5 V che attiva il relè a stato solido (chiudendo il circuito) nella sua posizione alta e lo apre in posizione bassa - Per questo caso particolare, la frequenza dell'onda quadra non è importante. Deve solo essere diverso da zero.
- Massimizzare l'offset CC (+5 V) nel generatore di segnale. Con questa impostazione, il circuito è sempre chiuso e il sistema genera bolle in modo continuo.
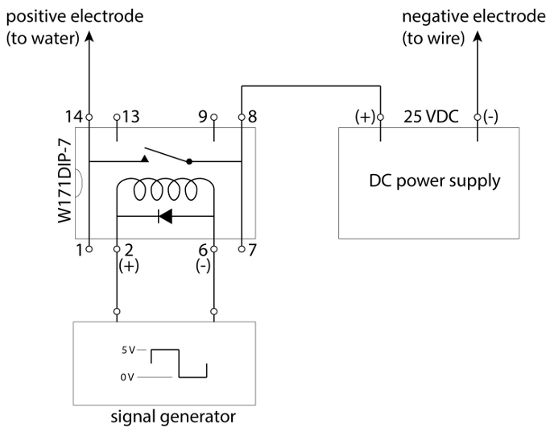
Figura 3. Diagramma delle connessioni.

Figura 4. Sezione di prova. Il flusso va da sinistra a destra. L'elettrodo negativo genera uno strato di bolle di idrogeno che vengono spazzate via con il flusso. L'elettrodo positivo è posto all'estremità a valle della sezione di prova per evitare i suoi disturbi. Fare clic qui per visualizzare una versione più grande di questa figura.
2. Per produrre scadenze:
- Accendere l'impianto di flusso
- Impostare la manopola del regolatore di frequenza in posizione 2. Questo stabilirà una portata di circa 9x10-4 m3/s.
- Accendere l'alimentatore DC e aumentare la tensione fino a circa 25 V, la corrente si posizionerà intorno ai 190 mA.
- Impostare la forma d'onda nel generatore di segnali su Onda quadra (simbolo:
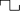 ). Questo genera un segnale quadrato 0 V - 5 V che attiva il relè a stato solido (chiudendo il circuito) nella sua posizione alta e lo disattiva (aprendo il circuito) in posizione bassa
). Questo genera un segnale quadrato 0 V - 5 V che attiva il relè a stato solido (chiudendo il circuito) nella sua posizione alta e lo disattiva (aprendo il circuito) in posizione bassa - Impostare l'offset CC nel generatore di segnali a +1 V.
- Impostare la frequenza dell'onda quadra nel generatore di segnale a 10 Hz.
- Impostare la simmetria dell'onda quadra leggermente negativa (-2) per aumentare lo spazio tra le linee temporali conservando la giusta frequenza.
3. Utilizzare le linee di flusso per studiare le strade del vortice di Von Kármàn:
- Misurare il diametro dell'asta,
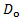 , utilizzando una pinza. Utilizzare unità S.I. per questa misurazione (m).
, utilizzando una pinza. Utilizzare unità S.I. per questa misurazione (m). - Fissare un'asta cilindrica a valle dell'elettrodo negativo.
- Proiettare la luce della lampada a scarica ad alta intensità sullo strato di bolle di idrogeno. Assicurarsi che la luce non sia direttamente dietro la linea di visualizzazione per evitare la sovrasaturazione del sistema di imaging
- Allineare il sistema di visualizzazione con l'asta; in modo che solo la punta circolare sia visibile davanti alla telecamera.
- Aggiungere un segno nella finestra di visualizzazione e a valle dell'asta per utilizzarlo come riferimento per contare i cicli di vortice per unità di tempo.
4. Analisi dei dati per il flusso oltre un cilindro circolare:
- Determinazione del fattore di conversione da unità macchina a unità spaziali reali:
- Misurare la larghezza dell'ombra proiettata dall'asta sul foglio a bolle (vedere la figura 2(A) per riferimento). Prendi questa misurazione direttamente sull'asta per evitare distorsioni con la distanza. Questo è il diametro dell'asta nelle unità della macchina
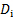 ,(punti o pixel, a seconda del formato)
,(punti o pixel, a seconda del formato) - Utilizzare la seguente equazione per determinare il fattore di conversione dalle unità macchina alle unità del mondo reale:

- Misurare la larghezza dell'ombra proiettata dall'asta sul foglio a bolle (vedere la figura 2(A) per riferimento). Prendi questa misurazione direttamente sull'asta per evitare distorsioni con la distanza. Questo è il diametro dell'asta nelle unità della macchina
- Determinazione della velocità del flusso:
- Scegli un gruppo di linee temporali non distorte a monte del corpo del bluff.
- Misurare la distanza tra la prima e l'ultima linea temporale in unità
 macchina (punti o pixel).
macchina (punti o pixel). - Contare il numero di sequenze temporali nel gruppo,
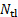 .
. - Prendi nota della frequenza del segnale dell'onda quadra prodotta dal generatore di segnale,
 .
. - Determinare la velocità del flusso in avvicinamento dalla seguente equazione:

- Determinazione del numero di Reynolds:
- Trovare la viscosità cinematica del fluido di lavoro (ad es. acqua
 m2/s).
m2/s). - Calcola il numero di Reynolds usando l'equazione (1). Per questo, considerando il diametro dell'asta (
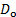 ) misurato nel passo 3.1, la velocità di avvicinamento ( )
) misurato nel passo 3.1, la velocità di avvicinamento ( )  determinata con l'equazione (5) e la viscosità cinematica determinata nel passaggio 4.3.1
determinata con l'equazione (5) e la viscosità cinematica determinata nel passaggio 4.3.1
- Trovare la viscosità cinematica del fluido di lavoro (ad es. acqua
- Determinazione del numero di Strouhal: i vortici sulla scia dell'asta si muovono a una velocità diversa rispetto alle linee temporali nel flusso libero. Quindi, la frequenza di spargimento del vortice deve essere stimata in modo indipendente.
- Definite un riferimento fisso a valle dell'asta. Questo riferimento potrebbe essere una stringa fine attaccata all'esterno del tunnel o una linea digitale aggiunta a un video del processo di flusso.
- Contare il numero di cicli di spargimento di
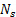 vortici, , attraversando il riferimento durante un periodo di tempo definito
vortici, , attraversando il riferimento durante un periodo di tempo definito  . Un ciclo di spargimento di vortici è illustrato nella Figura 2(A).
. Un ciclo di spargimento di vortici è illustrato nella Figura 2(A). - Calcola la frequenza di spargimento dalla seguente equazione:
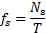
- Usa i risultati delle equazioni (5) e (6) nell'equazione (2) per calcolare il numero di Strouhal.
Risultati
La Figura 2 mostra due risultati rappresentativi della visualizzazione della bolla di idrogeno di una strada del vortice di Von Kármàn. La Figura 2(A) mostra un esempio di un campo di linee striata, come evidenziato da disturbi nel foglio di bolle di idrogeno. Questa immagine viene utilizzata per estrarre il diametro dell'asta nelle unità della macchina. La Figura 2(B) mostra un esempio di un campo di sequenze temporali. Questa immagine viene utilizzata per stimare la velocità del fluido in avvicinamento. I parametri estratti da questo particolare esperimento sono riassunti nella tabella 2.
Tabella 2. Risultati rappresentativi per il flusso oltre un cilindro circolare.
| Parametro | Valore |
| D_o | 0,003 m |
| D_i | 14.528 punti |
| f_s | 2,169 Hz |
| f_tl | 10 Hz |
| L | 130.167 "pts" |
| M | 4842,67 "pts" ∕"m" |
| N_s | 60 |
| N_tl | 7 |
| T | 27,66 s |
| U_∞ | 0,0384 m/s |
| ν | 1,004×[10]^(-6) m2/s |
| Ri | 115 |
| San | 0.169 |
Poiché il numero di Reynolds è 115 per il presente esempio, la validità di questo risultato può essere testata usando l'equazione (3) per 
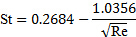 (7)
(7)
Da cui otteniamo:
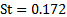 (8)
(8)
Dopo aver confrontato questa stima con il nostro risultato sperimentale (vedi tabella 2 per riferimento), possiamo concludere che il nostro esperimento ha offerto un risultato soddisfacente. La Figura 5 mostra una serie di risultati sperimentali confrontati con le previsioni dell'equazione (7).

Figura 5. Risultati sperimentali. Confronto degli attuali risultati sperimentali con le previsioni della relazione tra il numero di Reynolds e il numero di Strouhal per il flusso oltre un cilindro circolare.
Applicazione e Riepilogo
In questo studio, l'uso di bolle di idrogeno è stato dimostrato per estrarre informazioni qualitative e quantitative dalle immagini del flusso attorno a un cilindro circolare. Le informazioni quantitative estratte da questi esperimenti includevano la velocità del flusso libero ( ), la  frequenza di spargimento di vortici (
frequenza di spargimento di vortici ( 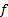 ), il numero di Reynolds (Re) e il numero di Strouhal (St). In particolare, i risultati per St vs Re hanno mostrato un ottimo accordo con studi precedenti [3].
), il numero di Reynolds (Re) e il numero di Strouhal (St). In particolare, i risultati per St vs Re hanno mostrato un ottimo accordo con studi precedenti [3].
A causa della lentezza utilizzata negli esperimenti in corso, le perturbazioni nel foglio di bolle producono uno strato di bolle striate. Queste strisce sono fondamentalmente strisce. Mentre il foglio di bolle di idrogeno viaggia a valle, queste linee striature si ispessiscono e diventano più irregolari. Questo è il risultato dell'intensità della turbolenza nel flusso libero. L'effetto si attenua man mano che la velocità del tunnel aumenta poiché le bolle escono dalla sezione di prova prima di presentare una dispersione significativa. Le linee di striature possono anche essere prodotte in luoghi preselezionati rivestendo il filo lasciando piccole parti di esso esposte all'acqua.
Il comportamento del flusso corrente è direttamente applicabile al flusso oltre le strutture ingegneristiche come i pilastri di ponti e piattaforme petrolifere offshore, le torri delle turbine eoliche o i pali delle linee elettriche per citarne alcuni. E in effetti, questo comportamento è esibito da corpi bluff con geometrie diverse da quelle cilindriche come i grattacieli. Dato che i vortici generano interazioni fluido-struttura che fanno oscillare le strutture, conoscere le frequenze di spargimento del vortice a cui una determinata struttura sarà esposta è fondamentale per la sua progettazione. A questo proposito, l'ingegnere deve assicurarsi che la frequenza naturale della struttura non sia tale da risuonare con la frequenza di spargimento del vortice, perché questo effetto porterà inevitabilmente a un catastrofico fallimento della struttura. Utilizzando le leggi di ridimensionamento appropriate [10] e le bolle di idrogeno in un tunnel d'acqua, un ingegnere può simulare l'interazione del flusso con una struttura prima della sua costruzione per assicurarsi che il suo design sia sicuro o per scoprire se ha bisogno di modifiche.
Oltre ai corpi bluff, la visualizzazione delle bolle di idrogeno è uno strumento molto potente per studiare il flusso intorno a corpi aerodinamici come profili alari o scafi di navi. Facendo uso di linee di flusso generate con questa tecnica, è possibile determinare parametri come l'angolo di attacco a cui avviene lo stallo, o anche stimare le caratteristiche di sollevamento in base alla velocità del flusso. Ancora più importante, il modello di distorsione delle linee fluide aiuterà l'ingegnere a ottimizzare il suo design.
La visualizzazione con bolle di idrogeno non è limitata ai flussi esterni come sopra menzionato. Questo metodo può anche essere utilizzato per osservare il flusso attraverso canali aperti o sistemi di flusso completamente confinati. In quest'ultimo caso, le pareti dovranno essere trasparenti per garantire l'accesso ottico. Ad esempio, se si è interessati a progettare un diffusore di flusso per il flusso subsonino, le bolle di idrogeno possono essere utilizzate per determinare le condizioni geometriche e di flusso per le quali il diffusore mostrerà separazione e instabilità del flusso. Sulla base di queste osservazioni, il progetto potrebbe essere ottimizzato sperimentalmente per garantirne la corretta funzionalità.
Riferimenti
- Zöllner, F. Leonardo da Vinci 1452-1519: sketches and drawings, Taschen, 2004.
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Adrian, Ronald J., and Jerry Westerweel. Particle Image Velocimetry. Cambridge University Press, 2011.
- Gerrard, J. H., The wakes of cylindrical bluff bodies at low Reynolds number, Phil. Trans. Roy. Soc. (London) Ser. A, Vol. 288, No. 1354, pp. 351-382 (1978)
- Coutanceau, M. and Bouard, R., Experimental determination of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow, J. Fluid Mech., Vol. 79, Part 2, pp. 231-256 (1977)
- Kovásznay, L. S. G., Hot-wire investigation of the wake behind cylinders at low Reynolds numbers, Proc. Roy. Soc. (London) Ser. A, Vol. 198, pp. 174-190 (1949)
- Fey, U., M. König, and H. Eckelmann. A new Strouhal-Reynolds-number relationship for the circular cylinder in the range
 . Physics of Fluids, 10(7):1547, 1998.
. Physics of Fluids, 10(7):1547, 1998. - Maas, H.-G., A. Grün, and D. Papantoniou. Particle Tracking in three dimensional turbulent flows - Part I: Photogrammetric determination of particle coordinates. Experiments in Fluids Vol. 15, pp. 133-146, 1993.
- Malik, N., T. Dracos, and D. Papantoniou Particle Tracking in three dimensional turbulent flows - Part II: Particle tracking. Experiments in Fluids Vol. 15, pp. 279-294, 1993.
- Tropea, C., A.L. Yarin, and J.F. Foss. Springer Handbook of Experimental Fluid Mechanics. Vol. 1. Springer Science & Business Media, 2007.
- Monaghan, J. J., and J. B. Kajtar. Leonardo da Vinci's turbulent tank in two dimensions. European Journal of Mechanics-B/Fluids. 44:1-9, 2014.
- Becker, H.A. Dimensionless parameters: theory and methodology. Wiley, 1976.
Vai a...
Video da questa raccolta:

Now Playing
Visualizzazione del flusso oltre un corpo Bluff
Mechanical Engineering
11.9K Visualizzazioni

Galleggiabilità e trascinamento su corpi immersi
Mechanical Engineering
30.0K Visualizzazioni

Stabilità dei vasi galleggianti
Mechanical Engineering
22.6K Visualizzazioni

Propulsione e spinta
Mechanical Engineering
21.7K Visualizzazioni

Reti di tubazioni e perdite di carico
Mechanical Engineering
58.1K Visualizzazioni

Raffreddamento ed ebollizione
Mechanical Engineering
7.7K Visualizzazioni

Salti idraulici
Mechanical Engineering
41.0K Visualizzazioni

Analisi dello scambiatore di calore
Mechanical Engineering
28.0K Visualizzazioni

Introduzione alla refrigerazione
Mechanical Engineering
24.7K Visualizzazioni

Anemometria a filo caldo
Mechanical Engineering
15.6K Visualizzazioni

Misurazione di flussi turbolenti
Mechanical Engineering
13.5K Visualizzazioni

Getto che incide su una piastra inclinata
Mechanical Engineering
10.7K Visualizzazioni

Conservazione dell'energia come approccio all'analisi del sistema
Mechanical Engineering
7.4K Visualizzazioni

Conservazione di massa e misure di portata
Mechanical Engineering
22.6K Visualizzazioni

Determinazione delle forze di impingement su una piastra piana con il metodo del volume di controllo
Mechanical Engineering
26.0K Visualizzazioni