Visualización de flujo más allá de un cuerpo no fuselado
Visión general
Fuente: Ricardo Mejía-Alvarez, Hussam Hikmat Jabbar y Mahmoud Abdullatif N., Departamento de ingeniería mecánica, Universidad Estatal de Michigan, East Lansing, MI
Debido a la naturaleza no lineal de sus leyes gobierno, movimiento fluido induce patrones de flujo complicados. Entender la naturaleza de estos patrones ha sido objeto de intenso escrutinio por siglos. Aunque las computadoras personales y supercomputadoras se utilizan extensivamente para deducir patrones de flujo de fluidos, sus capacidades son todavía insuficientes para determinar el comportamiento del flujo exacto para geometrías complejas o flujos altamente inerciales (por ejemplo cuando impulso domina resistencia viscosa). Con esto en mente, una multitud de técnicas experimentales para hacer flujo han desarrollado patrones evidentes que puede llegar a flujo regímenes y geometrías de herramientas inaccesibles a teórica y computacional.
Esta demostración investigará fluido alrededor de un cuerpo del pen # asco. Un cuerpo del pen # asco es un objeto que, debido a su forma, causas separaron flujo sobre la mayor parte de su superficie. Esto está en contraste con un cuerpo aerodinámico, como una superficie de sustentación, que se alinea en la corriente y produce menor separación del flujo. El propósito de este estudio es utilizar burbujas de hidrógeno como un método para visualizar patrones de flujo. Se producen las burbujas de hidrógeno vía electrólisis usando una fuente de alimentación DC sumergiendo sus electrodos en el agua. Se forman burbujas de hidrógeno en el electrodo negativo, que debe ser un alambre muy fino para que las burbujas siguen siendo pequeñas y seguimiento más eficaz un movimiento fluido. Este método es adecuado para flujos laminares estables e inestables y se basa en las líneas de flujo básicos que describen la naturaleza del flujo alrededor de objetos. [1-3]
Este trabajo se centra en describir la aplicación de la técnica, incluyendo los detalles sobre el equipo y su instalación. Entonces, la técnica se utiliza para demostrar el uso de dos de las líneas de flujo de conceptos básicos para caracterizar el flujo alrededor de un cilindro circular. Estas líneas de flujo se utilizan para estimar algunos parámetros importantes del flujo como la velocidad de flujo y el número de Reynolds y para determinar los patrones de flujo.
Principios
En esta configuración, tendremos en cuenta un caudal de agua con velocidad constante uniforme  (conocido como velocidad de flujo libre) a un cilindro circular (Figura 1). Dependiendo de las condiciones de flujo caracterizado por el número de Reynolds, este flujo puede desestabilizarse y dar lugar a derramamiento en vórtice. Vertimiento del vórtice es típico en flujo más allá de cuerpos faroles que, a diferencia de cuerpo aerodinámico, exhiben separación de capa límite sobre una porción substancial de su superficie. Esta separación de capa límite conduce a la formación de remolinos detrás del cuerpo que eventualmente podría soltar periódicamente en la estela. Cuando ocurre la separación periódica, los vórtices generan alternadas zonas de baja presión detrás del cuerpo que podría convertirse en cargas resonantes si la frecuencia del vertimiento coincide con la frecuencia natural del cuerpo. Este vórtice vertimiento proceso se llama "Kármàn Von vortex street" (Figura 2). Este patrón repetitivo de remolinos remolinos es causado por la separación inestable flujo alrededor del cuerpo del farol y se produce en ciertas gamas del número de Reynolds. Evitar esta situación es de gran importancia en el diseño de estructuras de ingeniería como chimeneas y pilares de puente ya que podría resultar en una falla catastrófica.
(conocido como velocidad de flujo libre) a un cilindro circular (Figura 1). Dependiendo de las condiciones de flujo caracterizado por el número de Reynolds, este flujo puede desestabilizarse y dar lugar a derramamiento en vórtice. Vertimiento del vórtice es típico en flujo más allá de cuerpos faroles que, a diferencia de cuerpo aerodinámico, exhiben separación de capa límite sobre una porción substancial de su superficie. Esta separación de capa límite conduce a la formación de remolinos detrás del cuerpo que eventualmente podría soltar periódicamente en la estela. Cuando ocurre la separación periódica, los vórtices generan alternadas zonas de baja presión detrás del cuerpo que podría convertirse en cargas resonantes si la frecuencia del vertimiento coincide con la frecuencia natural del cuerpo. Este vórtice vertimiento proceso se llama "Kármàn Von vortex street" (Figura 2). Este patrón repetitivo de remolinos remolinos es causado por la separación inestable flujo alrededor del cuerpo del farol y se produce en ciertas gamas del número de Reynolds. Evitar esta situación es de gran importancia en el diseño de estructuras de ingeniería como chimeneas y pilares de puente ya que podría resultar en una falla catastrófica.

Figura 1 . Fluir de un cilindro circular. Esquema de configuración básica. Un flujo homogéneo con velocidad  se acerca a un cilindro recto de diámetro
se acerca a un cilindro recto de diámetro  cuyo eje de simetría es perpendicular a la velocidad que se aproxima.
cuyo eje de simetría es perpendicular a la velocidad que se aproxima.
El número de Reynolds es un parámetro adimensional definido como el cociente de inercia fuerzas a las fuerzas viscosas:
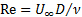 (1)
(1)
Donde 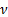 es la viscosidad cinemática del líquido,
es la viscosidad cinemática del líquido,  una velocidad característica (
una velocidad característica ( en el presente caso), y
en el presente caso), y 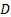 el diámetro del cilindro. El número de Reynolds es el parámetro más importante en la caracterización del flujo flúido y se utilizará en el presente experimento, como la métrica para la aparición de la calle del vórtice de Von Kármàn. En particular, cuando el número de Reynolds es aproximadamente 5, el flujo exhibe dos vórtices en rotación estables detrás el cilindro. A medida que aumenta el número de Reynolds, estos dos vórtices alargados en la dirección del flujo. Cuando el número de Reynolds alcanza un valor de aproximadamente 37, después se vuelve inestable y comienza a oscilar sinusoidal como resultado de un desequilibrio entre la presión y el impulso. Un mayor incremento en el número de Reynolds hasta 47 causa los dos vórtices contra-rotación soltar el cilindro en una secuencia alterna que sigue la oscilación sinusoidal tras [4,5,6].
el diámetro del cilindro. El número de Reynolds es el parámetro más importante en la caracterización del flujo flúido y se utilizará en el presente experimento, como la métrica para la aparición de la calle del vórtice de Von Kármàn. En particular, cuando el número de Reynolds es aproximadamente 5, el flujo exhibe dos vórtices en rotación estables detrás el cilindro. A medida que aumenta el número de Reynolds, estos dos vórtices alargados en la dirección del flujo. Cuando el número de Reynolds alcanza un valor de aproximadamente 37, después se vuelve inestable y comienza a oscilar sinusoidal como resultado de un desequilibrio entre la presión y el impulso. Un mayor incremento en el número de Reynolds hasta 47 causa los dos vórtices contra-rotación soltar el cilindro en una secuencia alterna que sigue la oscilación sinusoidal tras [4,5,6].
La frecuencia con que vórtices son arrojar el cilindro no es constante; varía con el valor del número de Reynolds. Frecuencia del vertimiento se caracteriza por el número de Strouhal, que es el otro parámetro adimensional de relevancia en esta configuración particular fluido:
 (2)
(2)
Aquí, ![]() es la frecuencia del vertimiento de vórtice y las escalas de longitud y velocidad son los mismos que el número de Reynolds. Frecuencia del vertimiento del vórtice puede caracterizarse entonces por el número de Strouhal como una función lineal de la inversa raíz cuadrada del número de Reynolds [7]:
es la frecuencia del vertimiento de vórtice y las escalas de longitud y velocidad son los mismos que el número de Reynolds. Frecuencia del vertimiento del vórtice puede caracterizarse entonces por el número de Strouhal como una función lineal de la inversa raíz cuadrada del número de Reynolds [7]:
 (3)
(3)
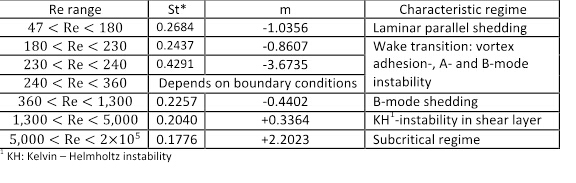
Esta función no es siempre monótona, exhibe más transiciones debido a inestabilidades secundarias debidas a la no linealidad del flujo. Como resultado, los coeficientes de  y
y 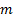 cambiaría según la gama del número de Reynolds. Tabla 1 muestra los valores de estos coeficientes para los regímenes de flujo que han sido bien caracterizados en la literatura [7].
cambiaría según la gama del número de Reynolds. Tabla 1 muestra los valores de estos coeficientes para los regímenes de flujo que han sido bien caracterizados en la literatura [7].
Durante los presentes experimentos, utilizamos líneas de flujo para el estudio de flujo externo alrededor de un cilindro circular. Estas líneas de flujo se definen como sigue:
• Pathline: camino que sigue una partícula de fluido se mueve con el flujo.
• Streakline: locus continua de todas las partículas de líquido cuyo movimiento originado en la misma ubicación espacial.
• Línea de tiempo: conjunto de partículas de fluido que se marcaron en el mismo instante de tiempo formando un locus continuado.
• Optimizada: línea continua que está en todas partes tangente al campo de velocidad en un instante en el tiempo.
Las tres primeras líneas son relativamente fáciles de generar experimentalmente, mientras que los líneas son simplemente un concepto matemático que en general tienen que ser producidos por procesamiento posterior una captura instantánea del campo de velocidad. Esto siempre es cierto, simplifica significativamente el análisis en flujo constante porque Trayetorias, línea y líneas coinciden entre sí. Por el contrario, estas líneas no generalmente coinciden entre sí en flujos inestables. La aplicación de esta técnica es generalmente simple y requiere solamente equipos de bajo coste, en comparación con técnicas más sofisticadas y costosas como Particle Image Velocimetry [1], Particle Tracking Velocimetry [8,9] y marcado Molecular Velocimetry [10].

Figura 2 . Resultados representativos. (A) hoja continua de burbujas de hidrógeno que muestra la línea como resultado de perturbaciones aguas arriba. La sombra de la varilla se utiliza para determinar la conversión de la máquina en unidades reales. También se ilustra un vórtice vertimiento ciclo para ayudar a determinar la frecuencia del vertimiento apropiadamente. (B) plazos generada con burbujas de hidrógeno. Puesto que la frecuencia de línea de tiempo está bien definido, pueden ser utilizados para medir la velocidad de flujo con precisión; contando los plazos dentro de las líneas rojas se utilizará para la estimación de esta. Haga clic aquí para ver una versión más grande de esta figura.
Tabla 1 . Valores de los coeficientes  y
y  para Reynolds diferentes número de intervalos (de [8]).
para Reynolds diferentes número de intervalos (de [8]).
Procedimiento
1. para producir una hoja continua de burbujas:
- Configurar el equipo según el esquema eléctrico que se muestra en la figura 3.
- Fijar el electrodo positivo en el agua en el extremo aguas abajo de la sección de prueba (ver figura 4 para la referencia).
- Fijar el electrodo negativo aguas arriba y cerca del punto de interés para liberar las burbujas en la corriente antes de que el flujo llegue al objeto de estudio (ver figura 4 para la referencia). El agua completa el circuito entre los dos electrodos.
- Gire en la facilidad de flujo
- Ajuste el disco del controlador de frecuencia a posición 2. Esto establecerá un caudal de aproximadamente 9 x 10-4 m3/s.
- Encienda la fuente de alimentación y aumentar el voltaje hasta unos 25 V, la corriente se fijó alrededor 190 mA.
- Establecer la forma de onda en el generador de señal a onda cuadrada (símbolo:
 ). Esto genera un 0 V - señal cuadrada de 5 V que activa el relé de estado sólido (cerrando el circuito) en la posición alta y lo abre en la posición baja
). Esto genera un 0 V - señal cuadrada de 5 V que activa el relé de estado sólido (cerrando el circuito) en la posición alta y lo abre en la posición baja - Para este caso en particular, la frecuencia de la onda cuadrada no es importante. Sólo tiene que ser distinto de cero.
- Maximizar el DC offset (+ 5 V) en el generador de señal. Con esta configuración, el circuito siempre es cerrado y el sistema genera las burbujas continuamente.
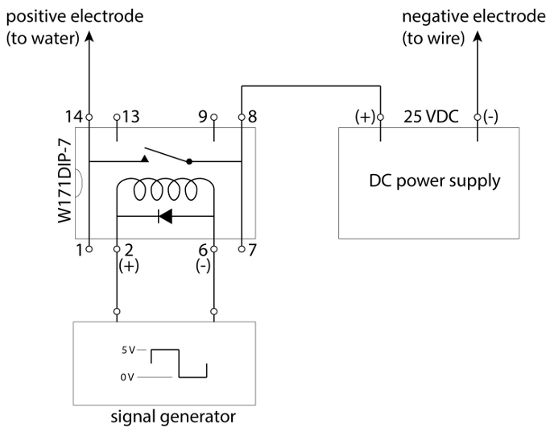
Figura 3. Diagrama de conexiones.

Figura 4. Sección de prueba. Flujo va de izquierda a derecha. El electrodo negativo genera una capa de burbujas de hidrógeno que son arrastrados por la corriente. El electrodo positivo se encuentra en el extremo aguas abajo de la sección de prueba para evitar que sus disturbios. Por favor haga clic aquí para ver una versión más grande de esta figura.
2. para producir líneas de tiempo:
- Gire en la facilidad de flujo
- Ajuste el disco del controlador de frecuencia a posición 2. Esto establecerá un caudal de aproximadamente 9 x 10-4 m3/s.
- Encienda la fuente de alimentación y aumentar el voltaje hasta unos 25 V, la corriente se fijó alrededor 190 mA.
- Establecer la forma de onda en el generador de señal a onda cuadrada (símbolo:
 ). Esto genera un 0 V - señal cuadrada de 5 V que activa el relé de estado sólido (cerrando el circuito) en la posición alta y desactivará (abrir el circuito) en la posición baja
). Esto genera un 0 V - señal cuadrada de 5 V que activa el relé de estado sólido (cerrando el circuito) en la posición alta y desactivará (abrir el circuito) en la posición baja - Establecer el desplazamiento DC en el generador de señal a + 1 V.
- Ajustar la frecuencia de la onda cuadrada en el generador de señal de 10 Hz.
- Establecer la simetría de la onda cuadrada ligeramente negativa (-2) para aumentar el espacio entre líneas de tiempo conservando la frecuencia correcta.
3. para utilizar líneas de flujo para el estudio de calle del vórtice de Von Kármàn:
- Medir el diámetro de la varilla,
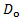 , utilizando un calibrador. Utilice las unidades S.I. para esta medida (m).
, utilizando un calibrador. Utilice las unidades S.I. para esta medida (m). - Fijar una varilla cilíndrica aguas abajo del electrodo negativo.
- Irradiemos la luz de la lámpara de descarga de alta intensidad en la capa de burbujas de hidrógeno. Asegúrese de que la luz no está directamente detrás de la línea de vista para evitar la sobresaturación del sistema de proyección de imagen
- Alinear el sistema de visualización con la barra; de manera que sólo la extremidad circular es visible delante de la cámara.
- Añadir una marca en la ventana de visualización y aguas abajo de la barra a utilizar como referencia para contar vortex-galpón ciclos por unidad de tiempo.
4. Análisis de datos para el flujo más allá de un cilindro circular:
- Determinación del factor de conversión de unidades de la máquina a las unidades de espacio real:
- Medir la anchura de la sombra de la varilla en la hoja de la burbuja (ver figura 2 para la referencia). Tomar la derecha de esta medida en la varilla para evitar la distorsión con la distancia. Este es el diámetro de la varilla en las unidades de la máquina,
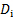 (puntos o píxeles, dependiendo del formato)
(puntos o píxeles, dependiendo del formato) - Utilice la siguiente ecuación para determinar el factor de conversión de unidades de la máquina a las unidades del mundo real:

- Medir la anchura de la sombra de la varilla en la hoja de la burbuja (ver figura 2 para la referencia). Tomar la derecha de esta medida en la varilla para evitar la distorsión con la distancia. Este es el diámetro de la varilla en las unidades de la máquina,
- Determinación de la velocidad de flujo:
- Escoger un grupo de plazos sin distorsión aguas arriba del cuerpo del pen # asco.
- Medir la distancia entre la primera y la última línea de tiempo en unidades de la máquina,
 (puntos o píxeles).
(puntos o píxeles). - Contar el número de líneas de tiempo en el grupo,
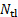 .
. - Tomar nota de la frecuencia de la señal de onda cuadrada como producidos por el generador de señal,
 .
. - Determinar la velocidad del flujo que se acerca de la siguiente ecuación:

- Determinación del número de Reynolds:
- Encontrar la viscosidad cinemática del fluido de trabajo (por ejemplo agua
 m2/s).
m2/s). - Calcular el número de Reynolds mediante la ecuación (1). Para ello, teniendo en cuenta el diámetro de la varilla (
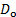 ) medido en el paso 3.1, la velocidad que se aproxima (
) medido en el paso 3.1, la velocidad que se aproxima ( ) determinada con la ecuación (5) y la viscosidad cinemática determinada en el paso 4.3.1
) determinada con la ecuación (5) y la viscosidad cinemática determinada en el paso 4.3.1
- Encontrar la viscosidad cinemática del fluido de trabajo (por ejemplo agua
- Determinación del número de Strouhal: los vórtices en la estela de la varilla están moviendo a una velocidad diferente como los plazos en la corriente libre. Por lo tanto, la frecuencia del vertimiento del vórtice debe estimarse independientemente.
- Definir una referencia fija aguas abajo de la barra. Esta referencia podría ser un hilo fino conectado al exterior del túnel o una línea digital a un video del proceso de flujo.
- Contar el número de ciclos, del vertimiento de vórtice
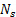 , cruzar la referencia durante un período definido de tiempo
, cruzar la referencia durante un período definido de tiempo  . Un vórtice vertimiento ciclo se ilustra en la figura 2(A).
. Un vórtice vertimiento ciclo se ilustra en la figura 2(A). - Calcular la frecuencia de desprendimiento de la siguiente ecuación:
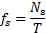
- Utilizar los resultados de las ecuaciones (5) y (6) en la ecuación (2) para calcular el número de Strouhal.
Resultados
La figura 2 muestra dos resultados representativos de la visualización de burbujas de hidrógeno de un vórtice de Von Kármàn calle. Figura 2 (A) muestra un ejemplo de un campo de línea como lo demuestran los disturbios en la hoja de la burbuja de hidrógeno. Esta imagen se utiliza para extraer el diámetro de la varilla en las unidades de la máquina. Figura 2 (B) se muestra un ejemplo de un campo de líneas de tiempo. Esta imagen se utiliza para estimar la velocidad del fluido que. Los parámetros extraídos de este particular experimento se resumen en la tabla 2.
Tabla 2 . Resultados representativos de flujo más allá de un cilindro circular.
| Parámetro | Valor |
| D_o | 0,003 m |
| D_i | 14,528 pts |
| f_s | 2.169 Hz |
| f_tl | 10 Hz |
| L | 130,167 "pts" |
| M | ∕ 4842,67 "pts" "m" |
| N_s | 60 |
| N_tl | 7 |
| T | 27.66 s |
| U_∞ | 0.0384 m/s |
| Ν | 1.004×[10]^(-6) m2/s |
| Re | 115 |
| St | 0.169 |
Puesto que el número de Reynolds es 115 para el presente ejemplo, se puede probar la validez de este resultado usando la ecuación (3) para
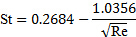 (7)
(7)
De la cual obtenemos:
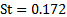 (8)
(8)
Después de comparar esta estimación con nuestra experimental resultado (ver tabla 2 para la referencia), podemos concluir que nuestro experimento ofrece un resultado satisfactorio. La figura 5 muestra un conjunto de resultados experimentales en comparación con las predicciones de la ecuación (7).

Figura 5 . Resultados experimentales. Comparación de resultados experimentales actuales contra las predicciones de la relación entre el número de Reynolds y el número de Strouhal de flujo más allá de un cilindro circular.
Aplicación y resumen
En este estudio, se demostró el uso de burbujas de hidrógeno para extraer información cualitativa y cuantitativa de las imágenes del flujo alrededor de un cilindro circular. La información cuantitativa extraída de estos experimentos incluye la velocidad de flujo libre ( ), frecuencia de vertimiento de vórtice (
), frecuencia de vertimiento de vórtice (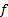 ), número de Reynolds (Re) y el número de Strouhal (St). En particular, los resultados de St vs Re exhibieron muy buen acuerdo con estudios previos [3].
), número de Reynolds (Re) y el número de Strouhal (St). En particular, los resultados de St vs Re exhibieron muy buen acuerdo con estudios previos [3].
Debido a la lenta velocidad utilizada en los experimentos actuales, las perturbaciones en la hoja de la burbuja producen una capa de burbujas entreverado. Estas rayas son básicamente línea. Como la hoja de la burbuja de hidrógeno viaja río abajo, esta línea espesa y más irregulares. Este es el resultado de la intensidad de turbulencia en la corriente libre. El efecto se atenúa según aumenta la velocidad del túnel ya que las burbujas dejan la sección de prueba antes de presentar una dispersión significativa. Línea puede también ser producido en lugares previamente seleccionados por el alambre de la capa dejando pequeñas partes expuestas al agua.
El actual comportamiento del flujo es directamente aplicable a fluir estructuras de ingeniería como los pilares de puentes y plataformas petroleras costa afuera, torres de aerogeneradores de viento, o energía postes de línea para nombrar unos pocos. Y de hecho, este comportamiento es exhibido por cuerpos faroles con geometrías que cilíndrico como rascacielos. Dado que vórtices generan interacciones fluido-estructura que hacen estructuras oscilar, sabiendo el vórtice vertimiento las frecuencias en el que se expondrá una estructura dada es crítico para su diseño. En ese sentido, el ingeniero tiene que asegurarse la frecuencia natural de la estructura no sea tal que resonará con el vórtice vertimiento frecuencia, porque ello conducirá inevitablemente al fracaso catastrófico de la estructura. Apropiado usar leyes [10] y las burbujas de hidrógeno en un túnel de agua, un ingeniero puede simular la interacción de flujo con una estructura antes de su construcción para asegurarse de que su diseño es seguro o para averiguar si necesita modificaciones.
Además de cuerpos del pen # asco, visualización de burbujas de hidrógeno es una herramienta muy poderosa para estudiar el flujo alrededor de cuerpos aerodinámicos como superficies de sustentación o cascos de la nave. Haciendo uso de líneas de flujo generadas con esta técnica, se puede determinar parámetros como el ángulo de ataque en que puesto se lleva a cabo, o incluso estimar las características de elevación basadas en la velocidad de flujo. Más importante aún, el patrón de la distorsión de líneas fluidas ayudará al ingeniero para optimizar su diseño.
Visualización de burbujas de hidrógeno no se limita a los flujos externos como el de arriba mencionado. Este método también puede utilizarse para observar el flujo a través de canales abiertos o sistemas completamente cerrados. En este último caso, las paredes tendrá que ser transparente para asegurar el acceso óptico. Por ejemplo, si uno está interesado en el diseño de un difusor de flujo para flujo sub-sonic, burbujas de hidrógeno pueden utilizarse para determinar geométricas y condiciones para que el difusor exhibirá inestabilidad y separación del flujo del flujo. En base a esas observaciones, el diseño se podría optimizarse experimentalmente para asegurar su correcto funcionamiento.
Referencias
- Zöllner, F. Leonardo da Vinci 1452-1519: sketches and drawings, Taschen, 2004.
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Adrian, Ronald J., and Jerry Westerweel. Particle Image Velocimetry. Cambridge University Press, 2011.
- Gerrard, J. H., The wakes of cylindrical bluff bodies at low Reynolds number, Phil. Trans. Roy. Soc. (London) Ser. A, Vol. 288, No. 1354, pp. 351-382 (1978)
- Coutanceau, M. and Bouard, R., Experimental determination of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow, J. Fluid Mech., Vol. 79, Part 2, pp. 231-256 (1977)
- Kovásznay, L. S. G., Hot-wire investigation of the wake behind cylinders at low Reynolds numbers, Proc. Roy. Soc. (London) Ser. A, Vol. 198, pp. 174-190 (1949)
- Fey, U., M. König, and H. Eckelmann. A new Strouhal-Reynolds-number relationship for the circular cylinder in the range
 . Physics of Fluids, 10(7):1547, 1998.
. Physics of Fluids, 10(7):1547, 1998. - Maas, H.-G., A. Grün, and D. Papantoniou. Particle Tracking in three dimensional turbulent flows - Part I: Photogrammetric determination of particle coordinates. Experiments in Fluids Vol. 15, pp. 133-146, 1993.
- Malik, N., T. Dracos, and D. Papantoniou Particle Tracking in three dimensional turbulent flows - Part II: Particle tracking. Experiments in Fluids Vol. 15, pp. 279-294, 1993.
- Tropea, C., A.L. Yarin, and J.F. Foss. Springer Handbook of Experimental Fluid Mechanics. Vol. 1. Springer Science & Business Media, 2007.
- Monaghan, J. J., and J. B. Kajtar. Leonardo da Vinci's turbulent tank in two dimensions. European Journal of Mechanics-B/Fluids. 44:1-9, 2014.
- Becker, H.A. Dimensionless parameters: theory and methodology. Wiley, 1976.
Saltar a...
Vídeos de esta colección:

Now Playing
Visualización de flujo más allá de un cuerpo no fuselado
Mechanical Engineering
11.9K Vistas

Flotabilidad y arrastre en cuerpos sumergidos
Mechanical Engineering
30.0K Vistas

Estabilidad de los buques flotantes
Mechanical Engineering
22.6K Vistas

Propulsión y empuje
Mechanical Engineering
21.7K Vistas

Redes de tuberías y pérdidas de presión
Mechanical Engineering
58.1K Vistas

Enfriamiento y ebullición
Mechanical Engineering
7.7K Vistas

Saltos hidráulicos
Mechanical Engineering
41.0K Vistas

Análisis del intercambiador de calor
Mechanical Engineering
28.0K Vistas

Introducción a la refrigeración
Mechanical Engineering
24.7K Vistas

Anemometría de hilo caliente
Mechanical Engineering
15.6K Vistas

Medición de flujos turbulentos
Mechanical Engineering
13.5K Vistas

Jet que inciden sobre una placa inclinada
Mechanical Engineering
10.7K Vistas

Enfoque de conservación de la energía para el análisis de sistemas
Mechanical Engineering
7.4K Vistas

Conservación de masa y mediciones de tasa de flujo
Mechanical Engineering
22.6K Vistas

Determinación de las fuerzas de impacto en una placa plana con el método del control del volumen
Mechanical Engineering
26.0K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados