Visualisation de l'écoulement après un corps non profilé

Source : Ricardo Mejia-Alvarez, Hussam Hikmat Jabbar et Mahmoud N. Abdullatif, département de génie mécanique, Michigan State University, East Lansing, MI

En raison du caractère non linéaire de ses lois dirigeants, un mouvement fluide induit des écoulements complexes. Comprendre la nature de ces modèles a fait l’objet d’un examen approfondi pendant des siècles. Bien que les ordinateurs personnels et les superordinateurs sont largement utilisés pour déduire des modèles d’écoulement de fluide, leurs capacités sont encore insuffisantes pour déterminer la viscosimétrie exacte pour des géométries complexes ou hautement inertiels flux (par exemple quelle impulsion domine résistance visqueuse). Dans cette optique, une multitude de techniques expérimentales pour faire flux motifs évidents ont été mis au point qui peut atteindre le débit outils inaccessibles aux théorique et computationnelle des régimes et des géométries.

Cette démonstration étudiera l’écoulement du fluide autour d’un corps de bluff. Un corps de bluff est un objet que, grâce à sa forme, causes séparé des flux sur la majeure partie de sa surface. Cette méthode diffère un corps profilé, comme une surface portante, qui est aligné dans le flux et provoque la séparation de l’écoulement. Le but de cette étude est d’utiliser les bulles d’hydrogène comme une méthode de visualisation des modèles d’écoulement. Les bulles d’hydrogène sont produits par électrolyse en utilisant une source d’alimentation CC en immergeant ses électrodes dans l’eau. Bulles d’hydrogène sont forment dans l’électrode négative, qui doit être un fil très fin pour que les bulles restent petits et suivre le mouvement du fluide plus efficacement. Cette méthode convient pour des écoulements laminaires stables et instables et est basée sur les lignes de flux de base qui décrivent la nature de l’écoulement autour des objets. [1-3]

Cet article se concentre sur la description de la mise en oeuvre de la technique, y compris des détails sur l’équipement et son installation. Ensuite, la technique est utilisée pour démontrer l’utilisation de deux des lignes de flux essentiel pour caractériser l’écoulement autour d’un cylindre circulaire. Ces lignes de flux sont utilisées pour estimer certains paramètres de débit importantes comme la vitesse d’écoulement et le nombre de Reynolds et de déterminer les modes d’écoulement.

Dans cette configuration, nous examinerons la fluidité de l’eau avec une vitesse uniforme (doublé la vitesse d’écoulement libre) approchant un cylindre circulaire (Figure 1). Selon les conditions d’écoulement caractérisée par le nombre de Reynolds, ce flux peut devenir instable et donner lieu à des vortex-jetant. Vortex effusion est typique du débit au-delà des organes bluff qui, par opposition aux organes simplifiées, pièce séparation de la couche limite sur une partie substantielle de leur surface. Cette séparation de la couche limite conduit à la formation de tourbillons derrière le corps qui pourrait éventuellement démonter périodiquement dans la foulée. Lorsque le détachement périodique a lieu, les tourbillons génèrent alternantes zones de basse pression derrière le corps qui pourraient devenir des charges résonantes si la fréquence de délestage coïncide avec la fréquence naturelle du corps. Ce vortex effusion de processus est appelé le « Von Kármàn vortex rue » (Figure 2). Ce motif répétitif des tourbillons qui tournoie est causé par la séparation de l’écoulement instable autour du corps de bluff et se produit à certaines gammes de nombre de Reynolds. Éviter ce scénario est d’une importance significative dans la conception des ouvrages d’art tels que les cheminées et les piliers de pont car il peut entraîner des dommages catastrophiques.

Figure 1 . Flux passé un cylindre circulaire. Schéma de configuration de base. Un flux homogène avec une vitesse un cylindre droit de diamètre s’approche dont l’axe de symétrie est perpendiculaire à la vitesse qui s’approche.

Le nombre de Reynolds est un paramètre sans dimension défini comme le rapport des forces d’inertie aux forces visqueuses :

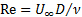(1)

Où 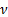est la viscosité cinématique du fluide, une vitesse caractéristique ( en l’espèce), et 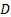au diamètre du cylindre. Le nombre de Reynolds est sans doute le paramètre le plus important dans la caractérisation des écoulements de fluides et sera utilisé tout au long de la présente expérience comme la métrique de l’émergence de la rue de vortex de Von Kármàn. En particulier, lorsque le nombre de Reynolds est autour de 5, l’écoulement présente deux tourbillons contra-rotatifs stables derrière le cylindre. Comme le nombre de Reynolds augmente, ces deux tourbillons s’allongent dans la direction de l’écoulement. Lorsque le nombre de Reynolds atteint une valeur d’environ 37, la suite devient instable et commence à osciller sinusoïdalement en raison d’un déséquilibre entre la pression et l’élan. Une nouvelle augmentation de nombre de Reynolds jusqu'à 47 provoque les deux tourbillons contra-rotatifs détacher la bouteille dans une séquence alternée qui suit l’oscillation sinusoïdale sillage [4,5,6].

La fréquence avec laquelle les tourbillons sont jeter hors du cylindre n’est pas constante ; Il varie avec la valeur du nombre de Reynolds. Délestage de fréquence se caractérise par le nombre de Strouhal, qui est l’autre paramètre sans dimension de pertinence dans cette configuration de l’écoulement du fluide particulier :

(2)

Ici, est la fréquence de délestage de vortex et les échelles de longueur et de vitesse sont les mêmes que pour le nombre de Reynolds. Vortex effusion fréquence peut alors être caractérisée par le nombre de Strouhal comme une fonction linéaire de la racine carrée inverse le nombre de Reynolds [7] :

(3)

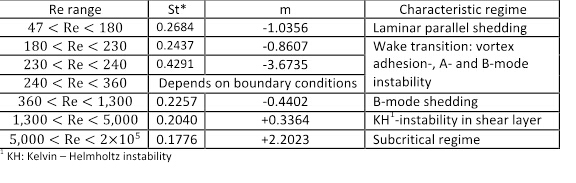
Cette fonction n’est pas toujours monotone, il présente des transitions supplémentaires à la suite des instabilités secondaires dues à la non-linéarité de l’écoulement du fluide. En conséquence, les coefficients de et 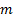changerait selon la gamme de nombre de Reynolds. Le tableau 1 montre les valeurs de ces coefficients pour les régimes d’écoulement qui ont été bien caractérisées dans la littérature [7].

Au cours de ces expériences, nous utiliserons des conduites d’écoulement afin d’étudier les flux externe autour d’un cylindre circulaire. Ces conduites d’écoulement sont définis comme suit :

• Pathline : chemin d’accès qui fait suite à une particule fluide comme il se déplace avec le courant.

• Streakline : locus continu de toutes les particules fluides dont le mouvement est née à la même localisation spatiale.

• Chronologie : ensemble de particules fluides qui ont été marqués à l’instant même du temps tout en formant un locus continu.

• Simplifiée : ligne continue qui est partout tangent vers le champ de vitesse à un instant dans le temps.

Les trois premières lignes sont relativement faciles à générer expérimentalement, tandis que les lignes de courant sont simplement un concept mathématique qui en général doivent être produits par une capture instantanée du champ vitesse de post-traitement. C’est toujours vrai, l’analyse simplifie considérablement en flux continus parce que courant, streaklines et rationalise coïncide avec l’autre. À l’inverse, ces lignes ne pas généralement coïncident avec l’autre flux instable. La mise en œuvre de cette technique est généralement simple et exige seulement faible coût matériel, par opposition à des techniques plus sophistiquées et coûteuses comme Particle Image Velocimetry [1], Particle Tracking Velocimetry [8,9] et le marquage moléculaire Vélocimétrie [10].

Figure 2 . Résultats représentatifs. (A) feuille continue de bulles d’hydrogène qui montre des streaklines à la suite des troubles en amont. L’ombre projetée par la tige est utilisée pour déterminer la conversion de la machine en unités réelles. Un vortex effusion cycle est aussi illustré pour aider à déterminer la fréquence de délestage convenablement. (B) un calendrier généré avec bulles d’hydrogène. Puisque la fréquence de la chronologie est bien définie, ils peuvent servir à mesurer la vitesse d’écoulement avec précision ; les délais entre les lignes rouges de comptage sera utilisé pour cette estimation. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Tableau 1 . Les valeurs des coefficients et pour différents Reynolds numéro intervalles (de [8]).

1. pour produire une feuille continue de bulles :

1. Réglez l’appareil conformément au schéma électrique illustré à la Figure 3.
2. Difficulté de l’électrode positive dans l’eau à l’extrémité aval de la section d’essai (pour référence, voir Figure 4 ).
3. Fixer l’électrode négative en amont et près du point d’intérêt de libérer les bulles dans le flux avant que le débit atteint l’objet d’étude (pour référence, voir Figure 4 ). L’eau remplit le circuit entre les deux électrodes.
4. Tourner à la facilité de circulation
5. Positionnez le cadran de la contrôleur de fréquence sur 2. Vous établirez un débit d’environ 9 x 10^-4 m3/s.
6. Allumez l’alimentation DC et augmenter la tension jusqu'à environ 25 V, le courant sera fixé environ 190 mA.
7. Définir la forme d’onde dans le générateur de signaux à onde carrée (symbole : 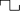). Ceci génère un 0 V - 5 signal carré V qui active le relais à semi-conducteurs (fermeture du circuit) en position haute et il ouvre en position basse
8. Pour ce cas précis, la fréquence de l’onde carrée n’est pas importante. Il a juste besoin d’être différent de zéro.
9. Maximiser l’offset DC (+ 5 V) dans le générateur de signaux. Avec ce paramètre, le circuit est toujours fermé et le système génère des bulles en continu.

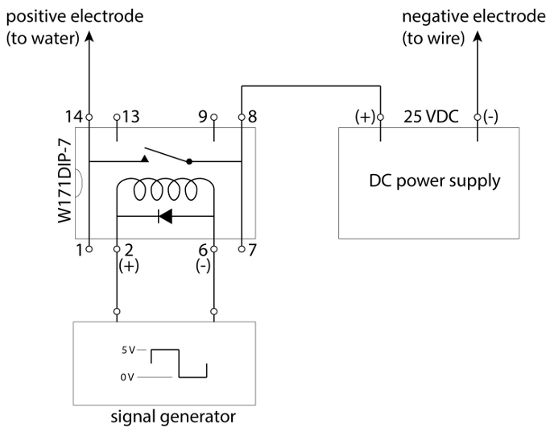
La figure 3. Schéma de connexions.

Figure 4. Section de l’essai. Débit allant de gauche à droite. L’électrode négative génère une couche de bulles d’hydrogène qui sont emportées avec l’écoulement. L’électrode positive est fixé à l’extrémité aval de la section test pour éviter les perturbations. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

2. pour produire un calendrier :

1. Tourner à la facilité de circulation
2. Positionnez le cadran de la contrôleur de fréquence sur 2. Vous établirez un débit d’environ 9 x 10^-4 m3/s.
3. Allumez l’alimentation DC et augmenter la tension jusqu'à environ 25 V, le courant sera fixé environ 190 mA.
4. Définir la forme d’onde dans le générateur de signaux à onde carrée (symbole : 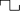). Cela génère un 0 V - 5 signal carré V qui active le relais à semi-conducteurs (fermeture du circuit) en position haute et désactive (l’ouverture du circuit) en position basse
5. Définir l’offset DC dans le générateur de signaux au + 1 V.
6. Définit la fréquence de l’onde carrée dans le générateur de signaux à 10 Hz.
7. Définissez la symétrie de l’onde carrée légèrement négative (-2) pour augmenter l’espace entre les délais tout en conservant la bonne fréquence.

3. d’utiliser les conduites d’écoulement pour étudier les rues vortex Von Kármàn :

1. Mesurer le diamètre de la tige,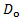, à l’aide d’un pied à coulisse. Utilisez les unités S.I. pour cette mesure (m).
2. Fixer une tige cylindrique en aval de l’électrode négative.
3. Monter la couche de bulles d’hydrogène à la lumière de la lampe à décharge haute intensité. Assurez-vous que la lumière n’est pas directement derrière de la ligne de vue pour éviter la sursaturation du système d’imagerie
4. Aligner le système de visualisation avec la tige ; d’une manière que seulement l’extrémité circulaire est visible devant la caméra.
5. Ajouter une marque dans la fenêtre de visualisation et en aval de la tige pour l’utiliser comme référence pour compter vortex-hangar cycles par unité de temps.

4. analyse des flux passé un cylindre circulaire :

1. Détermination du facteur de conversion des unités de machine aux unités de l’espace réel :
   1. Mesurez la largeur de l’ombre projetée par la tige sur la feuille de bulle (voir figure 2 a pour référence). Prendre cette mesure à droite à la tige pour éviter une distorsion avec la distance. C’est le diamètre de la tige en unités de machine, 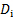(points ou pixels, en fonction du format)
   2. Utilisez l’équation suivante pour déterminer le facteur de conversion des unités de machine aux unités du monde réel :
      
2. Détermination de la vitesse d’écoulement :
   1. Choisissez un groupe de chronologies sans distorsion en amont du corps bluff.
   2. Mesurez la distance entre la première et la dernière chronologie en unités de machine, (points ou pixels).
   3. Compter le nombre d’échéances dans le groupe, .
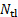   4. Prendre note de la fréquence du signal carré vague produite par le générateur de signaux, .
   5. Déterminer la vitesse d’écoulement qui s’approchait de l’équation suivante :
      
3. Déterminer le nombre de Reynolds :
   1. Trouver la viscosité cinématique du fluide de travail (p. ex. eaux m2/s).
   2. Calculer le nombre de Reynolds à l’aide de l’équation (1). Pour cela, compte tenu du diamètre de la tige (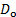) mesurée à l’étape 3.1, la vitesse d’approche () déterminé avec l’équation (5) et la viscosité cinématique déterminé à l’étape 4.3.1
4. Déterminer le nombre de Strouhal : Vortex dans le sillage de la tige se déplacent à une vitesse différente comme les échéances dans le flux libre. Par conséquent, la fréquence de l’excrétion de vortex doit être estimée de façon indépendante.
   1. Définir une référence fixe en aval de la tige. Cette référence pourrait être une ficelle fine fixée à l’extérieur du tunnel ou une ligne numérique ajouté à une vidéo du processus de flux.
   2. Compter le nombre de vortex effusion cycles, 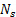, traversant la référence pendant une période définie de temps . Un vortex cycle de délestage est illustré à la Figure 2(A).
   3. Calculer la fréquence de délestage de l’équation suivante :
      
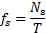
   4. Utiliser les résultats des équations (5) et (6) dans l’équation (2) pour calculer le nombre de Strouhal.

La figure 2 montre les deux résultats représentatifs de visualisation de bulles d’hydrogène d’un vortex de Von Kármàn rue. Figure 2 (A) montre un exemple d’un champ de streaklines comme en témoigne par des perturbations dans la feuille de bulles d’hydrogène. Cette image est utilisée pour extraire le diamètre de la tige en unités de machine. Figure 2 (B) montre un exemple d’un champ de chronologies. Cette image est utilisée pour estimer la vitesse du fluide qui s’en approchaient. Les paramètres tirés de cette expérience particulière sont résumées dans le tableau 2.

Tableau 2 . Les résultats représentatifs pour flux passé un cylindre circulaire.

Paramètre	Valeur
Concevoir	0,003 m
D_i	14,528 pts
f_s	2.169 Hz
f_tl	10 Hz
L	130,167 « pts »
M	∕ 4842,67 « pts » « m »
N_s	60
N_tl	7
T	27.66 s
U_∞	0.0384 m/s
Ν	1.004×[10]^(-6) m2/s
Re	115
St	0,169

Puisque le nombre de Reynolds est 115 pour l’exemple, la validité de ce résultat peut être testée en utilisant l’équation (3) pour

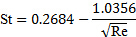(7)

D'où on obtient :

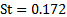(8)

Après avoir comparé cette estimation avec notre laboratoire résultat (voir tableau 2 pour référence), nous pouvons conclure que notre expérience offrait un résultat satisfaisant. La figure 5 présente un ensemble de résultats expérimentaux par rapport aux prédictions de l’équation (7).

Figure 5 . Résultats expérimentaux. Comparaison des résultats expérimentaux actuels contre les prédictions de la relation entre le nombre de Reynolds et le nombre de Strouhal pour flux passé un cylindre circulaire.

Dans cette étude, l’utilisation de bulles d’hydrogène a été démontrée pour extraire des informations qualitatives et quantitatives d’images de l’écoulement autour d’un cylindre circulaire. Les informations quantitatives extraites de ces expériences inclus la vitesse d’écoulement libre (), fréquence de délestage de vortex (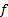), le nombre de Reynolds (Re) et le nombre de Strouhal (St). En particulier, les résultats pour St vs Re exposé très bon accord avec les études antérieures [3].

En raison de la vitesse lente utilisée dans les expériences actuelles, des perturbations dans la feuille de bulle produisent une couche de bulle entrelardées. Ces traînées sont essentiellement streaklines. Comme la feuille de bulles d’hydrogène se déplace en aval, ces streaklines s’épaissir et devenir plus irréguliers. C’est le résultat de l’intensité de la turbulence dans l’écoulement libre. L’effet est atténué lorsque la vitesse du tunnel augmente car les bulles sortent de la section d’essai avant de présenter une dispersion importante. Streaklines peut également être produit à lieux présélectionnés en enduisant le fil tout en laissant de petites parties de l’exposé à l’eau.

Le comportement actuel des flux est directement applicable aux flux passé d’ouvrages d’art tels que les piliers de ponts et de forage offshore, vent de tours d’éoliennes, ou alimenter des poteaux de ligne pour n’en nommer que quelques-uns. Et en fait, ce comportement est illustré par des organes bluff avec géométries autres que cylindriques comme les grattes ciel. Étant donné que les tourbillons de génèrent des interactions fluide-structure qui rendent les structures à osciller, sachant le vortex effusion de fréquences au cours de laquelle il s’exposera une structure donnée est essentielle pour sa conception. À cet égard, l’ingénieur doit s’assurer que la fréquence propre de la structure est pas telle qu’elle résonnera sur le vortex effusion de fréquence, car cet effet conduira inévitablement à l’échec catastrophique de la structure. À l’aide de l’échelle appropriée lois [10] et bulles d’hydrogène dans un tunnel d’eau, un ingénieur peut simuler l’interaction de débit avec une structure avant sa construction pour s’assurer que sa conception est sûre ou pour savoir si elle a besoin d’aucune modification.

En plus d’organismes bluff, visualisation de bulles d’hydrogène est un outil très puissant pour étudier les flux rationalisé corps tels que les profils aérodynamiques ou coques de navire. En faisant usage des lignes de flux générés avec cette technique, on peut déterminer les paramètres tels que l’angle d’attaque, à laquelle le décrochage a lieu, ou estiment même ascenseur caractéristiques basées sur la vitesse d’écoulement. Plus important encore, le patron de fausser le jeu de lignes fluides aidera l’ingénieur pour optimiser sa conception.

Visualisation avec bulles d’hydrogène n’est pas limitée aux flux extérieurs comme ci-dessus mentionné. Cette méthode permet aussi d’observer le flux par le biais de canaux ouverts ou systèmes d’écoulement entièrement clos. Dans ce dernier cas, les murs devront être transparent pour assurer l’accès optique. Par exemple, si l'on s’intéresse à la conception d’un diffuseur de flux pour débit partiel sonique, bulles d’hydrogène peuvent servir à déterminer géométrique et flux des conditions pour lesquelles le diffuseur exposera l’instabilité et la séparation de l’écoulement. Se fondant sur ces observations, la conception pourrait être expérimentalement optimisée afin d’assurer son bon fonctionnement.