קביעת כוחות מניעה על לוח שטוח בשיטת אמצעי האחסון של הפקד
Overview
מקור: ריקרדו מג'יה-אלווארז וחוסאם היקמט ג'באר, המחלקה להנדסת מכונות, אוניברסיטת מדינת מישיגן, מזרח לנסינג, MI
מטרת הניסוי היא להפגין כוחות על גופים כתוצאה משינויים בתנופה הלינארית של הזרימה סביבם באמצעות ניסוח נפח בקרה [1, 2]. ניתוח נפח הבקרה מתמקד בהשפעה המקרוסקופית של הזרימה על מערכות הנדסיות, ולא בתיאור המפורט שניתן להשיג בניתוח דיפרנציאלי. לכל אחת משתי הטכניקות הללו יש מקום בארגז הכלים של אנליסט הנדסה, ויש לראות בהן גישות משלימות ולא מתחרות. באופן כללי, ניתוח נפח בקרה ייתן למהנדס מושג על העומסים הדומיננטיים במערכת. זה ייתן לה / לו תחושה ראשונית על מה המסלול להמשיך בעת עיצוב מכשירים או מבנים, צריך להיות הצעד הראשוני לעשות באופן אידיאלי לפני רודף כל עיצוב מפורט או ניתוח באמצעות ניסוח דיפרנציאלי.
העיקרון העיקרי מאחורי ניסוח נפח הבקרה הוא להחליף את הפרטים של מערכת שנחשפה לזרימת נוזלים על ידי תרשים גוף חופשי פשוט יותר המוגדר על ידי משטח סגור דמיוני המכונה נפח הבקרה. תרשים זה צריך להכיל את כל כוחות פני השטח והגוף, את השטף נטו של תנופה ליניארית דרך גבולות נפח הבקרה, ואת קצב השינוי של תנופה ליניארית בתוך נפח הבקרה. גישה זו מרמזת על הגדרת נפח הבקרה בחוכמה בדרכים המפשטות את הניתוח בו זמנית הלוכדות את ההשפעות הדומיננטיות על המערכת. טכניקה זו תודגם עם מטוס סילון המעכב על צלחת שטוחה בזוויות שונות. אנו נשתמש בניתוח נפח בקרה כדי להעריך את העומס האווירודינמי על הצלחת, ונשווה את התוצאות שלנו למדידות בפועל של הכוח המתקבל עם איזון אווירודינמי.
Principles
אמצעי אחסון בקרה (CV) מוגדר על ידי משטח סגור דמיוני, המכונה משטח הבקרה (CS), המוגדר באופן שרירותי כדי לחקור את השפעת הזרימה סביב אובייקטים ומערכות. איור 1 מציג דוגמה לאמצעי אחסון של פקד המכיל אזור זרימה המסתובב סביב עצם מלא. הזרימה בסביבה הקרובה של האובייקט מורכבת ביותר, ואנו רוצים להימנע מהמורכבות הזו על מנת להעריך את ההשפעה הגלובלית של הזרימה על האלמנט התומך. לאחר שהוגדר, קורות חיים הופכים לדיאגרמת גוף חופשית הלוכדת את האינטראקציות בין הזרימה לאובייקט המצורף המעוררות עומסים במערכת התומכת. לשם כך, אנו משווים את פני השטח וכוחות הגוף בקופיות העיר עם שינוי התנופה הליניארית של הזרימה העוברת דרך קורות העיר. כוחות פני השטח הם לחץ, גיסת הנגרמת על ידי זרימה, וכל התגובות של מוצקים "לחתוך" על ידי נפח השליטה. כוחות הגוף הם בעצם המשקל של כל מה הכלול בנפח הבקרה, כולל מוצקים ונוזלים, וכל כוח אחר המושרה על ידי השפעות נפחיות כגון שדות אלקטרומגנטיים. השינוי בתנופה הלינארית של הזרימה הוא ההשפעה הנוספת של שטף התנח נטו דרך ה-CS וקצב שינוי המומנטום הכלול בקוה"ר. ניתן לסכם את כל ההשפעות הללו במשוואה לשימור המומנטום הליניארי בצורה אינטגרלית:
 (1)
(1)
הנה,  הם כוחות פני השטח והם כוחות
הם כוחות פני השטח והם כוחות  הגוף. המונח הראשון בצד ימין של המשוואה (1) מייצג את קצב שינוי המומנטום בתוך נפח הבקרה, בעוד המונח השני מייצג את שטף התנאם נטו דרך משטח הבקרה. ההבדל
הגוף. המונח הראשון בצד ימין של המשוואה (1) מייצג את קצב שינוי המומנטום בתוך נפח הבקרה, בעוד המונח השני מייצג את שטף התנאם נטו דרך משטח הבקרה. ההבדל  הווקטורי הוא המהירות היחסית בין קורות החיים לזרימה, והווקטור
הווקטורי הוא המהירות היחסית בין קורות החיים לזרימה, והווקטור  הוא היחידה הנורמלית כלפי חוץ להפרש האזור. המכפלה המנוקדת בין המהירות היחסית
הוא היחידה הנורמלית כלפי חוץ להפרש האזור. המכפלה המנוקדת בין המהירות היחסית  מייצגת את רכיב המהירות שחוצה את ה-CS, ומכאן ואילך תורמת לחילופי המומנטום הליניארי. הסימן של מוצר נקודה זה הוא שלילי שבו שטף המומנטום מופנה לקופות העיר וחיוביים שם הוא מופנה הרחק מהקו.וי. בצורה זו, משוואה (1) היא האיזון של מומנטום ליניארי ביחס למסגרת הפניה אינרציאלית. שים לב כי (1) היא משוואה וקטורית, כלומר באופן כללי יש שלושה רכיבים עצמאיים. עם זאת, האנליסט צריך להיות זהיר בהקמת מערכת הכוחות המאזנים שינויים בתנופה ליניארית עבור כל קואורדינטות.
מייצגת את רכיב המהירות שחוצה את ה-CS, ומכאן ואילך תורמת לחילופי המומנטום הליניארי. הסימן של מוצר נקודה זה הוא שלילי שבו שטף המומנטום מופנה לקופות העיר וחיוביים שם הוא מופנה הרחק מהקו.וי. בצורה זו, משוואה (1) היא האיזון של מומנטום ליניארי ביחס למסגרת הפניה אינרציאלית. שים לב כי (1) היא משוואה וקטורית, כלומר באופן כללי יש שלושה רכיבים עצמאיים. עם זאת, האנליסט צריך להיות זהיר בהקמת מערכת הכוחות המאזנים שינויים בתנופה ליניארית עבור כל קואורדינטות.
להדגמה הנוכחית, יש לנו את התצורה המוצגת באיור 1, שבו קורות קורות רישוי קבועים מקיפים לוחית שנחשפת למטוס סילון. מכיוון שזרימת הסילון יציבה, אין שינוי בתנופה בתוך קורות המים, כך שהמונח הראשון בצד ימין של המשוואה (1) נעלם. כמו כן, קורות העיר לא זזים, אז  . לפיכך, סיכום הכוחות על קורות העיר מאזן עם השטף נטו של מומנטום דרך ה- CS.
. לפיכך, סיכום הכוחות על קורות העיר מאזן עם השטף נטו של מומנטום דרך ה- CS.
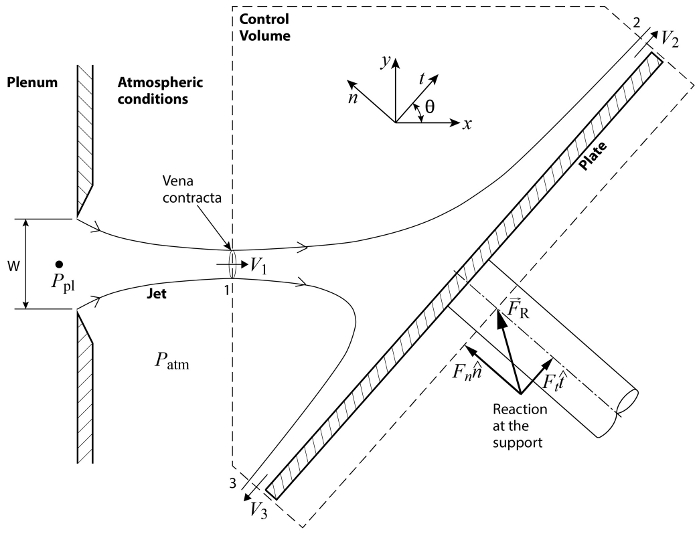
איור 1. סכמטי של תצורה בסיסית. מטוס סילון יוצא מהמליאה דרך חריץ ברוחב W. הסילון פוגע בלוח נוטה והוא מסיט אותו תוך הפעלת עומס על פני השטח.
בהתחשב בתצורה באיור 1, התנף זורם לקורתות העיר דרך יציאה 1 ומשאיר את קורות העיר דרך יציאות 2 ו-3. קורות חיים חוצה את המטוס הנכנס ב vena contracta, (לקבלת מידע נוסף, אנא ראה וידאו "משחק הגומלין של לחץ ומהירות: סילון פגיעה על צלחת נוטה") שהוא המקום הראשון שבו היעילות הופכות מקבילות, וכתוצאה מכך, הלחץ הסטטי על פני המטוס הופך הומוגני ומתאים את הערך של הלחץ שמסביב, כלומר, לחץ אטמוספרי  . באופן דומה, נמלים 2 ו -3 ממוקמים רחוק מספיק מהאזור המעכב כדי לאפשר לייעול להפוך למקבילים והלחץ להתאים לזה של הסביבה. כתוצאה מכך, הלחץ בכל מקום על ה- CS שווה ללחץ האטמוספרי,
. באופן דומה, נמלים 2 ו -3 ממוקמים רחוק מספיק מהאזור המעכב כדי לאפשר לייעול להפוך למקבילים והלחץ להתאים לזה של הסביבה. כתוצאה מכך, הלחץ בכל מקום על ה- CS שווה ללחץ האטמוספרי,  . כתוצאה מכך, בהתחשב בכך שהלחץ מופץ באופן הומוגני סביב ה- CS, כוח הנטו שלו בנפח הבקרה הוא אפס. בנוסף, מכיוון שה-CS נמשך בניצב לזרימות המפרצון והשקע, אין עומס גיסת שנגרם על ידי הזרימה על ה- CS. לסיכום, המשוואה (1) מפשטת את הקשר הבא עבור האירוע המומחשה באיור 1
. כתוצאה מכך, בהתחשב בכך שהלחץ מופץ באופן הומוגני סביב ה- CS, כוח הנטו שלו בנפח הבקרה הוא אפס. בנוסף, מכיוון שה-CS נמשך בניצב לזרימות המפרצון והשקע, אין עומס גיסת שנגרם על ידי הזרימה על ה- CS. לסיכום, המשוואה (1) מפשטת את הקשר הבא עבור האירוע המומחשה באיור 1
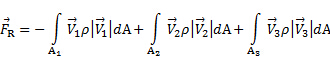 (2)
(2)
הנה,  התגובה של המערכת התומכת הנובעת משידור הטעינה האווירודינמית שהמטוס מפעיל על הצלחת. כפי שמוצג באיור 1, תגובה זו ממוקמת בחלק של נפח הבקרה ש"חותך" דרך המערכת התומכת של הצלחת. זה נחשב לכוח שטח במובן זה שהחתך הדמיוני הזה יהיה חלק משטח הבקרה. מכיוון
התגובה של המערכת התומכת הנובעת משידור הטעינה האווירודינמית שהמטוס מפעיל על הצלחת. כפי שמוצג באיור 1, תגובה זו ממוקמת בחלק של נפח הבקרה ש"חותך" דרך המערכת התומכת של הצלחת. זה נחשב לכוח שטח במובן זה שהחתך הדמיוני הזה יהיה חלק משטח הבקרה. מכיוון  שהאינטראקציה היחידה עם נפח השליטה אינה קשורה לשטף מומנטום, זהו המונח היחיד בצד שמאל של משוואות (1) ו -(2). שימו לב מהשוואת משוואות אלה זו לזו שמוצרי הנקודות בתוך האינטגרלים גורמים פשוט בסדרי הגודל של וקטור המהירות המתאימים מכיוון שהם מיושרים עם וקטורי האזור. כמו כן, כאמור, השלט שלהם אומר אם שטף המומנטום מופנה לקורה(-) או הרחק ממנו (+). אם נניח עוד כי המהירות בנמלים היא הומוגנית בקירוב, וכי הזרימה אינה ניתנת לריסון, ניתן לקחת את המהירויות והצפיפות מחוץ לאינטגרלים והמשוואה (2) הופכת:
שהאינטראקציה היחידה עם נפח השליטה אינה קשורה לשטף מומנטום, זהו המונח היחיד בצד שמאל של משוואות (1) ו -(2). שימו לב מהשוואת משוואות אלה זו לזו שמוצרי הנקודות בתוך האינטגרלים גורמים פשוט בסדרי הגודל של וקטור המהירות המתאימים מכיוון שהם מיושרים עם וקטורי האזור. כמו כן, כאמור, השלט שלהם אומר אם שטף המומנטום מופנה לקורה(-) או הרחק ממנו (+). אם נניח עוד כי המהירות בנמלים היא הומוגנית בקירוב, וכי הזרימה אינה ניתנת לריסון, ניתן לקחת את המהירויות והצפיפות מחוץ לאינטגרלים והמשוואה (2) הופכת:
 (3)
(3)
באופן קפדני, פרופיל המהירות הוא אף פעם לא הומוגני לחלוטין, ופישוט זה דורש כפל על ידי מקדם תיקון,  אשר הערך תלוי בפרטי פרופיל המהירות. ביציאת שטף נתונה, מקדם זה מוגדר כיחס בין שטף התנעה המדויק לבין שטף התנעה המוערך מהמהירות הממוצעת:
אשר הערך תלוי בפרטי פרופיל המהירות. ביציאת שטף נתונה, מקדם זה מוגדר כיחס בין שטף התנעה המדויק לבין שטף התנעה המוערך מהמהירות הממוצעת:
 (4)
(4)
בזרימות סוערות מקדם זה קרוב מאוד ל- 1 מכיוון שפרופיל המהירות נוטה להיות קרוב להומוגני. מכיוון שזה המקרה לניסוי הנוכחי, משוואה (3) היא קירוב סביר למדידות הנוכחיות. אבל אם קצב הזרימה יופחת או המיקום של הלוח נע רחוק יותר במורד הזרם עד להגיע לתנאי זרימת למינאר, יהיה צורך לפתור את האינטגרלים בצד ימין של המשוואה (2) ללא קירוב. בהתבסס על איור 1,  ניתן לפרק את הקואורדינטות הרגילות והמשויקות שלו לצלחת
ניתן לפרק את הקואורדינטות הרגילות והמשויקות שלו לצלחת  . איפה
. איפה 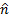
 וקטורי היחידה בכל קואורדינטות
וקטורי היחידה בכל קואורדינטות 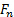
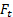 והם סדרי הגודל של התחזיות של
והם סדרי הגודל של התחזיות של  בכל קואורדינטות. לפיכך, ניתן לרקיב את המשוואה (3) כ:
בכל קואורדינטות. לפיכך, ניתן לרקיב את המשוואה (3) כ:
 (5)
(5)
שים לב שסימן החיסור ברכיב הרגיל נעלם מכיוון שההקרנה של  על הציר הרגיל היא שלילית. אנחנו רוצים לקבוע את העומס הרגיל על הצלחת עם מחקר זה כי זה נוטה להיות המרכיב הרלוונטי ביותר מנקודת המבט המבנית. מתוך משוואה (4), אנו מקבלים את העומס הרגיל על הצלחת:
על הציר הרגיל היא שלילית. אנחנו רוצים לקבוע את העומס הרגיל על הצלחת עם מחקר זה כי זה נוטה להיות המרכיב הרלוונטי ביותר מנקודת המבט המבנית. מתוך משוואה (4), אנו מקבלים את העומס הרגיל על הצלחת:
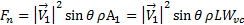 (6)
(6)
הנה, 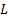 הוא טווח הצלחת והוא רוחב המטוס על
הוא טווח הצלחת והוא רוחב המטוס על 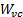 כווץ vena. באופן כללי, יחס ההתכווצות בין רוחב יציאת הסילון לבין
כווץ vena. באופן כללי, יחס ההתכווצות בין רוחב יציאת הסילון לבין  החוזה של הווניל קרוב מאוד ל- [2, 3, 4]:
החוזה של הווניל קרוב מאוד ל- [2, 3, 4]:
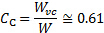 (7)
(7)
לסיכום, ניתן להעריך את הכוח הנורמלי על הצלחת ממערכת היחסים הבאה:
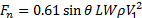 (8)
(8)
כאן, אנו  מגדירים לפשטות. מאידך גיסא, ערך המונח
מגדירים לפשטות. מאידך גיסא, ערך המונח  נקבע באמצעות משוואת ברנולי בין המליאה לוונקה (ראו איור 2 לעיון). המהירות בתוך המליאה נחשבת זניחה, ובהתחשב בכך שהמטוס אופקי, שינויים בגובה בין המליאה לוועידה נעלמים. לפיכך, המשוואה של ברנולי הופכת:
נקבע באמצעות משוואת ברנולי בין המליאה לוונקה (ראו איור 2 לעיון). המהירות בתוך המליאה נחשבת זניחה, ובהתחשב בכך שהמטוס אופקי, שינויים בגובה בין המליאה לוועידה נעלמים. לפיכך, המשוואה של ברנולי הופכת:
 (9)
(9)
נזכיר כי הלחץ על החוזה של הווניל תואם את הלחץ שמסביב, שהוא אטמוספרי. לפיכך, הלחץ הדינמי על החוזה vena כדלקמן:
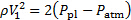 (10)
(10)
החלפת משוואת (9) במשוואה (7) נותנת את התוצאה הסופית להערכת הכוח הנורמלי על הלוח בהתבסס על המאפיינים של מטוס המטוס:
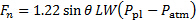 (11)
(11)
תוצאה זו נובעת מניתוח נפח הבקרה של שימור המומנטום הליניארי. כדי שתהיה הערכה של דיוקו, נשווה את ההערכות הללו למדידות ישירות של הכוח. עד לסוף זה, הרכיבים האופקיים ( 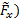 והאנכיים )
והאנכיים )  של הכוח הכולל המתואר באיור 2 נלכדים על-ידי איזון אווירודינמי. כדי לקבוע את הרכיבים של כוח מדוד זה
של הכוח הכולל המתואר באיור 2 נלכדים על-ידי איזון אווירודינמי. כדי לקבוע את הרכיבים של כוח מדוד זה  במערכת הקואורדינטות, אנו משתמשים בטרנספורמציה הקואורדינטת הבאה:
במערכת הקואורדינטות, אנו משתמשים בטרנספורמציה הקואורדינטת הבאה:
 (12)
(12)
 (13)
(13)
שם נוספה אריחה כדי להדגיש כי כוחות אלה מתקבלים על ידי מדידה ישירה עם איזון אווירודינמי.
Procedure
1. הגדרת המתקן
- ודא שאין זרימה במתקן.
- חבר את היציאה החיובית של מתמר הלחץ לברז הלחץ של המליאה (
 ).
). - השאר את היציאה השלילית של מתמר הלחץ פתוח לאטמוספירה (
 ).
). - הקלט את גורם ההמרה של המתמר מוולט לפסקל (
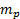 ).
). - הקלט את רוחב יציאת הסילון.
- הקלט את טווח הצלחת.
- הקלט את קבועי ההמרה של מאזן הכוח מוולט לניוטון (כוח אופקי:
 ; כוח אנכי:
; כוח אנכי:  ).
). - הגדר את מערכת רכישת הנתונים לדוגמה בקצב של 100 הרץ עבור סך של 1000 דוגמאות (כלומר 10s של נתונים).
- הר את לוח ההשפעה על מאזן הכוח והתאם את התפוקות שלו לאפס.
2. הקלטת הנתונים
- הגדר את זווית הצלחת ל- 90o (ראו איור 2 לעיון).
- הפעל את מתקן הזרימה.
- הקלט את קריאת מתמר הלחץ בוולט, התואם את הפרש הלחץ בין המליאה לאטמוספירה (
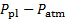 ).
). - הקלט את נתוני הכוח באמצעות מערכת רכישת הנתונים.
- הכפל את הערכים שנרכשו (ב- Volts) בגורמי המרת הכוח (

 ו) והזן את התוצאות בטבלה 1.
ו) והזן את התוצאות בטבלה 1. - כבה את מתקן הזרימה.
- שנה את זווית הצלחת.
- חזור על שלבים 2.2 עד 2.6 עבור הזוויות הבאות:
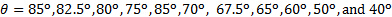

איור 2 . הגדרה ניסיונית. (A): פירוט של מערכת צריכת לחץ על המליאה בלחץ  . (B): צד פריקה עם צלחת מכשולים. (ג): פרט של חריץ פריקה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
. (B): צד פריקה עם צלחת מכשולים. (ג): פרט של חריץ פריקה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
3. ניתוח נתונים
- חשב את הכוח הנורמלי הנמדד לפי היתרה באמצעות משוואות(11) ורשום אותה בטבלה 1.
- קבע את הערך התיאורטי של הכוח הנורמלי מהמשוואה (10) ורשום אותו בטבלה 1.
- חשב את המחלוקת בין שני הערכים כאחוז.
טבלה 1. פרמטרים בסיסיים למחקר ניסיוני.
| פרמטר | ערך |
| רוחב זרבובית סילון (W) | 19.05 מ"מ |
| טווח צלחת (L) | 110.49 ס"מ |
| קבוע כיול מתמר (m_p) | 141.3829 אבא/וי |
| מקדם אופקי איזון (m_x) | 22.2411 N/V |
| מקדם אנכי איזון (m_y) | 4.4482 נ"ל/V |
Results
איור 3 מראה השוואה בין העומס הרגיל על הלוח השטוח כפי שהוא נמדד ישירות מאיזון אווירודינמי ומוערך משימור המומנטום הליניארי. באופן כללי, ניתוח המומנטום הליניארי לכד את הנטייה הדומיננטית של מדידות ישירות כאשר זווית ההסתבכות משתנה. הפערים במדידות אלה השתנו באופן לא מונוטוני עם זווית ההפגיעה. עבור זוויות מכשולים בטווח 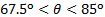 , ועל ,
, ועל ,  פערים הם מתחת 6%. הם גבוהים יותר עבור הזוויות האחרות, אך אף פעם לא גבוהים מ-12.5%. נראה שיש קרוסאובר סביב
פערים הם מתחת 6%. הם גבוהים יותר עבור הזוויות האחרות, אך אף פעם לא גבוהים מ-12.5%. נראה שיש קרוסאובר סביב 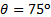 , שבו הנטייה של פערים הפוכה: מדידות להפגין עומסים נורמליים גבוהים יותר מאשר ניתוח של מומנטום ליניארי
, שבו הנטייה של פערים הפוכה: מדידות להפגין עומסים נורמליים גבוהים יותר מאשר ניתוח של מומנטום ליניארי  עבור ונמוך עבור
עבור ונמוך עבור 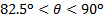 . הבדלים אלה בנטיות עשויים להיות בשל העובדה כי ניתוח של מומנטום ליניארי מניח שינויים בלתי פוסקים, לא מתפזרים, בתנופה ליניארית, בעוד מדידות ישירות לא יכול למנוע את ההשפעה של צמיגות על הזרימה. עבור הטווח
. הבדלים אלה בנטיות עשויים להיות בשל העובדה כי ניתוח של מומנטום ליניארי מניח שינויים בלתי פוסקים, לא מתפזרים, בתנופה ליניארית, בעוד מדידות ישירות לא יכול למנוע את ההשפעה של צמיגות על הזרימה. עבור הטווח  , רכיב הגיסה הופך דומיננטי ולכן אפקטים שכבת גבול סוערת יכול להיות חשוב. במקרה זה, תנודות מהירות קיר נורמלית עקב מערבולת עשוי להיות אחראי לעלייה בעומס הרגיל. מצד שני, המהירות צירית של המטוס חווה ירידה משמעותית בטווח
, רכיב הגיסה הופך דומיננטי ולכן אפקטים שכבת גבול סוערת יכול להיות חשוב. במקרה זה, תנודות מהירות קיר נורמלית עקב מערבולת עשוי להיות אחראי לעלייה בעומס הרגיל. מצד שני, המהירות צירית של המטוס חווה ירידה משמעותית בטווח 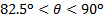 בעוד הוא הופך להיות משיק דומיננטי לקיר. השפעה זו צפויה לאפשר לצמיגות לפזרים צמיגות עקב ירידה בערכים המקומיים של מספר ריינולדס, וזה יגרום לערכים מופחתים של העומס הרגיל.
בעוד הוא הופך להיות משיק דומיננטי לקיר. השפעה זו צפויה לאפשר לצמיגות לפזרים צמיגות עקב ירידה בערכים המקומיים של מספר ריינולדס, וזה יגרום לערכים מופחתים של העומס הרגיל.
טבלה 2. תוצאות מייצגות.
| θ | F ̃_x(N) | F ̃_y (N) | F ̃_n (N) | F_n (N) | ε (%) |
| 90o | 15.257 | 9.034 | 15.257 | 16.773 | 9.9 |
| 85o | 15.151 | 9.831 | 15.950 | 16.709 | 4.8 |
| 82.5o | 15.035 | 10.231 | 16.242 | 16.630 | 2.4 |
| 80o | 15.929 | 10.498 | 17.510 | 16.518 | 5.7 |
| 75o | 14.248 | 10.453 | 16.468 | 16.202 | 1.6 |
| 70o | 13.518 | 11.405 | 16.604 | 15.762 | 5.1 |
| 67.5o | 13.100 | 11.294 | 16.425 | 15.496 | 5.7 |
| 65o | 12.771 | 11.579 | 16.468 | 15.202 | 7.7 |
| 60o | 11.881 | 11.863 | 16.221 | 14.526 | 10.5 |
| 50o | 9.746 | 11.241 | 14.691 | 12.849 | 12.5 |
| 40o | 6.357 | 9.444 | 11.320 | 10.782 | 4.8 |
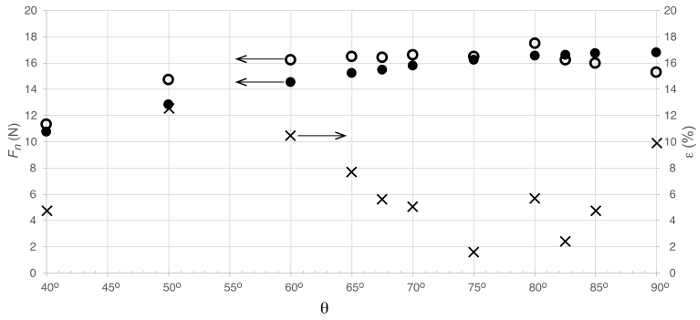
איור 3. תוצאות מייצגות. טען על צלחת כתוצאה של סילון פוגע. הסמלים מייצגים:  : מדידת עומס ישיר;
: מדידת עומס ישיר;  הערכה משימור התנח הליניארי;
הערכה משימור התנח הליניארי;  אחוז טעות בין מדידות ניסיוניות להערכה תיאורטית.:
אחוז טעות בין מדידות ניסיוניות להערכה תיאורטית.:
Application and Summary
הדגמנו את היישום של ניתוח נפח בקרה של שימור תנופה ליניארית כדי לקבוע את הכוחות המופעלים על ידי מטוס פוגע על צלחת שטוחה. ניתוח זה הוכח פשוט ליישם, ונתן הערכה בתפזורת משביעת רצון של עומסים ללא צורך ידע מפורט של דפוס הזרימה סביב הצלחת. למרות שהיו כמה פערים (הן בסדר גודל והן בנטייה) בשל ההנחה הבסיסית של טרנספורמציה בלתי נראה של מומנטום, טכניקה זו מציעה אמצעי להשגת הערכה מהירה של התנהגות המערכת מבלי להתעמק במחקר מפורט של זרימת נוזלים. לפיכך, זהו כלי רב עוצמה עבור האנליסט ההנדסי, למשל, לחזות את ההיתכנות של פיתוח מערכת הנדסית נתונה עם השקעה מינימלית של זמן ומשאבים. לאחר ניתוח ראשון זה נערך כדי לקבוע היתכנות, המהנדס יכול לעבור לניתוח זרימה מפורט יותר באמצעות, למשל, דינמיקת נוזל חישובי.
ניתוח נפח בקרה של שימור מומנטום ליניארי הוא כלי רב עוצמה להנדסת נוזלים. הוא מוצא יישום במגוון רחב של בעיות כדי לעקוף שיטות מעורבות יותר כגון ניתוח דיפרנציאלי. ניתן לתאר מספר מקרים של ניתוח זה:
עיצוב להב טורבינת פלטון: באופן כללי, להב טורבינה פלטון צריך להיות מתוכנן להמיר את הכמות הגבוהה ביותר של מומנט ליניארי למומנט. זה מושג על ידי קביעת הגיאומטריה של הלהב שממקסם את השינוי בתנופה הליניארית של סילוני מים. לכך, התוצאה האופיינית של ניתוח נפח הבקרה היא כי המטוס צריך להיעשות להסתובב על עצמו, כלומר, 180o. זהו באופן כללי אתגר טכני עבור מכשיר מסתובב, אך נותן לאנליסט הדרכה ראשונית לניתוח מפורט יותר באמצעות כלים אחרים.
עומס גרירה על מבנים אזרחיים: אחד האתגרים של הנדסה אזרחית הוא לתכנן מבנים העומדים בעומס הרוח. על מנת לחזות את השפעות הרוח על מבנה בגודל אמיתי, ניתן לערוך ניסויים במודל בקנה מידה כלפי מטה במנהרות רוח או מים. לכך, ניתן להשתמש בניתוח נפח בקרה של שימור תנופה ליניארית בהתבסס על מדידות מהירות במעלה ובמורד הזרם של המודל כדי לקבוע את העומס האפקטיבי על אב הטיפוס. שיטה זו מפשטת את הקמפיין הניסיוני וחוסכת זמן, מאמץ וכסף כהכנה לבניית מבנה בקנה מידה אמיתי.
References
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
- Buckingham, E. Note on contraction coefficients of jets of gas. Journal of Research,6:765-775, 1931.
- Lienhard V, J.H. and J.H. Lienhard IV. Velocity coefficients for free jets from sharp-edged orifices. ASME Journal of Fluids Engineering, 106:13-17, 1984.
Skip to...
Videos from this collection:

Now Playing
קביעת כוחות מניעה על לוח שטוח בשיטת אמצעי האחסון של הפקד
Mechanical Engineering
26.0K Views

ציפה וגרירה על גופים שקועים
Mechanical Engineering
30.2K Views

יציבות של כלי שיט צפים
Mechanical Engineering
22.8K Views

הנעה ודחף
Mechanical Engineering
21.9K Views

רשתות צנרת והפסדי לחץ
Mechanical Engineering
58.6K Views

מרווה ומרתיח
Mechanical Engineering
7.9K Views

קפיצות הידראוליות
Mechanical Engineering
41.1K Views

ניתוח מחליף חום
Mechanical Engineering
28.2K Views

מבוא לקירור
Mechanical Engineering
24.9K Views

שושנת ים של חוט חם
Mechanical Engineering
15.8K Views

מדידת זרמים סוערים
Mechanical Engineering
13.6K Views

הדמיה של זרימה בעבר גוף בלוף
Mechanical Engineering
12.0K Views

ג'ט פוגע בלוח נוטה
Mechanical Engineering
10.8K Views

שימור הגישה האנרגטית לניתוח מערכות
Mechanical Engineering
7.4K Views

מדידות של שימור המוני וקצב זרימה
Mechanical Engineering
22.9K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved