Conservation de la masse et mesures de débit

Source : Ricardo Mejia-Alvarez et Hussam Hikmat Jabbar, département de génie mécanique, Michigan State University, East Lansing, MI

Le but de cette expérience est de démontrer l’étalonnage d’un passage de flux, comme un débitmètre à l’aide d’une formulation de volume (CV) de contrôle [1, 2]. L’analyse de CV se concentre sur l’effet macroscopique du courant sur l’ingénierie des systèmes, plutôt que la description détaillée qui pourrait être obtenue avec une analyse détaillée du différentielle. Ces deux techniques doivent envisager des approches complémentaires, comme l’analyse de CV donnera à l’ingénieur une base initiale sur quelle voie poursuivre lors de la conception d’un système d’écoulement. Grosso modo, une analyse de CV donnera l’ingénieur une idée de l’échange de masse dominante dans un système et devrait idéalement être la première étape à prendre avant de poursuivre toute conception détaillée ou analyse par formulation différentielle.

Le principe derrière l’élaboration de CV pour la conservation de la masse est de remplacer les détails d’un système de flux par un volume simplifié enfermé dans ce qu’on appelle la surface de contrôle (CS). Ce concept est imaginaire et peut être définis librement pour habilement simplifier l’analyse. Par exemple, le CS devrait « cut » des orifices d’entrée et de sortie dans une direction perpendiculaire à la vitesse de la dominante. Ensuite, l’analyse consisterait à trouver l’équilibre entre le flux net de masse par le CS et le taux de variation de la masse à l’intérieur du CV. Cette technique sera démontrée avec l’étalonnage d’une contraction lisse comme un débitmètre.

Un volume de contrôle (CV) est défini par une surface fermée imaginaire, surnommée la surface de contrôle (CS), définie arbitrairement afin d’étudier l’équilibre de la masse dans un système. Figure 1 a montre un exemple d’un volume de contrôle contenant une région de débit en passant par un passage de flux. Les détails du flux dans le passage ne sont pas pertinents puisque nous sommes seulement intéressés à obtenir des mesures de la masse entrées, sorties et son taux de variation à l’intérieur du passage de l’écoulement. Tous ces effets peuvent se résumer dans l’équation de conservation de la masse en forme intégrale [1, 2] :

(1)

Le premier terme à droite de l’équation (1) représente le taux de variation de la masse à l’intérieur du volume de contrôle, tandis que le second terme représente le flux net de masse à travers la surface de contrôle. La différence de vecteur 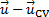est la vitesse relative entre le CV et le flux et le vecteur est l’unité vers l’extérieur normaux à la superficie différentielle. Le produit scalaire entre la vitesse relative et représente la composante de vitesse qui traverse le CS et désormais contribue à l’échange de masse. Le signe de ce produit scalaire est négatif lorsque le flux de masse est dirigé dans le CV et positif où il est dirigé loin de la CV.

Figure 1. SCweek-ends de configuration de base. (A) bon apport pour un ventilateur centrifuge. Le volume de contrôle est défini comme l’intérieur profil du passage. Les murs massifs sont exclus le volume de contrôle, mais leurs conditions aux limites sont conservées dans la surface de contrôle (pas de pénétration et aucun feuillet). Port 1 est défini comme du côté de l’entrée du passage, tandis que le port 2 est défini comme l’avion transversale qui coïncide avec l’extrémité du tube de Pitot. Débit allant de gauche à droite. B système Pitot-statique et schematic du système d’acquisition de données. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Pour la démonstration actuelle, nous avons les configurations illustrées à la Figure 1 a, où un CV fixe suit le contour de la contraction lisse à l’apport d’un ventilateur centrifuge. Le débit à travers ce CV est constant, donc le taux de variation de la masse à l’intérieur du volume de contrôle est égale à zéro. Par conséquent, le premier terme à droite de l’équation (1) disparaît. En outre, le CV est attaché à la contraction, ce qui est fixée dans l’espace et n’a aucune vitesse, faire 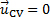. Par conséquent, le flux net de masse par le biais de ce CV est égale à zéro et simplifie à l’équation (1) :

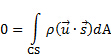(2)

Compte tenu de la configuration dans la Figure 1 a, masse se jette dans le CV à travers port 1 et laisse le CV via le port 2. Par conséquent, la surface intégrale du côté droit de l’équation (2) peut être divisée en deux intégrales indépendants, un pour chaque port. Le signe du produit scalaire est positif en port 2 et négatif dans le port 1 parce que le flux se dirige vers le CV car l’écoulement va éloigner le CV. Sans supposer que la vitesse est distribuée de façon homogène dans un port, laissez-nous faire 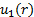et 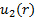les profils de vitesse respective en tenant compte du fait que les deux sont ce qui reste après avoir pris le produit scalaire. Autrement dit, l’amplitude de la composante de vitesse parallèle au vecteur zone, . Enfin, les variations de pression le long de la contraction ne sont pas assez marquées pour induire des changements observables en densité. Désormais, nous pouvons considérer la densité constante. Dans ces conditions, l’équation (2) simplifierait pour :

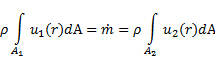(3)

Notez que, étant donné que la masse est conservée, la masse flux, , est le même à travers les deux ports. Compte tenu de la structure de ces relations, chaque partie intégrante dans l’équation (3) exprime le débit volumétrique,, par le biais de son port correspondant et ceci aide de fait pour définir la vitesse moyenne,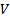, pour un port donné :

(4)

Dans des conditions non visqueux, la vitesse au port 2 pourrait être exprimée en termes de conditions à l’extérieur de l’apport en utilisant l’équation de Bernoulli le long de la centrale (voir Figure 1 a pour référence) :

(5)

Ici, l’effet de hauteur s’évanouit sur la centrale simplifiée parce qu’elle est horizontale et est négligeable chez les autres des lignes de courant, parce que le fluide est l’air qui a une très petite pondération spécifique. En outre, le point initial sur la centrale simplifiée est suffisamment loin de l’entrée que sa vitesse est nulle. Étant donné que l’équation (5) est pour le cas non visqueux idéalisé, cette valeur de la vitesse va être tout partout le même port 2. En réalité, la couche limite la croissance affecte le profil des vitesses et, ce qui la rend non homogènes. Pour tenir compte de cet effet, l’estimation idéale est comparée avec des mesures expérimentales via le « Coefficient de décharge ». Ce coefficient est défini comme le rapport entre la vitesse moyenne mesurée et la vitesse non visqueux pour une section donnée de l’écoulement :

(6)

Le coefficient de débit, , dépend de la géométrie et le nombre de Reynolds. Une fois déterminés, pourrait servir en conjonction avec les équations (4) et (5) pour déterminer le débit à travers port 2 basé sur sa transversale et une facile-à-mesure pression différentielle :

(7)

En posant les équations (4), (5) et (6) ensemble et compte tenu de ce port 2 est circulaire, on obtient la relation suivante pour :

(8)

Il est clair que la connaissance du profil de vitesse est nécessaire pour obtenir le coefficient de débit de l’équation (8). Pour ce faire, nous utiliserons la vélocimétrie par Pitot - statiques sondes. Comme illustré à la Figure 1 b, le tube de Pitot apporte le flux à un arrêt de détection de la pression totale,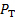, qui est l’addition des pressions statiques et dynamiques à un moment donné. En revanche, la sonde statique au mur détecte la pression statique seule. L’équation de Bernoulli appliquée à une position radiale donnée, la pression totale est constante de juste de Bernoulli. Au port 2, ce principe peut être exprimé par la relation suivante en position radiale arbitraire :

(9)

Ici, nous négligeons l’effet de la position verticale, car notre passage de flux est horizontale. En résumé, on obtient la relation suivante pour la grandeur de la vitesse à une position donnée «r» dans la tuyauterie :

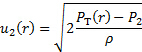(10)

La différence de pression est mesuré directement par la pression transducteur représenté dans la Figure 1 b, et le profil des vitesses est obtenu en parcourant le long de la coordonnée radiale du tube, le tube de Pitot. Notez que ces mesures de vitesse sont effectués à des postes discrets, par conséquent, ces points de données devraient être utilisés pour résoudre l’intégrale dans l’équation (8) numériquement en utilisant la forme trapézoïdale ou règle de Simpson [1]. Une fois la valeur de cette intégrale est obtenue, il doit être branché dans l’équation (8) ainsi que la valeur mesurée de , la densité et le rayon de la gaine, pour obtenir la valeur de pour cette condition d’écoulement particulier. À la répétition de cette expérience pour des conditions d’écoulement différents, nous obtenons un diagramme de dispersion qui pourrait servir à déterminer une relation entre et . Cette relation peut ensuite être remplacée dans l’équation (7) pour déterminer le débit,, en fonction du seul .

1. réglage de l’installation

1. Assurez-vous qu’il n’y a pas de débit dans l’installation.
2. Vérifiez que le système d’acquisition de données suit le schéma de la Figure 1 b.
3. Connectez le port positif du transducteur de pression #1 (pour référence, voir Figure 1 b ) sur le tube de Pitot traversant ().
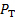4. Connectez le port négatif de ce même capteur de pression de la sonde statique du passage d’admission (). Par conséquent, la lecture de ce transducteur de pression sera directement ().
5. Enregistrer le facteur de conversion de ce transducteur de Volts en Pascals (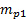). Entrez cette valeur dans le tableau 1.
6. Connectez le port positif du transducteur de pression #2 (pour référence, voir Figure 1 b ) à la sonde statique du passage d’admission () à l’aide d’un tee.
7. Quitter le port négatif du transducteur de pression #2 ouvert à l’atmosphère (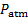). Par conséquent, la lecture de ce capteur sera directement ().
8. Enregistrer le facteur de conversion de ce transducteur de Volts en Pascals (). Entrez cette valeur dans le tableau 1.
9. Définir le système d’acquisition de données de l’échantillon à une fréquence de 100 Hz pour un total de 500 échantillons (c'est-à-dire 5 s des données).
10. Assurez-vous que le canal 1 dans le système d’acquisition de données correspond au capteur de pression #1 ().
11. Entrez le facteur de conversion 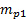dans le système d’acquisition de données pour s’assurer que la mesure de la pression () est directement converti en Pascal.
12. Régler la sonde Pitot à la fin de sa course, où il touche la paroi de la canalisation. Étant donné que la sonde est de 2 mm de diamètre, le premier point de vitesse est à une coordonnée radiale 1 mm du mur. Autrement dit, à une position radiale de mm (ici, mm).

Figure 2 . Paramètre expérimental. (A) : flux de passage à l’étude. (B) : Manuel de système pour le tube de Pitot. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Le tableau 1. Paramètres de base pour l’étude expérimentale. Ameter par valeur

Paramètre	Valeur
Rayon de passage de flux (Ro)	82,25 mm
Constante de calibration transducteur #1 (m_p1)	136.015944 Pa/V
Constante de calibration transducteur #2 (m_p2)	141.241584 N/V
Pression atmosphérique locale	100,474.15 Pa
Température locale	297.15 K
P_atm-P_2	311.01 Pa

2. les mesures

1. Allumez la facilité de circulation.
2. Enregistrer la lecture du transducteur de pression #2 en Volts depuis le multimètre numérique.
3. Entrez cette valeur dans le tableau 1 comme et convertir la lecture d’une tension en Pascals, en utilisant le facteur .
4. Utilisez le système d’acquisition de données pour enregistrer la lecture du ().
5. Entrez la valeur de dans le tableau 2.
6. Utilisez le bouton de déplacement pour changer la position radiale du tube Pitot selon la valeur suggérée dans le tableau 2.
7. Répétez les étapes 2.4 et 2.6 jusqu'à ce que le tableau 2 est complètement rempli.
8. Changer le débit en faisant varier le débit du système.
9. Répétez les étapes 2,4 à 2,8 pour au moins dix différents débits.
10. Désactiver l’installation des flux.

Figure 5 . Paramètre expérimental. Perforé de plaques afin de limiter le débit à la sortie du système flux. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Le tableau 2. Résultats représentatifs. Mesures de la vitesse. r (mm) P_T - P₂ (Pa) u (r) (m/s

r (mm)	P T -P 2 (Pa)	u (r) (m/s)
2.25	300.35	22.34
12.25	302,84	22,43
22.25	305,82	22.54
32.25	302,34	22.41
42,25	294.88	22.13
52,25	295.37	22.15
62,25	292.88	22.06
68,25	293.63	22.09
72.25	294.13	22.10
75,25	299,60	22.31
77.25	293.13	22.07
79,25	284.67	21,75
80.25	256.31	20.63
81,25	198,33	18 h 15

3. analyse.

1. Déterminer le profil des vitesses en utilisant les valeurs d’écart de pression, P_T - P_2, selon le tableau 2. Entrer les résultats dans le tableau 2.
2. Tracer les valeurs de la pression et la vitesse du tableau 2 en utilisant le rayon,, comme l’abcisse (Figure 3).
3. Calculer l’intégrale dans l’équation (8) selon les valeurs de vitesse et le rayon du tableau 2.
4. Calculer le coefficient de débit pour chaque débit utilisant l’équation (8).
5. Tracer le coefficient de décharge à l’aide 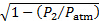comme l’abcisse.
6. Fit une fonction pour le coefficient de débit, une loi de puissance est un bon choix.

Figure 3 . Résultats représentatifs. (A) : exemple de mesure de pression statique le long de la coordonnée radiale du passage du flux. (B) : distribution de vitesse déterminée à partir des mesures de pression statique. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.

Pour une donnée de la restriction du débit à l’évacuation du ventilateur, la Figure 3 a montre les mesures de pression dynamique () à différents endroits radiales à l’intérieur de la conduite après avoir traversé avec le tube de Pitot. Ces valeurs ont été utilisées pour déterminer la vitesse locale dans ces endroits radiales, et les résultats sont illustrés dans la Figure 3 b. Après avoir utilisé la règle du trapèze sur ces données pour résoudre l’équation (4) pour la vitesse moyenne, nous avons obtenu une valeur de m/s. D’autre part, la valeur de du tableau 1 a été utilisé pour déterminer la vitesse idéale de l’équation (5) : m/s. par conséquent, le coefficient de débit pour cette condition d’écoulement est : 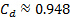. Cette valeur est indiquée dans la Figure 4 comme un triangle rouge.

Après avoir répété cette expérience vingt-neuf fois plus, nous avons obtenu le diagramme illustré à la Figure 4. Ces données peuvent être bien représentées par une loi de puissance de :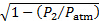

(11)

La raison de ce choix de l’argument est de s’assurer que la constante leader reste sans dimension, et c’est pourquoi cette corrélation serait encore valable quel que soit le système d’unités utilisé pour la pression. Cette fonction peut être substituée dans l’équation (7) pour obtenir le débit en fonction de la :

(12)

Ici, toutes les constantes des équations (7) et (11) ont été regroupées en une seule constante sans dimension :. Par conséquent, équation (12) est valable pour tout système d’unités aussi longtemps que les variables reçoivent constamment des unités correspondantes. Pour plus de commodité, la densité de l’équation (7) a été exprimée en termes de pression atmosphérique et la température absolue en utilisant la Loi des gaz parfaits. Équation (12) est valable pour des conditions atmosphériques différentes puisqu’elle représente des changements dans la pression locale et de la température (T et P_atm). En outre, tant la similitude géométrique est conservée, cette équation serait valide pour passages de différentes tailles comme représenté par le rayon R.

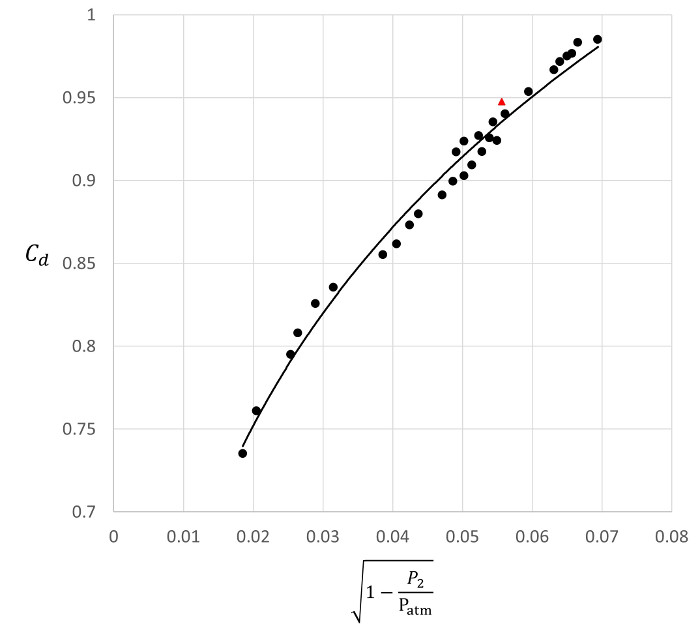
La figure 4. Résultats représentatifs. : Décharger les coefficients déterminés à différents débits. : Coefficient de débit déterminé avec les mesures de la vitesse a démontré ci-après.- : alimentation droit ajustée aux données expérimentales.

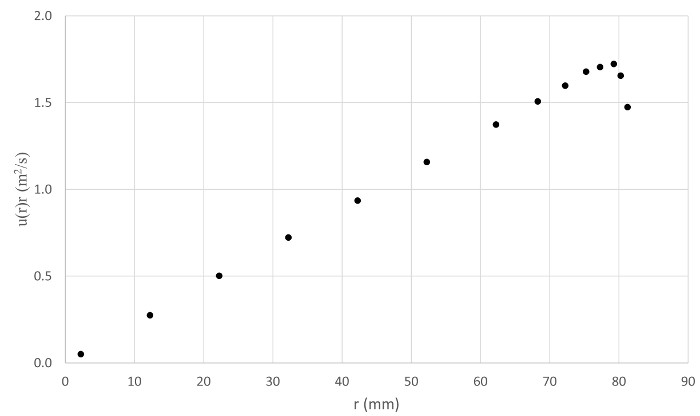
La figure 6. Représentant les résultats. Intrigue du produit entre vitesse et rayon.

Tableau 3. Résultats représentatifs. Coefficient de débit.

√ (1-P2/patm )	Cd
0,019	0.735
0,020	0,761
0.025	0,795
0,026	0.808
0,029	0,826
0,032	0,835
0,039	0,855
0,041	0,862
0,042	0,873
0,044	0,880
0,047	0,891
0,049	0,899
0,049	0,917
0,050	0,924
0,050	0,903
0,051	0,909
0,052	0,927
0,053	0,917
0,054	0.926
0,054	0.935
0,055	0,924
0,056	0,940
0,060	0,953
0,063	0,967
0,064	0.972
0,065	0,975
0,066	0,977
0,067	0.983
0,069	0,985

Nous avons démontré l’application de l’analyse du volume de contrôle de la conservation de la masse pour calibrer un passage de flux comme un débitmètre. À cette fin, nous avons démontré l’utilisation d’un système Pitot-statique pour déterminer le débit à travers le passage de flux grâce à l’intégration sur le profil de vitesse. Ensuite, la notion de coefficient de débit a été constituée pour tenir compte de l’effet de la croissance de la couche limite près des murs du passage du flux. Basé sur un ensemble de mesures de la vitesse pour des débits différents, nous avons développé une régression qui exprime le coefficient de débit en fonction du rapport entre le static pressure au passage de l’écoulement et la pression atmosphérique locale,. Enfin, cette régression a été incorporée dans une équation pour la vitesse d’écoulement dans le passage en fonction de la. Cette équation a été développée à conserve sa validité, au regard des changements de conditions atmosphériques locales, dimensions passage et système d’unités.

Analyse du volume de contrôle pour la conservation de masse offre beaucoup d’alternatives pour calibrer les passages de circulation comme les débitmètres. Par exemple, tôles perforées, buses et tubes de venturi sont utilisés dans les flux confinés pour déterminer le débit basée sur les variations de pression entre deux sections différentes du passage. Et comme pour notre exemple, ces appareils doivent être caractérisés par un coefficient de débit qui corrige les effets de la couche limite.

Débit par l’intermédiaire de canaux ouverts, analyse du volume de contrôle pour la conservation de la masse permet également d’évaluer le débit en comparant la profondeur d’écoulement avant et après des restrictions de débit telles que les déversoirs, écluses partiellement ouvertes ou réductions de section transversale. La signification fondamentale de ces applications est que des ouvrages hydrauliques pour la distribution de l’eau, contrôle et le traitement sont de très grandes échelles qui empêcheraient l’utilisation d’autres dispositifs d’écoulement.