Conservación de masa y mediciones de tasa de flujo
Visión general
Fuente: Ricardo Mejía-Alvarez y Hussam Hikmat Jabbar, Departamento de ingeniería mecánica, Universidad Estatal de Michigan, East Lansing, MI
El propósito de este experimento es demostrar la calibración de un pasaje de flujo como un medidor de caudal utilizando una formulación de volumen (CV) de control [1, 2]. El análisis del CV se centra en el efecto macroscópico de flujo en sistemas de ingeniería, en lugar de la descripción detallada que puede lograrse con un detallado análisis diferencial. Estas dos técnicas deben considerarse como enfoques complementarios, como el análisis de CV dará al ingeniero forma inicial en que ruta a seguir cuando se diseña un sistema de flujo. En términos generales, un análisis de CV le dará una idea del intercambio de masas dominante el ingeniero en un sistema e idealmente debe ser el paso inicial antes de perseguir cualquier diseño detallado o análisis a través de la formulación diferencial.
El principio principal detrás de la formulación de la CV para la conservación de la masa es sustituir los detalles de un sistema de flujo por un volumen simplificado incluido en lo que se conoce como la superficie de control (CS). Este concepto es imaginario y puede ser definido libremente para simplificar hábilmente el análisis. Por ejemplo, el CS debe 'cortar' puertos de entrada y salida en una dirección perpendicular a la velocidad dominante. Entonces, el análisis consistiría en encontrar el equilibrio entre el flujo de masa neto a través de la CS y la tasa de cambio de masa dentro de la CV. Esta técnica se demostrará con la calibración de una contracción suave como un medidor de caudal.
Principios
Un volumen de control (CV) es definido por una superficie cerrada imaginaria, como la superficie de control (CS), definida arbitrariamente para estudiar el balance de masa en un sistema. Figura 1A se muestra un ejemplo de un volumen de control que contiene una región de flujo va a través de un pasaje de flujo. Los detalles del flujo en el pasaje son irrelevantes ya que estamos sólo interesados en la obtención de medidas de la afluencia masiva, de la salida y su tasa de cambio en el paso del flujo. Todos estos efectos se pueden resumir en la ecuación de conservación de la masa en forma integral [1, 2]:
 (1)
(1)
El primer término del lado derecho de la ecuación (1) representa la tasa de cambio de masa dentro del volumen de control, mientras que el segundo término representa el flujo neto de masa a través de la superficie de control. La diferencia del vector 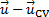 es la velocidad relativa entre el CV y el flujo y el vector de
es la velocidad relativa entre el CV y el flujo y el vector de  es la unidad hacia fuera normal que el diferencial de área. El producto escalar entre la velocidad relativa y
es la unidad hacia fuera normal que el diferencial de área. El producto escalar entre la velocidad relativa y  representa el componente de velocidad que cruza el CS y en lo sucesivo contribuye al intercambio de masa. El símbolo de este producto de punto es negativa donde se dirige el flujo de masa en el CV y positivo donde se dirige lejos de la CV.
representa el componente de velocidad que cruza el CS y en lo sucesivo contribuye al intercambio de masa. El símbolo de este producto de punto es negativa donde se dirige el flujo de masa en el CV y positivo donde se dirige lejos de la CV.

Figura 1. SChemática de configuración básica. (A) admisión liso para un ventilador centrífugo. El volumen de control se define como el perfil del paso. Excluyen a las paredes sólidas del volumen de control, pero sus condiciones de contorno se mantienen en la superficie de control (es decir, sin penetración y no deslizar). Puerto 1 se define como el lado de la entrada del pasaje, mientras que el puerto 2 se define como el plano transversal que coincide con la punta del tubo Pitot. Flujo va de izquierda a derecha. (B) sistema tubo de Pitot-estática y schematic de sistema de adquisición de datos. Haga clic aquí para ver una versión más grande de esta figura.
Para la presente manifestación, contamos con las configuraciones que se muestra en la figura 1A, donde un currículum fijo sigue el contorno de la suave contracción en el consumo de un ventilador centrífugo. El flujo a través de esta CV es constante, por lo tanto la tasa de cambio de masa dentro del volumen de control es cero. Por lo tanto, el primer término del lado derecho de la ecuación (1) desaparece. Además, el CV se une a la contracción, que se fija en el espacio y no velocidad, haciendo 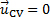 . Por lo tanto, el flujo neto de masa a través de esta CV es cero y la ecuación (1) se simplifica a:
. Por lo tanto, el flujo neto de masa a través de esta CV es cero y la ecuación (1) se simplifica a:
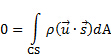 (2)
(2)
Teniendo en cuenta la configuración en la figura 1A, masa fluye en el CV a través del puerto 1 y deja el CV a través del puerto 2. En consecuencia, la superficie integral en el lado derecho de la ecuación (2) se puede dividir en dos integrales independientes, uno para cada puerto. El signo del producto de punto es negativa en Puerto 1 porque el flujo va hacia el CV y positivo en el puerto 2 porque el flujo va de la CV. Sin asumir que la velocidad se distribuye homogéneamente en cualquiera de los puertos, hagamos 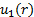 y
y 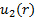 los perfiles de velocidad correspondiente teniendo en cuenta que ambos son lo que queda después de tomar el producto de punto. Es decir, la magnitud de la componente de velocidad paralela al vector área,
los perfiles de velocidad correspondiente teniendo en cuenta que ambos son lo que queda después de tomar el producto de punto. Es decir, la magnitud de la componente de velocidad paralela al vector área,  . Finalmente, cambios de presión a lo largo de la contracción no están lo suficientemente significativos como para inducir a cambios observables en la densidad. En adelante, podemos considerar la densidad como constante. En estas circunstancias, ecuación (2) se simplifica:
. Finalmente, cambios de presión a lo largo de la contracción no están lo suficientemente significativos como para inducir a cambios observables en la densidad. En adelante, podemos considerar la densidad como constante. En estas circunstancias, ecuación (2) se simplifica:
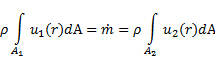 (3)
(3)
Tenga en cuenta que, puesto que la masa se conserva, la masa fundente,  , es la misma a través de ambos puertos. Dada la estructura de estas relaciones, cada integral en la ecuación (3) expresa la velocidad de flujo volumétrico,
, es la misma a través de ambos puertos. Dada la estructura de estas relaciones, cada integral en la ecuación (3) expresa la velocidad de flujo volumétrico, , a través de su puerto correspondiente y este hecho ayuda a definir la velocidad media,
, a través de su puerto correspondiente y este hecho ayuda a definir la velocidad media,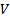 , para un puerto determinado:
, para un puerto determinado:
 (4)
(4)
Condiciones no viscoso, la velocidad en el puerto 2 podría ser expresada en términos de las condiciones fuera de la entrada usando la ecuación de Bernoulli a lo largo de la central aerodinámico (véase figura 1A para la referencia):
 (5)
(5)
Aquí, el efecto de la altura desaparece en el centro aerodinámico porque es horizontal y es insignificante en las otras líneas, debido a que el fluido es aire, que tiene un peso específico muy pequeño. También, el punto inicial en el centro aerodinámico está suficientemente lejos de la entrada que su velocidad es cero. Dado que la ecuación (5) es para el caso no viscoso idealizado, este valor de velocidad va ser el mismo todo a través puerto 2. En realidad, crecimiento de la capa límite afecta el perfil de velocidad y es no homogénea. Para tener en cuenta este efecto, la estimación ideal es comparada con mediciones experimentales mediante el "coeficiente de descarga". Este coeficiente se define como el cociente entre la velocidad promedio medida y la velocidad no viscoso para una sección dada del flujo:
 (6)
(6)
El coeficiente de descarga,  , depende de la geometría y el número de Reynolds. Una vez determinado,
, depende de la geometría y el número de Reynolds. Una vez determinado,  podría ser utilizado en conjunción con las ecuaciones (4) y (5) para determinar la tasa de flujo a través del puerto 2 basado en su área de sección transversal y un diferencial de presión de fácil medida:
podría ser utilizado en conjunción con las ecuaciones (4) y (5) para determinar la tasa de flujo a través del puerto 2 basado en su área de sección transversal y un diferencial de presión de fácil medida:
 (7)
(7)
Al poner las ecuaciones (4), (5) y (6) juntos y teniendo en cuenta que el puerto 2 son circular, obtenemos la siguiente relación para  :
:
 (8)
(8)
Es evidente de la ecuación (8) que el conocimiento del perfil de velocidad es necesario para obtener el coeficiente de descarga. Para ello, haremos uso de velocimetría por Pitot - estática sondas. Como se muestra en la figura 1B, el tubo de Pitot trae el flujo a una parada de detección de la presión total,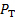 , que es la suma de las presiones estáticas y dinámicas en un momento dado. Por otra parte, la sonda estática en la pared detecta la presión estática solo. De la ecuación de Bernoulli aplicado a una determinada posición radial, la presión total es constante sólo de la de Bernoulli. En el puerto 2, este principio puede expresarse por la siguiente relación en una posición radial arbitraria:
, que es la suma de las presiones estáticas y dinámicas en un momento dado. Por otra parte, la sonda estática en la pared detecta la presión estática solo. De la ecuación de Bernoulli aplicado a una determinada posición radial, la presión total es constante sólo de la de Bernoulli. En el puerto 2, este principio puede expresarse por la siguiente relación en una posición radial arbitraria:
 (9)
(9)
Aquí, estamos descuidando el efecto de la posición vertical debido a que el paso del flujo es horizontal. En Resumen, se obtiene la siguiente relación de la magnitud de la velocidad en una determinada posición 'r' dentro de la tubería:
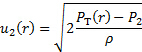 (10)
(10)
La diferencia de presión  se mide directamente por la presión del transductor se muestra en la figura 1B, y el perfil de velocidad se obtiene recorriendo el tubo de Pitot a lo largo de la coordenada radial de la tubería. Tenga en cuenta que las mediciones de velocidad se llevan a cabo en posiciones discretas, por lo tanto, estos puntos de datos se deben utilizar para resolver la integral en la ecuación (8) numéricamente utilizando la trapezoidal o regla de Simpson [1]. Una vez obtenido el valor de esta integral, debe estar conectado en la ecuación (8) junto con el valor medido de
se mide directamente por la presión del transductor se muestra en la figura 1B, y el perfil de velocidad se obtiene recorriendo el tubo de Pitot a lo largo de la coordenada radial de la tubería. Tenga en cuenta que las mediciones de velocidad se llevan a cabo en posiciones discretas, por lo tanto, estos puntos de datos se deben utilizar para resolver la integral en la ecuación (8) numéricamente utilizando la trapezoidal o regla de Simpson [1]. Una vez obtenido el valor de esta integral, debe estar conectado en la ecuación (8) junto con el valor medido de  , la densidad y el radio del conducto, para obtener el valor de
, la densidad y el radio del conducto, para obtener el valor de  para esa condición de flujo particular. Al repetir este experimento para condiciones de flujo distintos, obtendremos un diagrama de dispersión que podría utilizarse para determinar una relación entre
para esa condición de flujo particular. Al repetir este experimento para condiciones de flujo distintos, obtendremos un diagrama de dispersión que podría utilizarse para determinar una relación entre  y
y  . Esta relación entonces puede sustituirse en la ecuación (7) para determinar completamente la velocidad de flujo,
. Esta relación entonces puede sustituirse en la ecuación (7) para determinar completamente la velocidad de flujo, , como una función de sólo
, como una función de sólo  .
.
Procedimiento
1. configuración de la instalación
- Asegúrese de que no hay ningún flujo en la instalación.
- Verificar que el sistema de adquisición de datos sigue el esquema en la figura 1B.
- Conecte el positivo del transductor de presión #1 (ver figura 1B para referencia) en el tubo de Pitot atraviesa (
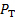 ).
). - Conecte el puerto negativo de este mismo transductor de presión a la sonda estática del pasaje de ingesta (
 ). Por lo tanto, la lectura de este transductor de presión será directamente (
). Por lo tanto, la lectura de este transductor de presión será directamente ( ).
). - Registrar el factor de conversión de este transductor de voltios a pascales (
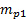 ). Introduzca este valor en la tabla 1.
). Introduzca este valor en la tabla 1. - Conecte el puerto positivo del transductor de presión #2 (ver figura 1B para referencia) a la sonda estática del pasaje de ingesta (
 ) usando una camiseta.
) usando una camiseta. - Salir del puerto negativo del transductor de presión #2 abierto a la atmósfera (
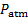 ). Por lo tanto, la lectura de este transductor será directamente (
). Por lo tanto, la lectura de este transductor será directamente ( ).
). - Registrar el factor de conversión de este transductor de voltios a pascales (
 ). Introduzca este valor en la tabla 1.
). Introduzca este valor en la tabla 1. - Establecer el sistema de adquisición de datos a la muestra a una frecuencia de 100 Hz para un total de 500 muestras (es decir, 5s de datos).
- Asegúrese de que ese canal 1 en el sistema de adquisición de datos corresponde a transductor de presión #1 (
 ).
). - Introduzca el factor de conversión
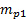 en el sistema de adquisición de datos para asegurarse de que la medición de la presión (
en el sistema de adquisición de datos para asegurarse de que la medición de la presión ( ) se convierte directamente en Pascal.
) se convierte directamente en Pascal. - Fijar la sonda Pitot al final de su recorrido, donde toca la pared de la tubería. Desde la punta de prueba es de 2 mm de diámetro, es el primer punto de velocidad en una coordenada radial 1 mm de la pared. Es decir, en una posición radial de
 mm (aquí,
mm (aquí, mm).
mm).

Figura 2 . Ajuste experimental. (A): flujo de pasaje bajo estudio. (B): manual de atravesar el sistema para el tubo de Pitot. Haga clic aquí para ver una versión más grande de esta figura.
Tabla 1. Parámetros básicos para el estudio experimental. Par ámetro valor
| Parámetro | Valor |
| Radio de paso de flujo (Ro) | 82,25 mm |
| Constante de calibración del transductor #1 (m_p1) | 136.015944 Pa/V |
| Constante de calibración del transductor #2 (m_p2) | 141.241584 N/V |
| Presión atmosférica local | 100,474.15 Pa |
| Temperatura local | 297.15 K |
| P_atm-P_2 | 311.01 Pa |
2. las medidas
- Encienda la facilidad de flujo.
- Grabar la lectura del transductor de presión #2 en voltios en el multimetro digital.
- Introduzca este valor en la tabla 1 como
 y convertir la lectura de voltios a Pascal con el factor de
y convertir la lectura de voltios a Pascal con el factor de  .
. - Utilizar el sistema de adquisición de datos para registrar la lectura de (
 ).
). - Introduzca el valor de
 en la tabla 2.
en la tabla 2. - Use el botón móvil para cambiar la posición radial del tubo de Pitot según el valor sugerido en la tabla 2.
- Repita los pasos del 2.4 y 2.6 hasta tabla 2 está totalmente poblada.
- Cambiar el caudal mediante la variación de la descarga del sistema.
- Repita los pasos del 2.4 a 2.8 para por lo menos diez diferentes caudales.
- Apague la facilidad de flujo.

Figura 5 . Ajuste experimental. Perforado de placas para restringir el flujo en la descarga del sistema de flujo. Haga clic aquí para ver una versión más grande de esta figura.
Tabla 2. Resultados representativos. Mediciones de velocidad. r (mm) PT - P2 (Pa) u (r) (m/s
| r (mm) | P T -P 2 (Pa) | u (r) (m/s) |
| 2.25 | 300.35 | 22.34 |
| 12.25 | 302.84 | 22.43 |
| 22.25 | 305.82 | 22.54 |
| 32.25 | 302.34 | 22,41 |
| 42.25 | 294.88 | 22.13 |
| 52.25 | 295.37 | 22.15 |
| 62.25 | 292.88 | 22.06 |
| 68.25 | 293.63 | 22.09 |
| 72.25 | 294.13 | 22.10 |
| 75.25 | 299.60 | 22.31 |
| 77.25 | 293.13 | 22.07 |
| 79.25 | 284.67 | 21,75 |
| 80.25 | 256.31 | 20,63 |
| 81.25 | 198.33 | 18.15 |
3. los datos análisis.
- Determinar el perfil de velocidad utilizando los valores de diferencia de presión, PT - P2, tabla 2. Introducir los resultados en la tabla 2.
- Trama de valores de la presión y la velocidad de cuadro 2 usando el radio,
 , como las abscisas (figura 3).
, como las abscisas (figura 3). - Calcular la integral en la ecuación (8) basada en los valores de velocidad y radio de tabla 2.
- Calcular el coeficiente de descarga para cada caudal con la ecuación (8).
- Parcela el coeficiente de descarga usando
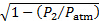 como las abscisas.
como las abscisas. - Ajuste de una función para el coeficiente de descarga, una ley de potencia es una buena opción.

Figura 3 . Resultados representativos. (A): ejemplo de medición de la presión estática a lo largo de la coordenada radial del paso del flujo. (B): distribución de velocidad determinado a partir de las mediciones de presión estática. Haga clic aquí para ver una versión más grande de esta figura.
Resultados
Para una determinada restricción del flujo en la descarga del ventilador, Figura 3A muestra las medidas de presión dinámica ( ) en diferentes lugares radiales dentro de la tubería después de atravesar con el tubo de Pitot. Estos valores fueron utilizados para determinar la velocidad local en esos lugares radiales, y los resultados se muestran en la figura 3B. Después de usar la regla trapezoidal en estos datos para resolver la ecuación (4) para la velocidad media, obtuvimos un valor de
) en diferentes lugares radiales dentro de la tubería después de atravesar con el tubo de Pitot. Estos valores fueron utilizados para determinar la velocidad local en esos lugares radiales, y los resultados se muestran en la figura 3B. Después de usar la regla trapezoidal en estos datos para resolver la ecuación (4) para la velocidad media, obtuvimos un valor de m/s. Por otra parte, el valor de
m/s. Por otra parte, el valor de  de la tabla 1 se utilizó para determinar la velocidad ideal de la ecuación (5):
de la tabla 1 se utilizó para determinar la velocidad ideal de la ecuación (5):  m/s. por lo tanto, el coeficiente de descarga para esta condición de flujo es:
m/s. por lo tanto, el coeficiente de descarga para esta condición de flujo es: 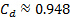 . Este valor se muestra en la figura 4 como un triángulo rojo.
. Este valor se muestra en la figura 4 como un triángulo rojo.
Después de repetir este experimento veintinueve veces más, se obtuvo el diagrama de dispersión que se muestra en la figura 4. Esta información puede ser bien representada por una ley de potencia de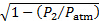 :
:
 (11)
(11)
La razón de esta elección del argumento es que la constante principal permanece sin dimensiones, y por lo tanto, esta correlación seguiría siendo válida independientemente del sistema de unidades utilizado para la presión. Esta función puede sustituirse en la ecuación (7) para obtener el caudal en función de la :
:
 (12)
(12)
Aquí, todas las constantes de las ecuaciones (7) y (11) fueron mezclados en una sola constante adimensional: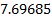 . En consecuencia, la ecuación (12) es válido para cualquier sistema de unidades como las variables siempre se asignan a las unidades correspondientes. Para mayor comodidad, la densidad de la ecuación (7) se expresó en términos de presión atmosférica y temperatura absoluta utilizando la ley de gas ideal. Ecuación (12) es válida para diferentes condiciones atmosféricas como representa cambios en el local de la presión y temperatura (T y Patm). También, como se conserva la semejanza geométrica, esta ecuación sería válida para pasajes de diferentes tamaños como por el radio R.
. En consecuencia, la ecuación (12) es válido para cualquier sistema de unidades como las variables siempre se asignan a las unidades correspondientes. Para mayor comodidad, la densidad de la ecuación (7) se expresó en términos de presión atmosférica y temperatura absoluta utilizando la ley de gas ideal. Ecuación (12) es válida para diferentes condiciones atmosféricas como representa cambios en el local de la presión y temperatura (T y Patm). También, como se conserva la semejanza geométrica, esta ecuación sería válida para pasajes de diferentes tamaños como por el radio R.
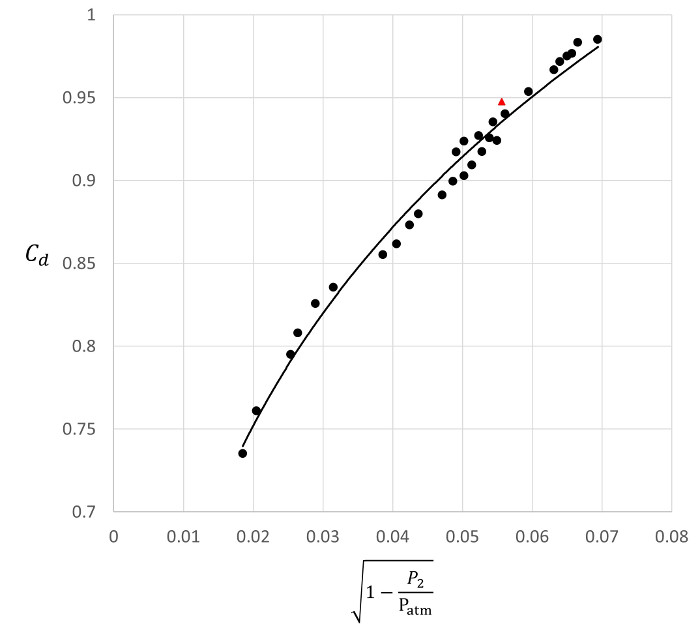
Figura 4. Resultados representativos.  : Coeficientes determinados en diferentes caudales de descarga.
: Coeficientes determinados en diferentes caudales de descarga.  : Coeficiente de descarga con las mediciones de velocidad demostrada aquí.-: derecho a los datos experimentales de la energía.
: Coeficiente de descarga con las mediciones de velocidad demostrada aquí.-: derecho a los datos experimentales de la energía.
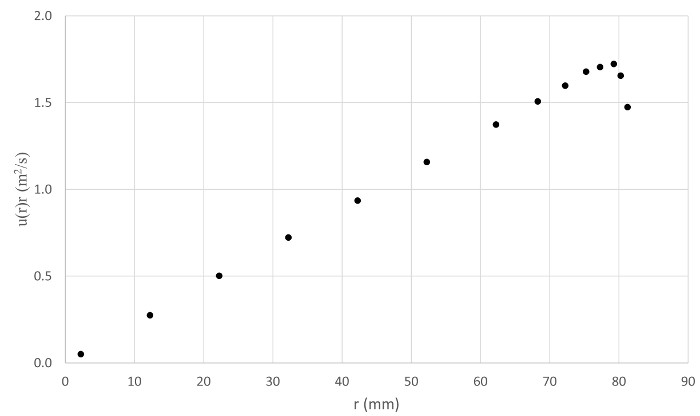
Figura 6. Resultados de la representante. Diagrama del producto entre la velocidad y radio.
Tabla 3. Resultados representativos. Coeficiente de descarga.
| √ (1-P2/Patm ) | Cd |
| 0.019 | 0.735 |
| 0.020 | 0.761 |
| 0.025 | 0.795 |
| 0.026 | 0.808 |
| 0.029 | 0.826 |
| 0.032 | 0.835 |
| 0.039 | 0.855 |
| 0,041 | 0.862 |
| 0,042 | 0.873 |
| 0.044 | 0.880 |
| 0.047 | 0.891 |
| 0.049 | 0.899 |
| 0.049 | 0.917 |
| 0.050 | 0.924 |
| 0.050 | 0.903 |
| 0,051 | 0.909 |
| 0.052 | 0,927 |
| 0.053 | 0.917 |
| 0.054 | 0,926 |
| 0.054 | 0,935 |
| 0.055 | 0.924 |
| 0.056 | 0,940 |
| 0.060 | 0.953 |
| 0.063 | 0.967 |
| 0,064 | 0.972 |
| 0,065 | 0.975 |
| 0.066 | 0.977 |
| 0.067 | 0.983 |
| 0.069 | 0.985 |
Aplicación y resumen
Hemos demostrado la aplicación del análisis del volumen control de conservación de masa para calibrar un pasaje de flujo como un medidor de flujo. Para ello, hemos demostrado el uso de un sistema Pitot-estático para determinar la tasa de flujo a través del paso del flujo mediante la integración sobre el perfil de velocidad. Luego, se incorporó el concepto de coeficiente de descarga para tener en cuenta el efecto del crecimiento de la capa límite cerca de las murallas del paso del flujo. Basado en un conjunto de mediciones de velocidad para diferentes caudales, desarrollamos una regresión que expresa el coeficiente de descarga en función de la relación entre la static pressure en el pasaje de flujo y la presión atmosférica local, . Por último, esta regresión se incorporó una ecuación para el flujo a través del paso en función de la
. Por último, esta regresión se incorporó una ecuación para el flujo a través del paso en función de la . Esta ecuación fue desarrollada a mantiene su validez ante cambios en las condiciones atmosféricas locales, el tamaño de paso y sistema de la unidad.
. Esta ecuación fue desarrollada a mantiene su validez ante cambios en las condiciones atmosféricas locales, el tamaño de paso y sistema de la unidad.
Análisis del volumen de control para la conservación de la masa ofrecen muchas alternativas para calibrar pasajes de flujo como medidores de flujo. Por ejemplo, placas perforadas, toberas y tubos venturi se utilizan en flujos confinados para determinar caudal basado en cambios de presión entre dos secciones diferentes del paso. Y similar a nuestro ejemplo, estos dispositivos necesitan ser caracterizado con un coeficiente de descarga que corrige para los efectos de capa límite.
En el flujo a través de canales abiertos, análisis de volumen de control para la conservación de la masa también pueden utilizarse para evaluar caudal comparando la profundidad del flujo antes y después de las restricciones de flujo tales como aliviaderos, puertas parcialmente abiertas o reducciones de sección. La principal importancia de estas aplicaciones es que son estructuras hidráulicas de distribución de agua, control y tratamiento de escalas muy grandes que impidan el uso de otros dispositivos de flujo.
Referencias
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
- Chapra, S.C. and R.P. Canale. Numerical methods for engineers. Vol. 2. New York: McGraw-Hill, 1998.
- Buckingham, E. Note on contraction coefficients of jets of gas. Journal of Research, 6:765-775, 1931.
- Lienhard V, J.H. and J.H. Lienhard IV. Velocity coefficients for free jets from sharp-edged orifices. ASME Journal of Fluids Engineering, 106:13-17, 1984.
Tags
Saltar a...
Vídeos de esta colección:

Now Playing
Conservación de masa y mediciones de tasa de flujo
Mechanical Engineering
22.6K Vistas

Flotabilidad y arrastre en cuerpos sumergidos
Mechanical Engineering
29.9K Vistas

Estabilidad de los buques flotantes
Mechanical Engineering
22.4K Vistas

Propulsión y empuje
Mechanical Engineering
21.6K Vistas

Redes de tuberías y pérdidas de presión
Mechanical Engineering
58.0K Vistas

Enfriamiento y ebullición
Mechanical Engineering
7.7K Vistas

Saltos hidráulicos
Mechanical Engineering
40.9K Vistas

Análisis del intercambiador de calor
Mechanical Engineering
28.0K Vistas

Introducción a la refrigeración
Mechanical Engineering
24.6K Vistas

Anemometría de hilo caliente
Mechanical Engineering
15.5K Vistas

Medición de flujos turbulentos
Mechanical Engineering
13.5K Vistas

Visualización de flujo más allá de un cuerpo no fuselado
Mechanical Engineering
11.8K Vistas

Jet que inciden sobre una placa inclinada
Mechanical Engineering
10.7K Vistas

Enfoque de conservación de la energía para el análisis de sistemas
Mechanical Engineering
7.4K Vistas

Determinación de las fuerzas de impacto en una placa plana con el método del control del volumen
Mechanical Engineering
26.0K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados