质量守恒和流速测量
Overview
资料来源: 里卡多梅希亚-阿尔瓦雷斯和 Hussam Hikmat, 密歇根州立大学机械工程系, 东兰辛, MI
本实验的目的是演示使用控制容积 (CV) 配方 [1, 2] 的流量通道作为流量计的校准。CV 分析的重点是流对工程系统的宏观影响, 而不是详细的微分分析可以实现的详细描述。这两种技术应该被认为是互补的方法, 因为 CV 分析将使工程师在设计一个流程系统时, 能在哪条路径上进行初始化。从广义上讲, CV 分析将给工程师一个系统中主导的质量交换的概念, 最好是在通过差分公式进行详细设计或分析之前采取的最初步骤。
质量守恒的 CV 公式的主要原理是用被称为控制面 (CS) 的简化体积来替换流系统的细节。这个概念是虚构的, 可以自由定义, 巧妙地简化分析。例如, CS 应 "切割" 入口和出口端口, 其方向与主速度垂直。然后, 通过 CS 的净质量通量与 CV 内质量变化率之间的平衡, 进行分析。这项技术将被证明与平滑收缩作为流量计的校准。
Principles
控制容积 (CV) 由假想的闭合表面定义, 被称为控制面 (CS), 任意定义以研究系统中的质量平衡。图1A 显示了一个控制卷的例子, 其中包含一个流经流通道的流区域。在通道中的流量的细节是不相干的, 因为我们只是有兴趣获得的质量流入, 流出, 其变化率的流量通道内的措施。所有这些作用可以总结在等式为质量守恒在缺一不可的形式 [1, 2]:
 (1)
(1)
第一个术语在等式的右手边 (1) 代表质量变动率在控制容量之内, 而第二个期限代表净通量通过控制表面。向量差异是 CV 和流之间的相对速度, 向量是该区域差异的向外正常的单位. 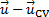
 相对速度和之间的点积表示跨越 CS 的速度分量, 从而有助于进行质量交换.
相对速度和之间的点积表示跨越 CS 的速度分量, 从而有助于进行质量交换.  这个点产品的标志是负的, 当质量通量被引导入 cv 和正面, 它被指挥从 cv。
这个点产品的标志是负的, 当质量通量被引导入 cv 和正面, 它被指挥从 cv。

图1。Sc基本配置的血。(a) 离心风机的平稳进气。控制音量被定义为段落的内部轮廓。实体壁从控制卷中排除, 但其边界条件保存在控制曲面中 (即不穿透和无滑动)。端口1被定义为通道的入口侧, 而端口2定义为与托管管的顶端重合的横截面平面。流从左向右。(B) schemati 静态系统和数据获取系统的 c.请单击此处查看此图的较大版本.
对于目前的演示, 我们有图1A 所示的配置, 其中固定 CV 遵循的轮廓, 作为平稳收缩在进气口离心风扇。通过该 CV 的流量是稳定的, 因此在控制容积内的质量变化率为零。因此, 在等式 (1) 右手边的第一个术语消失了。此外, CV 附加到收缩, 这是固定在空间和没有速度, 使. 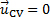 因此, 通过这个 CV 的质量净流量为零, 而等式 (1) 简化为:
因此, 通过这个 CV 的质量净流量为零, 而等式 (1) 简化为:
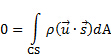 (2)
(2)
考虑到图1A 中的配置, 质量在端口1中流入 cv, 并在端口2中留下 cv。因此, 方程 (2) 右侧的表面积分可以分为两个独立的积分, 一个用于每个端口。在端口1中, 点积的符号为负, 因为流流向 cv, 在端口2中为正值, 因为流量从 cv 中消失。假设速度在任一端口均是均匀分布的, 则让我们使和各自的速度配置文件考虑到两者都是在取点积后留下的东西. 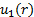
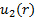 即, 速度分量与区域向量平行的大小,.
即, 速度分量与区域向量平行的大小,.  最后, 沿收缩的压力变化并不显著, 足以诱发密度的可观测变化。从今往后, 我们可以把密度看成常数。在这种情况下, 等式 (2) 将简化为:
最后, 沿收缩的压力变化并不显著, 足以诱发密度的可观测变化。从今往后, 我们可以把密度看成常数。在这种情况下, 等式 (2) 将简化为:
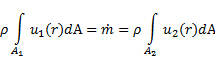 (3)
(3)
请注意, 由于质量是守恒的, 因此质量通量 () 在两个端口上是相同的.  考虑到这些关系的结构, 等式 (3) 中的每个积分都通过其对应的端口表示容积流速, 这一事实有助于定义给定端口的平均速度 ():
考虑到这些关系的结构, 等式 (3) 中的每个积分都通过其对应的端口表示容积流速, 这一事实有助于定义给定端口的平均速度 ():
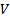
 (4)
(4)
在无粘的条件下, 2 端口的速度可以用伯努利方程沿中心流线的进气条件来表示 (参见图 1A):
 (5)
(5)
在这里, 高度的影响在中央流线上消失了, 因为它是水平的, 在其他流线上是微不足道的, 因为流体是空气, 它有非常小的比重。此外, 中央流线上的初始点离入口很远, 其速度为零。考虑到等式 (5) 是理想化的无粘的情况, 这个速度的值将是相同的整个端口2。在实际中, 边界层的生长影响速度剖面, 使其不均匀。考虑到这一效果, 将理想的估计值与通过 "放电系数" 进行的实验测量进行比较。该系数定义为流的给定截面的测量平均速度和无粘速度之间的比值:
 (6)
(6)
放电系数,, 取决于几何和雷诺数.  一旦确定, 可与公式 (4) 和 (5) 结合使用, 以确定基于其横截面面积和易于测量的压力差的端口2的流速:
一旦确定, 可与公式 (4) 和 (5) 结合使用, 以确定基于其横截面面积和易于测量的压力差的端口2的流速: 
 (7)
(7)
在将等式 (4)、(5) 和 (6) 放在一起时, 并考虑到端口2是循环的, 我们获得以下关系: 
 (8)
(8)
从方程 (8) 可以清楚地看出, 速度剖面的知识是获得放电系数所必需的。为此, 我们将使用测速仪的皮托管静态探头。如图1B 所示, 皮托管管带来的流量, 以停止传感总压力,, 这是增加了静态和动态压力在一个给定的点.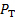 另一方面, 在墙上的静态探头只感觉到静压。从伯努利方程应用于给定的径向位置, 总压强只是伯努利常数。在端口 2, 这一原则可以通过以下关系在任意径向位置表示:
另一方面, 在墙上的静态探头只感觉到静压。从伯努利方程应用于给定的径向位置, 总压强只是伯努利常数。在端口 2, 这一原则可以通过以下关系在任意径向位置表示:
 (9)
(9)
在这里, 我们忽略了垂直位置的影响, 因为我们的流动通道是水平的。总之, 在管道内给定位置 "r" 的速度的大小, 你得到以下关系:
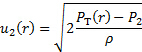 (10)
(10)
压力差由图1B 中所示的压力传感器直接测量, 通过沿管的径向坐标遍历托管管来获得速度剖面.  请注意, 这些速度测量是在离散位置进行的, 因此, 这些数据点应用于解决方程 (8) 中的积分, 使用梯形或辛普森的规则 [1]。一旦得到这个积分的值 , 它应该入到等式 ( 8 ) 连同测量值的 , 密度和管道的半径 , 以获得该特定的流条件的值 .
请注意, 这些速度测量是在离散位置进行的, 因此, 这些数据点应用于解决方程 (8) 中的积分, 使用梯形或辛普森的规则 [1]。一旦得到这个积分的值 , 它应该入到等式 ( 8 ) 连同测量值的 , 密度和管道的半径 , 以获得该特定的流条件的值 . 
 在对不同的流条件重复此实验后, 我们将获得一个散点图, 可用于确定和之间的关系.
在对不同的流条件重复此实验后, 我们将获得一个散点图, 可用于确定和之间的关系. 
 然后, 可以在公式 (7) 中替换此关系, 以完全确定流率作为单独的函数.
然后, 可以在公式 (7) 中替换此关系, 以完全确定流率作为单独的函数.

Procedure
1. 设置设施
- 确保设施中没有流动。
- 验证数据获取系统是否遵循图 1B中的示意图。
- 将压力传感器的正端口连接 #1 (参见图 1B以供参考) 到遍历的托管管 ().
- 将此相同压力传感器的负端口连接到进气通道的静态探头 ().
 因此, 这种压力传感器的读数将直接 ().
因此, 这种压力传感器的读数将直接 ().
- 将此传感器的转换系数从伏特记录到帕斯卡 ().
 在表1中输入此值。
在表1中输入此值。 - 将压力传感器的正端口连接 #2 (参见图 1B以供参考) 到使用 tee 的进气通道 () 的静态探头.

- 离开压力传感器的负端口 #2 向大气开放 ().
 因此, 该传感器的读数将直接 ().
因此, 该传感器的读数将直接 ().
- 将此传感器的转换系数从伏特记录到帕斯卡 ().
 在表1中输入此值。
在表1中输入此值。 - 将数据采集系统设置为采样速率为100赫兹, 共500样本 (即5s 数据)。
- 确保数据采集系统中的通道1对应于压力传感器 #1 ().

- 在数据采集系统中输入转换因子, 以确保压力测量 () 直接转换为帕斯卡.
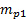

- 在旅行结束时, 把皮托管探针放在它碰到管子壁的地方。由于探头直径为2毫米, 第一个速度点在距墙1毫米的径向坐标处。即, 在 mm (此处为 mm) 的径向位置.



图 2.实验设置。(A): 正在研究的流动通道。(B): 皮托管管的手动遍历系统.请单击此处查看此图的较大版本.
表1。实验研究的基本参数。Par ameter 值
| 参数 | 值 |
| 流通道半径 (Ro) | 82.25 毫米 |
| 传感器 #1 校准常数 (m_p1) | 136.015944 Pa/五 |
| 传感器 #2 校准常数 (m_p2) | 141.241584 N/伏 |
| 局部气压 | 100474.15 Pa |
| 局部温度 | 297.15 K |
| P_atm-P_2 | 311.01 Pa |
2. 测量
- 打开流设备。
- 从数字万用表中记录压力传感器 #2 电压的读数。
- 在表1中输入此值作为, 并使用因子将读数从伏特转换为帕斯卡.


- 使用数据获取系统记录读取 ().

- 在表2中输入的值.

- 根据表2中建议的值, 使用遍历旋钮改变皮托管管的径向位置。
- 重复步骤2.4 和 2.6, 直到表2完全填充为止。
- 通过改变系统的放电速度来更改流量。
- 对至少十不同的流速重复步骤2.4 到2.8。
- 关闭流设备。

图 5.实验设置。穿孔板限制流量在流量系统的放电.请单击此处查看此图的较大版本.
表2。代表性的结果。速度测量。r (mm) pT -P2 (Pa) u (r) (m/秒
| r(mm) | PT-p2(Pa) | u(r) (m/秒) |
| 2.25 | 300.35 | 22.34 |
| 12.25 | 302.84 | 22.43 |
| 22.25 | 305.82 | 22.54 |
| 32.25 | 302.34 | 22.41 |
| 42.25 | 294.88 | 22.13 |
| 52.25 | 295.37 | 22.15 |
| 62.25 | 292.88 | 22.06 |
| 68.25 | 293.63 | 22.09 |
| 72.25 | 294.13 | 22.10 |
| 75.25 | 299.60 | 22.31 |
| 77.25 | 293.13 | 22.07 |
| 79.25 | 284.67 | 21.75 |
| 80.25 | 256.31 | 20.63 |
| 81.25 | 198.33 | 18.15 |
3. 数据分析。
- 使用表2中的压力差值 (pT -p2确定速度剖面。在表2中输入结果。
- 使用半径将表2中的压力和速度值绘制为横坐标 (
 图 3)。
图 3)。 - 根据表2的速度和半径值计算方程 (8) 中的积分。
- 用方程 (8) 计算各流速的流量系数。
- 使用将放电系数绘制为横坐标.
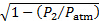
- 对放电系数拟合函数, 幂律是一个很好的选择。

图 3.代表性的结果。(A): 沿流道径向坐标测量静压的例子。(B): 从静压测量中确定的流速分布.请单击此处查看此图的较大版本.
Results
对于在风扇放电时的流量的给定限制,图 3A显示在与托管管进行遍历后, 管道内不同径向位置的动态压力 () 的测量. 这些值用于确定这些径向位置的局部速度, 结果显示在图 3B中。在使用这些数据的梯形规则来求解平均速度的方程 (4) 后, 我们得到了一个 m/s 的值.
这些值用于确定这些径向位置的局部速度, 结果显示在图 3B中。在使用这些数据的梯形规则来求解平均速度的方程 (4) 后, 我们得到了一个 m/s 的值. 另一方面, 表1中的值用于确定公式 (5) 的理想速度: 米/秒. 因此, 此流条件的放电系数为:.
另一方面, 表1中的值用于确定公式 (5) 的理想速度: 米/秒. 因此, 此流条件的放电系数为:. 

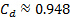 此值在图 4中显示为红色三角形。
此值在图 4中显示为红色三角形。
在重复这个实验二十九次之后, 我们获得了图 4中显示的散点图。的幂定律可以很好地表示此数据: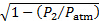
 (11)
(11)
之所以选择这种论点, 是为了确保前导常数保持不变, 因此, 无论压力单位的系统如何, 这种相关性仍然有效。此函数可在公式 (7) 中替代, 以获取流率作为的函数:
 (12)
(12)
在这里, 所有的等式 (7) 和 (11) 的常数被集中到一个单一的无量纲常数:.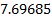 因此, 方程 (12) 对于任何单位的系统都是有效的, 只要变量被一致地分配给相应的单位。为了方便起见, 利用理想气体定律, 从大气压和绝对温度的角度来表达方程 (7) 的密度。方程 (12) 对于不同的大气条件是有效的, 因为它解释了局部压力和温度的变化 (T和Patm)。并且, 只要几何相似性被保守, 这个等式对不同大小的段落是有效的由半径R.
因此, 方程 (12) 对于任何单位的系统都是有效的, 只要变量被一致地分配给相应的单位。为了方便起见, 利用理想气体定律, 从大气压和绝对温度的角度来表达方程 (7) 的密度。方程 (12) 对于不同的大气条件是有效的, 因为它解释了局部压力和温度的变化 (T和Patm)。并且, 只要几何相似性被保守, 这个等式对不同大小的段落是有效的由半径R.
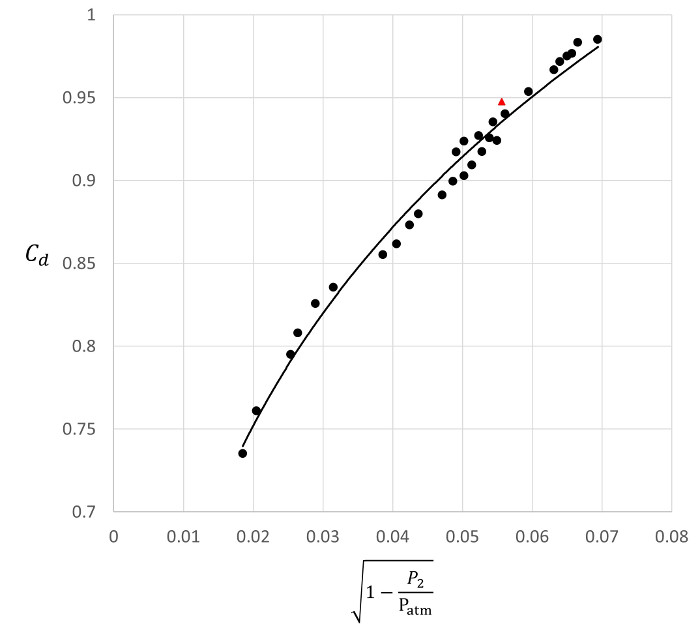
图4。代表结果.: 在不同流速下确定的放电系数.  : 根据此处演示的速度测量确定的放电系数.-: 适用于实验数据的幂定律.
: 根据此处演示的速度测量确定的放电系数.-: 适用于实验数据的幂定律. 
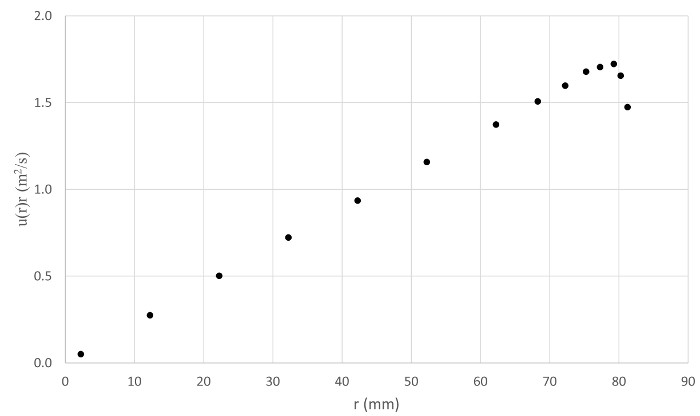
图 6.代表性结果。产品在速度和半径之间的图形.
表3。代表性的结果。放电系数。
| √ (1-p2/patm ) | Cd |
| 0.019 | 0.735 |
| 0.020 | 0.761 |
| 0.025 | 0.795 |
| 0.026 | 0.808 |
| 0.029 | 0.826 |
| 0.032 | 0.835 |
| 0.039 | 0.855 |
| 0.041 | 0.862 |
| 0.042 | 0.873 |
| 0.044 | 0.880 |
| 0.047 | 0.891 |
| 0.049 | 0.899 |
| 0.049 | 0.917 |
| 0.050 | 0.924 |
| 0.050 | 0.903 |
| 0.051 | 0.909 |
| 0.052 | 0.927 |
| 0.053 | 0.917 |
| 0.054 | 0.926 |
| 0.054 | 0.935 |
| 0.055 | 0.924 |
| 0.056 | 0.940 |
| 0.060 | 0.953 |
| 0.063 | 0.967 |
| 0.064 | 0.972 |
| 0.065 | 0.975 |
| 0.066 | 0.977 |
| 0.067 | 0.983 |
| 0.069 | 0.985 |
Application and Summary
我们演示了控制体积分析的应用质量守恒, 以校准流量通道作为流量计。为此, 我们展示了使用一个皮托管系统, 以确定流量通道的流速通过集成的速度剖面。然后, 引入了流量系数的概念, 考虑了边界层生长对流道壁附近的影响。根据一组不同流速的速度测量, 我们开发了一种回归, 它将流量系数表示为流道静压与局部大气压比值的函数,. 最后, 这种回归被合并成一个等式为流动率通过段落作为一个函数.
最后, 这种回归被合并成一个等式为流动率通过段落作为一个函数. 该方程的发展, 以保持其有效性的变化, 在当地大气条件, 通道大小, 和单位系统。
该方程的发展, 以保持其有效性的变化, 在当地大气条件, 通道大小, 和单位系统。
控制容积分析为大规模保护提供了许多选择, 以校准流量通道作为流量计。例如, 穿孔板、喷嘴和文丘里管在密闭流中使用, 以根据通道的两个不同部分的压力变化来确定流速。与我们的例子相似, 这些器件需要具有一个能校正边界层效应的放电系数。
在通过明渠流动时, 质量守恒的控制容积分析也可以通过比较流量限制 (如溢洪道、部分打开的闸门或截面的减少) 前后的流量的深度来评估流量。这些应用的主要意义是, 水的分配, 控制和处理的水力结构是非常大的规模, 将排除其他流动装置的使用。
Tags
跳至...
此集合中的视频:

Now Playing
质量守恒和流速测量
Mechanical Engineering
22.9K Views

浮力和拖曳在浸没的身体
Mechanical Engineering
30.2K Views

浮动容器的稳定性
Mechanical Engineering
22.9K Views

推进力和推力
Mechanical Engineering
22.0K Views

管道网络和压力损失
Mechanical Engineering
58.7K Views

淬火和沸腾
Mechanical Engineering
8.1K Views

液压跳跃
Mechanical Engineering
41.3K Views

换热器分析
Mechanical Engineering
28.3K Views

制冷概论
Mechanical Engineering
24.9K Views

热丝测速
Mechanical Engineering
15.8K Views

测量紊流
Mechanical Engineering
13.6K Views

通过钝体流的可视化
Mechanical Engineering
12.1K Views

射流撞击斜面板
Mechanical Engineering
10.8K Views

系统分析中的能量守恒方法
Mechanical Engineering
7.4K Views

用控制容积法测定扁板的撞击力
Mechanical Engineering
26.0K Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。