Détermination des forces d'impact sur une surface plane via la méthode des volumes de contrôle
Vue d'ensemble
Source : Ricardo Mejia-Alvarez et Hussam Hikmat Jabbar, département de génie mécanique, Michigan State University, East Lansing, MI
Le but de cette expérience est de démontrer la force sur les corps à la suite de changements dans la dynamique linéaire de l’écoulement autour d’eux à l’aide d’une formulation de volume control [1, 2]. L’analyse du volume de contrôle met l’accent sur l’effet macroscopique du courant sur l’ingénierie des systèmes, plutôt que la description détaillée qui pourrait être obtenue avec une analyse différentielle. Chacun de ces deux techniques ont une place dans la boîte à outils d’un analyste technique, et elles devraient être considérées comme complémentaires plutôt que concurrents des approches. Grosso modo, l’analyse du volume contrôle donnera l’ingénieur une idée des charges dominantes dans un système. Cela donnera à cette personne un sentiment initial sur quel itinéraire pour poursuivre lors de la conception de dispositifs ou structures et devrait idéalement être la première étape à prendre avant de poursuivre toute conception détaillée ou analyse par formulation différentielle.
Le principe derrière la formulation de volume de contrôle est de remplacer les détails d’un système exposé à un écoulement de fluide par un diagramme de corps libre simplifié défini par un imaginaire fermé surface doublé le volume de contrôle. Ce diagramme doit contenir toutes les forces de surface et le corps, le flux net du moment linéaire à travers les limites du volume control et le taux de variation du moment linéaire à l’intérieur du volume de contrôle. Cette approche implique habilement définir le volume de contrôle de manière à simplifier l’analyse en même temps qui captent les dominantes effets sur le système. Cette technique sera en démonstration au jet avion empiétant sur une plaque plane à différents angles. Nous utiliserons l’analyse contrôle volume pour estimer la charge aérodynamique sur la plaque et comparer nos résultats avec des mesures réelles de la force résultante obtenue avec un équilibre aérodynamique.
Principles
Un volume de contrôle (CV) est défini par une surface fermée imaginaire, surnommée la surface de contrôle (CS), définie arbitrairement pour étudier l’effet de l’écoulement autour des objets et des systèmes. La figure 1 montre un exemple d’un volume de contrôle contenant une zone d’écoulement allant autour d’un objet solid. L’écoulement dans le voisinage immédiat de l’objet est très complexe, et nous tenons à éviter cette complexité afin d’estimer l’effet global de l’écoulement sur l’élément porteur. Une fois défini, le CV devient un diagramme du corps libre qui capture les interactions entre le flux et l’objet clos qui donnent lieu à des charges dans le système de prise en charge. À cette fin, nous assimilons la surface et des forces de corps sur le CV avec le changement du moment linéaire du flux qui traverse le CV. Les forces de surface sont la pression induite par le flux de cisaillement et des réactions des solides « coupés » par le volume de contrôle. Les forces du corps sont essentiellement le poids de tout le contenu dans le volume de contrôle, y compris les matières solides et liquides et toute autre force induite par les effets volumétriques tels que les champs électromagnétiques. Le changement dans l’élan linéaire du flux est l’effet du flux net d’impulsion par le CS et le taux de variation du moment figurant dans le CV. Tous ces effets peuvent se résumer dans l’équation de conservation du moment linéaire en forme intégrale :
 (1)
(1)
Ici,  sont les forces de surface et
sont les forces de surface et  sont les forces du corps. Le premier terme à droite de l’équation (1) représente le taux de variation de quantité de mouvement à l’intérieur du volume de contrôle, tandis que le second terme représente le flux net d’élan à travers la surface de contrôle. La différence de vecteur
sont les forces du corps. Le premier terme à droite de l’équation (1) représente le taux de variation de quantité de mouvement à l’intérieur du volume de contrôle, tandis que le second terme représente le flux net d’élan à travers la surface de contrôle. La différence de vecteur  est la vitesse relative entre le CV et le flux et le vecteur
est la vitesse relative entre le CV et le flux et le vecteur  est l’unité vers l’extérieur normaux à la superficie différentielle. Le produit scalaire entre la vitesse relative et
est l’unité vers l’extérieur normaux à la superficie différentielle. Le produit scalaire entre la vitesse relative et  représente la composante de vitesse qui traverse le CS et désormais contribue à l’échange du moment linéaire. Le signe de ce produit scalaire est négatif lorsque le flux de quantité de mouvement est dirigé dans le CV et positif où il est dirigé loin de la CV. Sous cette forme, l’équation (1) est l’équilibre du moment linéaire par rapport à un référentiel galiléen de référence. Notez que (1) est une équation vectorielle, qui veut dire qu’en général est a trois composantes indépendantes. Dans cette optique, l’analyste doit faire attention à mettre en place l’ensemble des forces que la balance change dans l’élan linéaire pour chaque coordonnée.
représente la composante de vitesse qui traverse le CS et désormais contribue à l’échange du moment linéaire. Le signe de ce produit scalaire est négatif lorsque le flux de quantité de mouvement est dirigé dans le CV et positif où il est dirigé loin de la CV. Sous cette forme, l’équation (1) est l’équilibre du moment linéaire par rapport à un référentiel galiléen de référence. Notez que (1) est une équation vectorielle, qui veut dire qu’en général est a trois composantes indépendantes. Dans cette optique, l’analyste doit faire attention à mettre en place l’ensemble des forces que la balance change dans l’élan linéaire pour chaque coordonnée.
Pour la démonstration actuelle, nous avons la configuration illustrée dans la Figure 1, où un CV fixe renferme une plaque qui est exposée à un jet de l’avion. Étant donné que le débit du jet est stable, il n’y a aucun changement de quantité de mouvement à l’intérieur de la CV, donc le premier terme à droite de l’équation (1) disparaît. En outre, le CV ne bouge pas, alors  . Par conséquent, la somme des forces exercées sur le CV soldes avec le flux net d’impulsion par le CS.
. Par conséquent, la somme des forces exercées sur le CV soldes avec le flux net d’impulsion par le CS.
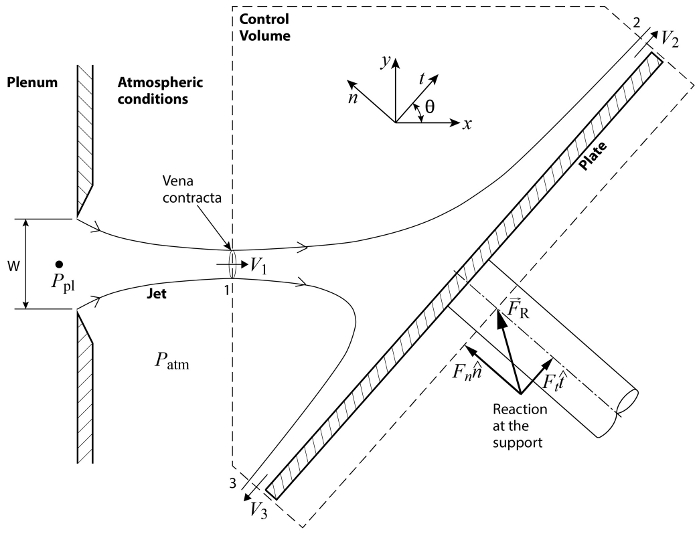
Figure 1 . Schéma de configuration de base. Un jet avion quitte la chambre de tranquillisation à travers une fente de largeur W. Le jet empiète sur une plaque inclinée et il obtient a dévié tout en exerçant une charge sur la surface.
Compte tenu de la configuration de la Figure 1, élan se jette dans le CV à travers port 1 et laisse le CV via les ports 2 et 3. Le CV traverse le jet entrant vers la vena contracta, (pour plus d’informations, s’il vous plaît voir la vidéo « l’interaction entre pression et vitesse : jet empiétant sur une plaque inclinée ») qui est le premier endroit où les lignes de courant deviennent parallèle et, en conséquence, la pression statique dans le jet devient homogène et correspond à la valeur de la pression environnante, autrement dit, la pression atmosphérique  . De même, les ports 2 et 3 sont situés assez loin de la région incidente pour permettre de devenir parallèle et la pression des lignes doit correspondre à celui des environs. Par conséquent, la pression partout sur le CS est égale à la pression atmosphérique,
. De même, les ports 2 et 3 sont situés assez loin de la région incidente pour permettre de devenir parallèle et la pression des lignes doit correspondre à celui des environs. Par conséquent, la pression partout sur le CS est égale à la pression atmosphérique,  . En conséquence, étant donné que la pression est distribuée de façon homogène autour de la CS, sa force nette sur le volume de contrôle est nulle. En outre, étant donné que le CS a été dessiné perpendiculairement au flux d’entrée et de sortie, il n’est pas n’importe quelle charge de cisaillement induite par la circulation sur le CS. En résumé, l’équation (1) simplifie la relation suivante pour le cas illustré à la Figure 1
. En conséquence, étant donné que la pression est distribuée de façon homogène autour de la CS, sa force nette sur le volume de contrôle est nulle. En outre, étant donné que le CS a été dessiné perpendiculairement au flux d’entrée et de sortie, il n’est pas n’importe quelle charge de cisaillement induite par la circulation sur le CS. En résumé, l’équation (1) simplifie la relation suivante pour le cas illustré à la Figure 1
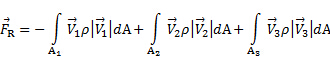 (2)
(2)
Ici,  est la réaction du support système résultant de la transmission de la charge aérodynamique que le jet exerce sur la plaque. Comme illustré à la Figure 1, cette réaction est située à la partie du volume control qui « traverse », le système de support de la plaque. Ceci est considéré comme une force de surface en ce sens que cet imaginaire coupe ferait partie de la surface de contrôle. Étant donné que
est la réaction du support système résultant de la transmission de la charge aérodynamique que le jet exerce sur la plaque. Comme illustré à la Figure 1, cette réaction est située à la partie du volume control qui « traverse », le système de support de la plaque. Ceci est considéré comme une force de surface en ce sens que cet imaginaire coupe ferait partie de la surface de contrôle. Étant donné que  est la seule interaction avec le volume de contrôle non associé le flux de quantité de mouvement, c’est le seul terme sur le côté gauche des équations (1) et (2). Note de la comparaison de ces équations entre eux les produits scalaires dans les intégrales d’entraîner simplement les amplitudes des vecteurs vitesse correspondante parce qu’ils sont alignés avec les vecteurs de l’espace. En outre, comme dit précédemment, leur signe indique si le flux de quantité de mouvement est orienté dans le CV (-) ou loin de lui (+). Si nous supposons de plus que la vitesse dans les ports est approximativement homogène, et que l’écoulement est incompressible, les vitesses et la densité peuvent être prises à l’extérieur les intégrales et l’équation (2) devient :
est la seule interaction avec le volume de contrôle non associé le flux de quantité de mouvement, c’est le seul terme sur le côté gauche des équations (1) et (2). Note de la comparaison de ces équations entre eux les produits scalaires dans les intégrales d’entraîner simplement les amplitudes des vecteurs vitesse correspondante parce qu’ils sont alignés avec les vecteurs de l’espace. En outre, comme dit précédemment, leur signe indique si le flux de quantité de mouvement est orienté dans le CV (-) ou loin de lui (+). Si nous supposons de plus que la vitesse dans les ports est approximativement homogène, et que l’écoulement est incompressible, les vitesses et la densité peuvent être prises à l’extérieur les intégrales et l’équation (2) devient :
 (3)
(3)
Rigoureusement parlant, le profil de vitesse n’est jamais parfaitement homogène, et cette simplification requiert une multiplication par un coefficient de correction,  , dont la valeur dépend des détails de profil de la vitesse. Dans un port donné de flux, ce coefficient est défini comme le rapport entre le flux de l’ampleur exacte et le flux de quantité de mouvement estimée à partir de la vitesse moyenne :
, dont la valeur dépend des détails de profil de la vitesse. Dans un port donné de flux, ce coefficient est défini comme le rapport entre le flux de l’ampleur exacte et le flux de quantité de mouvement estimée à partir de la vitesse moyenne :
 (4)
(4)
Dans les écoulements turbulents, ce coefficient est très proche de 1 car le profil de vitesse a tendance à être proche homogène. Puisque c’est le cas pour la présente expérience, l’équation (3) est une approximation raisonnable pour les mesures. Mais si le débit devait être réduit ou la position de la plaque déplacée plus en aval jusqu'à arriver à des conditions d’écoulement laminaire, il serait nécessaire de résoudre les intégrales sur le côté droit de l’équation (2) sans approximation. Basé sur la Figure 1,  peut être décomposée en ses coordonnées normales et tangentes à la plaque de
peut être décomposée en ses coordonnées normales et tangentes à la plaque de  . Où
. Où 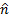 et
et  sont les vecteurs d’unité dans chaque coordonnée et
sont les vecteurs d’unité dans chaque coordonnée et 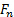 et
et 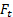 sont les amplitudes des projections des
sont les amplitudes des projections des  dans chaque coordonnée. Donc, l’équation (3) peut être décomposée comme :
dans chaque coordonnée. Donc, l’équation (3) peut être décomposée comme :
 (5)
(5)
Remarque que le signe moins sur la composante normale disparaît car la projection de  sur l’axe normal est négatif. Nous voulons déterminer la charge normale sur la plaque avec cette étude parce qu’elle tend à être plus au niveau du composant du point de vue structurel. L’équation (4), on obtient la charge normale sur la plaque :
sur l’axe normal est négatif. Nous voulons déterminer la charge normale sur la plaque avec cette étude parce qu’elle tend à être plus au niveau du composant du point de vue structurel. L’équation (4), on obtient la charge normale sur la plaque :
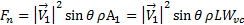 (6)
(6)
Ici, 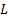 est la durée de la plaque et
est la durée de la plaque et 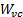 est la largeur du jet à la vena contracta. En général, le taux de contraction entre le jet sortir largeur,
est la largeur du jet à la vena contracta. En général, le taux de contraction entre le jet sortir largeur,  , et la vena contracta est très proche [2, 3, 4] :
, et la vena contracta est très proche [2, 3, 4] :
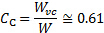 (7)
(7)
En résumé, la force normale sur la plaque peut être estimée par la relation suivante :
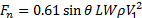 (8)
(8)
Nous définissons ici,  pour plus de simplicité. D’autre part, la valeur de l’expression
pour plus de simplicité. D’autre part, la valeur de l’expression  est déterminé en utilisant l’équation de Bernoulli entre le plenum et le vena contracta (voir la Figure 2 pour référence). La vitesse à l’intérieur de l’Assemblée plénière est considéré comme négligeable, et étant donné que le jet est horizontal, les changements de hauteur entre le plenum et le vena contracta disparaissent. Équation de Bernoulli devient donc :
est déterminé en utilisant l’équation de Bernoulli entre le plenum et le vena contracta (voir la Figure 2 pour référence). La vitesse à l’intérieur de l’Assemblée plénière est considéré comme négligeable, et étant donné que le jet est horizontal, les changements de hauteur entre le plenum et le vena contracta disparaissent. Équation de Bernoulli devient donc :
 (9)
(9)
Rappelons que la pression à la vena contracta correspond à la pression environnante, ce qui est atmosphérique. Par conséquent, la pression dynamique à la vena contracta suit :
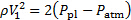 (10)
(10)
Son remplacement par l’équation (9) dans l’équation (7) donne le résultat final pour estimer la force normale sur la plaque selon les caractéristiques du jet avion :
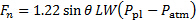 (11)
(11)
Ce résultat provient de l’analyse de volume de contrôle de la conservation du moment linéaire. Pour avoir une évaluation de l’exactitude des informations, Nous comparerons ces estimations pour ordonner des mesures de la force. À cette fin, l’horizontale (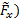 et verticaux (
et verticaux ( constitutifs de la force totale illustrée au tableau 2 sont capturés par un équilibre aérodynamique. Pour déterminer les composants de ce mesure force sur les
constitutifs de la force totale illustrée au tableau 2 sont capturés par un équilibre aérodynamique. Pour déterminer les composants de ce mesure force sur les  système de coordonnées, nous utilisons la transformation des coordonnées suivante :
système de coordonnées, nous utilisons la transformation des coordonnées suivante :
 (12)
(12)
 (13)
(13)
Où un tilde a été ajouté pour souligner que ces forces sont obtenues par mesure directe avec un équilibre aérodynamique.
Procédure
1. réglage de l’installation
- Assurez-vous qu’il n’y a pas de débit dans l’installation.
- Connectez le port positif du transducteur de pression au robinet de pression de plénum (
 ).
). - Laissez le port négatif du transducteur de pression ouverte dans l’atmosphère (
 ).
). - Enregistrer le facteur de conversion du transducteur de Volts en Pascals (
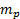 ).
). - Enregistrer la largeur de sortie du jet.
- Enregistrer la durée de la plaque.
- Enregistrer les constantes de conversion de l’équilibre des forces entre Volts à Newton (force horizontale :
 ; vertical force :
; vertical force :  ).
). - Configurer le système d’acquisition de données de l’échantillon à une fréquence de 100 Hz pour un total de 1000 échantillons (c'est-à-dire 10 s de données).
- Monter la plaque d’impact sur l’équilibre des forces et ajuster ses sorties à zéro.
2. enregistrement des données
- Régler l’angle de la plaque à 90o (pour référence, voir Figure 2 ).
- Allumez la facilité de circulation.
- Enregistrez la lecture du transducteur de pression en Volts, ce qui correspond à la différence de pression entre l’atmosphère et le plénum (
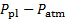 ).
). - Enregistrer les données de force en utilisant le système d’acquisition de données.
- Multiplier les valeurs acquises (en Volts) par les facteurs de conversion de force (
 et
et  ) et entrer les résultats dans le tableau 1.
) et entrer les résultats dans le tableau 1. - Désactiver l’installation des flux.
- Changer l’angle de la plaque.
- Répétez les étapes 2,2 à 2,6 pour les angles suivants :
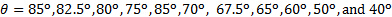

Figure 2. Paramètre expérimental. (A) : détail du système d’admission pour pressuriser le plénum à pression  . (B) : côté avec plaque impingement refoulement. (C) : détail de la fente de la décharge. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.
. (B) : côté avec plaque impingement refoulement. (C) : détail de la fente de la décharge. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.
3. analyse des données
- Calculer la force normale mesurée par le solde à l’aide de equation(11) et les consigner dans le tableau 1.
- Déterminer la valeur théorique de la force normale de l’équation (10) et les consigner dans le tableau 1.
- Calculer le désaccord entre les deux valeurs en pourcentage.
Le tableau 1. Paramètres de base pour l’étude expérimentale.
| Paramètre | Valeur |
| Largeur de bec de jet (W) | pas de 19,05 mm |
| Durée de la plaque (L) | 110,49 cm |
| Constante d’étalonnage de capteur (m_p) | 141.3829 Pa/V |
| Coefficient d’équilibre horizontal (m_x) | 22.2411 N/V |
| Coefficient d’équilibre vertical (m_y) | 4.4482 N/V |
Résultats
La figure 3 montre une comparaison entre la charge normale sur l’assiette plate mesuré directement à partir de l’équilibre aérodynamique et estimée de la conservation du moment linéaire. En général, l’analyse du moment linéaire capturé la tendance dominante des mesures directes comme les changements d’angle impingement. Les divergences dans ces mesures varient non monotone avec l’angle d’incidence. Pour les angles d’impaction dans la gamme 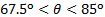 et pour
et pour  , écarts sont inférieurs à 6 %. Ils sont plus élevés pour les autres angles, mais jamais supérieure à 12,5 %. Il semble exister un crossover autour de
, écarts sont inférieurs à 6 %. Ils sont plus élevés pour les autres angles, mais jamais supérieure à 12,5 %. Il semble exister un crossover autour de 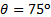 , in qui inversent la tendance des écarts : mesures présentent des charges normales plus élevés que l’analyse du moment linéaire pour
, in qui inversent la tendance des écarts : mesures présentent des charges normales plus élevés que l’analyse du moment linéaire pour  et plus bas pour
et plus bas pour 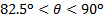 . Ces différences dans les tendances pourraient être due au fait que l’analyse du moment linéaire suppose non visqueux et non dissipatifs, modification de l’impulsion, tandis que des mesures directes ne peuvent éviter l’effet de la viscosité sur le flux. Pour la gamme
. Ces différences dans les tendances pourraient être due au fait que l’analyse du moment linéaire suppose non visqueux et non dissipatifs, modification de l’impulsion, tandis que des mesures directes ne peuvent éviter l’effet de la viscosité sur le flux. Pour la gamme  , la composante de cisaillement devient dominante et donc les effets de la couche limite turbulente pourraient être importants. Dans ce cas, les fluctuations de la vitesse normale mur dû à la turbulence peuvent être responsables de l’augmentation de la charge normale. En revanche, la vitesse axiale du jet subit une réduction significative de la gamme
, la composante de cisaillement devient dominante et donc les effets de la couche limite turbulente pourraient être importants. Dans ce cas, les fluctuations de la vitesse normale mur dû à la turbulence peuvent être responsables de l’augmentation de la charge normale. En revanche, la vitesse axiale du jet subit une réduction significative de la gamme 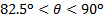 pendant que celui-ci tourne à devenir dominante tangent au mur. Cet effet est susceptible de laisser viscosité viscosité due à une réduction des valeurs locales de nombre de Reynolds de dissiper, et qui se traduirait par des valeurs réduites de la charge normale.
pendant que celui-ci tourne à devenir dominante tangent au mur. Cet effet est susceptible de laisser viscosité viscosité due à une réduction des valeurs locales de nombre de Reynolds de dissiper, et qui se traduirait par des valeurs réduites de la charge normale.
Tableau 2 . Résultats représentatifs.
| Θ | F ̃_x(N) | ̃_y F (N) | ̃_n F (N) | F_n (N) | Ε (%) |
| 90o | 15.257 | 9.034 | 15.257 | 16.773 | 9,9 |
| 85o | 15.151 | 9.831 | 15.950 | 16.709 | 4.8 |
| 82.5o | 15.035 | 10.231 | 16,242 | 16.630 | 2.4 |
| 80o | 15.929 | 10.498 | 17.510 | 16.518 | 5.7 |
| 75o | 14,248 | 10.453 | 16,468 | 16.202 | 1.6 |
| 70o | 13.518 | 11.405 | 16.604 | 15.762 | 5.1 |
| 67,5o | 13.100 | 11.294 | 16.425 | 15.496 | 5.7 |
| 65o | 12.771 | 11.579 | 16,468 | 15.202 | 7.7 |
| 60o | 11.881 | 11.863 | 16.221 | 14.526 | 10.5 |
| 50o | 9.746 | 11.241 | 14.691 | 12.849 | 12,5 |
| 40o | 6.357 | 9.444 | 11.320 | 10.782 | 4.8 |

Figure 3 . Résultats représentatifs. Charge sur la plaque à la suite d’empiétant jet. Les symboles représentent :  : direct de mesure de la charge ;
: direct de mesure de la charge ;  : estimation de la conservation du moment linéaire ;
: estimation de la conservation du moment linéaire ;  : pourcentage d’erreur entre les mesures expérimentales et théorique estimation. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.
: pourcentage d’erreur entre les mesures expérimentales et théorique estimation. S’il vous plaît cliquez ici pour visionner une version agrandie de cette figure.
Applications et Résumé
Nous avons démontré l’application de l’analyse du volume de contrôle de la conservation du moment linéaire pour déterminer les efforts exercés par un jet empiétant sur une plaque plane. Cette analyse s’est avérée simple à appliquer et a donné une estimation satisfaisante en vrac des charges sans nécessiter une connaissance détaillée du modèle d’écoulement autour de la plaque. S’il y avait quelques divergences (à la fois en grandeur mais aussi tendance) en raison de l’hypothèse de base de transformation non visqueux de l’élan, cette technique offre un moyen d’obtenir une estimation rapide du fonctionnement du système sans plonger dans une étude détaillée des écoulement de fluide. Par conséquent, il s’agit d’un outil puissant pour l’analyste technique pour, par exemple, prévoir la possibilité d’élaborer un système donné de génie avec un investissement minimal de temps et de ressources. Une fois cette première analyse est effectuée pour déterminer la faisabilité, l’ingénieur peut se déplacer dans une analyse plus détaillée de flux en utilisant, par exemple, dynamique des fluides computationnelle.
Analyse du volume de contrôle de la conservation du moment linéaire est un outil puissant pour l’ingénierie des fluides. Il trouve application dans une grande variété de problèmes de contourner les impliquer davantage des méthodes telles que l’analyse différentielle. Quelques cas de cette analyse peuvent être décrite :
Design de lame de turbine Pelton : en général, une aube de turbine Pelton devrait être conçue pour convertir le montant le plus élevé du moment linéaire en couple. Ceci est réalisé par la détermination de la géométrie de la lame qui maximise le changement dans l’élan linéaire de jets d’eau. À cette fin, le résultat typique de l’analyse du volume de contrôle est qu’il faudrait le jet pour tourner sur elle-même, c'est-à-dire 180o. C’est en général un défi technique pour un dispositif tournant, mais procure à l’analyste une orientation initiale pour une analyse plus détaillée à l’aide d’autres outils.
Charge d’entraînement sur les structures civiles : un des défis du génie civil est de concevoir des structures qui se dressent à la charge du vent. Afin de prédire les effets du vent sur une structure de taille réelle, il est possible de réaliser des expériences avec un modèle à échelle vers le bas dans les tunnels de vent ou l’eau. À cette fin, il est possible d’utiliser l’analyse du volume de contrôle de la conservation du moment linéaire basée sur les mesures de la vitesse en amont et en aval du modèle pour déterminer la charge apparente sur le prototype. Cette méthode simplifie la campagne expérimentale et permet d’économiser temps, efforts et argent en vue de la construction d’une structure à échelle réelle.
References
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
- Buckingham, E. Note on contraction coefficients of jets of gas. Journal of Research,6:765-775, 1931.
- Lienhard V, J.H. and J.H. Lienhard IV. Velocity coefficients for free jets from sharp-edged orifices. ASME Journal of Fluids Engineering, 106:13-17, 1984.
Passer à...
Vidéos de cette collection:

Now Playing
Détermination des forces d'impact sur une surface plane via la méthode des volumes de contrôle
Mechanical Engineering
26.0K Vues

Flottabilité et traînée sur les corps immergés
Mechanical Engineering
29.9K Vues

Stabilité des vaisseaux flottants
Mechanical Engineering
22.4K Vues

Propulsion et poussée
Mechanical Engineering
21.6K Vues

Réseaux de canalisations et pertes de charge
Mechanical Engineering
58.1K Vues

Refroidissement et ébullition
Mechanical Engineering
7.7K Vues

Ressauts hydrauliques
Mechanical Engineering
40.9K Vues

Analyse des échangeurs de chaleur
Mechanical Engineering
28.0K Vues

Introduction à la réfrigération
Mechanical Engineering
24.7K Vues

Anémomètre à fil chaud
Mechanical Engineering
15.5K Vues

Mesure des écoulements turbulents
Mechanical Engineering
13.5K Vues

Visualisation de l'écoulement après un corps non profilé
Mechanical Engineering
11.8K Vues

Impact d'un jet sur un plan incliné
Mechanical Engineering
10.7K Vues

L'approche de la conservation de l'énergie pour l'analyse des systèmes
Mechanical Engineering
7.4K Vues

Conservation de la masse et mesures de débit
Mechanical Engineering
22.6K Vues