制御体積法による平板の衝突力の測定
概要
ソース: リカルド ・ メヒア アルバレスとコメディフランセーズ Hikmat ジャバー、機械工学科、ミシガン州立大学、イースト ランシング、MI
この実験の目的は、[1, 2] 制御ボリュームの定式化を使用してそれらのまわりの流れの線形運動量の変化の結果として体に力を発揮することです。コントロール ボリュームの解析は差分解析と達成できる詳細な説明よりもむしろ工学システム学の流れの巨視的効果に焦点を当てます。これらの 2 つの方法の各 1 つ、工学アナリストのツールボックスに場所があるし、彼らは競合するアプローチではなく、相補的な見なす必要があります。大まかに言えば、コントロール ボリュームの解析、エンジニアのアイデアを与える支配的な荷重システムで。これは彼女/彼デバイスや構造、デザインを追求するルートし、理想的にべきであるかについて初期感する差動定式化を介して任意の詳細設計や分析を追求する前に取る最初のステップを与えます。
架空のによって定義される簡易自由物体図によって流体の流れにさらされるシステムの詳細を交換する閉鎖コントロール ・ ボリュームと呼ばれる表面制御ボリュームの定式化の背後にある主要な原則からです。この図は、すべての面と体の力、コントロール ボリュームの境界とコントロール ・ ボリューム内の線形運動量の変化率による線形運動量の純フラックスを含める必要があります。このアプローチでは、システム上の支配的な影響をキャプチャ同時分析を簡略化する方法で巧みにコントロール ・ ボリュームを定義するを意味します。この手法は、様々 な角度で平板平面噴流で実証されます。我々 は、板の空力負荷を推定する制御ボリューム解析を使用し、空力バランスで得られた結果の力の実際の測定値の結果を比較します。
原則
制御ボリューム (CV) は、オブジェクトとシステム周りの流れの影響を検討する任意の値に定義制御表面 (CS) と呼ばれる、架空の閉じたサーフェスによって定義されます。図 1 は、ソリッド オブジェクト周りに行く流れの領域を含むコントロール ボリュームの例を示します。オブジェクトのすぐ近くの流れは非常に複雑なおよびサポート要素の流のグローバルな影響を推定するためにその複雑さを回避したいと思います。定義されている CV サポート システムで負荷を生じさせる流れと含まれているオブジェクトの相互作用をキャプチャ自由物体図になります。このため、我々 は表面を同一視して CV CV を通過する流れの線形運動量の変化と力の体。表面の力は、圧力、流体せん断「カット」コントロール ・ ボリュームによって固体の任意の反応を。体の力は、基本的に固体、流体、電磁場など体積効果による他の力など、コントロール ・ ボリュームに含まれているすべての重量です。流れの線形運動量の変化は CS を通して勢いの純のフラックスと履歴書に含まれている運動量の変化率の追加効果。すべてのこれらの効果は、積分形式での線形運動量保存則の式にまとめることができます。
 (1)
(1)
ここでは、 表面の力と
表面の力と 体勢力します。式 (1) の右辺の最初の項はコントロール ボリュームの内部の運動量の変化の割合を表し、2 番目の用語表します制御表面を介して運動量の純フラックス。ベクトルの違い
体勢力します。式 (1) の右辺の最初の項はコントロール ボリュームの内部の運動量の変化の割合を表し、2 番目の用語表します制御表面を介して運動量の純フラックス。ベクトルの違い CV とフロー、およびベクトル間の相対速度は、
CV とフロー、およびベクトル間の相対速度は、 単位を差分領域に外向き法線です。相対速度間の内積と
単位を差分領域に外向き法線です。相対速度間の内積と 線形運動量の交換に CS を交差し、今後貢献する速度成分を表します。この内積の符号が負運動量フラックスが監督には履歴書と正 CV から指示されます。このフォームで式 (1) は参照の慣性フレームに関連して線形運動量のバランスです。(1) はベクトル方程式、つまり一般的には、3 つの独立したコンポーネントには注意してください。これを念頭に、アナリストは、勢力バランスの各座標の線形運動量の変更とのセットを確立することに注意する必要があります。
線形運動量の交換に CS を交差し、今後貢献する速度成分を表します。この内積の符号が負運動量フラックスが監督には履歴書と正 CV から指示されます。このフォームで式 (1) は参照の慣性フレームに関連して線形運動量のバランスです。(1) はベクトル方程式、つまり一般的には、3 つの独立したコンポーネントには注意してください。これを念頭に、アナリストは、勢力バランスの各座標の線形運動量の変更とのセットを確立することに注意する必要があります。
現在のデモでは、固定の CV が平面噴流にさらされているプレートを囲む、図 1 に示すように構成があります。ジェット フローがしっかりしているので、式 (1) の右辺の最初の項が消えるので、CV 内の運動量の変化はありません。また、CV が移動しないので 。それ故に、CV の力の総和は CS を通して勢いの純フラックスでバランスをとります。
。それ故に、CV の力の総和は CS を通して勢いの純フラックスでバランスをとります。
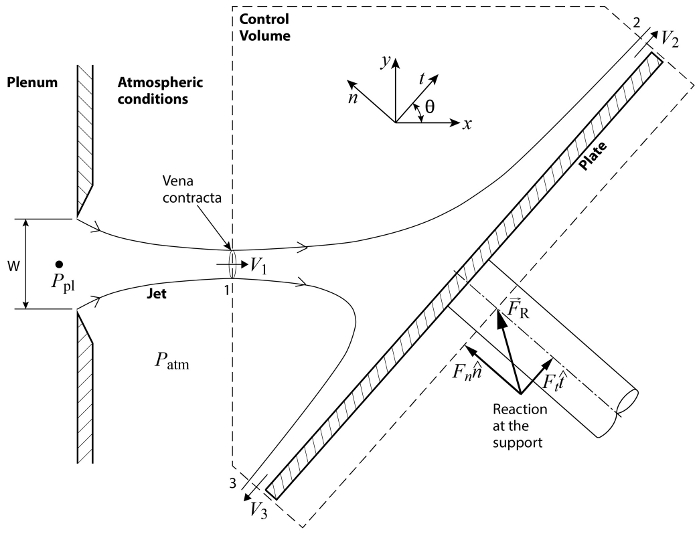
図1.基本的な構成の模式図。平面噴流終了幅のスリットをプレナム W。傾斜平板にジェットが当たるし、それは表面上の負荷を発揮しながら偏向を取得します。
図 1 の構成を考慮した勢いはポート 1 経由 CV に流し込まれ、ポート 2 と 3 によって CV の葉します。CV 十字架に縮み、着信ジェット (詳細については、ビデオを参照してください"の圧力・速度の相互作用: 傾斜平板に衝突する噴流」) 流線が平行し、結果として、なる最初の場所であります。ジェットで静圧が均一になるし、周囲圧は、大気圧の値と一致する 。同様に、ポート 2 と 3 が平行になり、圧力を合理化環境と一致するように衝突領域から十分にずっとあります。その結果、CS のどこでも圧力が大気圧と等しい
。同様に、ポート 2 と 3 が平行になり、圧力を合理化環境と一致するように衝突領域から十分にずっとあります。その結果、CS のどこでも圧力が大気圧と等しい 。その結果、ことを考えると CS の周りの圧力を分散均一制御ボリューム上の正味の力はゼロです。さらに、以来、CS、入口と出口の流れに垂直に描画がない CS の流れによるせん断負荷。要約すると、式 (1) を図 1 に示す事例の次の関係を簡略化します。
。その結果、ことを考えると CS の周りの圧力を分散均一制御ボリューム上の正味の力はゼロです。さらに、以来、CS、入口と出口の流れに垂直に描画がない CS の流れによるせん断負荷。要約すると、式 (1) を図 1 に示す事例の次の関係を簡略化します。
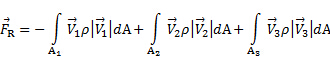 (2)
(2)
ここでは、 ジェットは、プレートに及ぼす空力荷重の伝達から生じるサポート システムの反応です。図 1 に示すとおり、この反応は「カット」プレートのサポート システムを介して制御ボリュームの部分にあります。これは、架空のこのカットという意味で表面力コントロールの表面の一部であると見なされます。以来
ジェットは、プレートに及ぼす空力荷重の伝達から生じるサポート システムの反応です。図 1 に示すとおり、この反応は「カット」プレートのサポート システムを介して制御ボリュームの部分にあります。これは、架空のこのカットという意味で表面力コントロールの表面の一部であると見なされます。以来 だけの相互作用である運動量フラックスに関連付けられていないコントロール ボリューム、それは式 (1) と (2) の左辺の唯一の言葉。これらの方程式、積分内積は、単に対応する速度ベクトルの大きさ面積ベクトルと位置を揃えたのでお互いを比較するから注意してください。また、述べたように、その署名運動量フラックスは CV (-) や (+) それから監督に指示します。我々 はさらに、ポートの速度はおよそ均一と流れは圧縮は、速度と密度を積分の外に取ることができるし、式 (2) になります。
だけの相互作用である運動量フラックスに関連付けられていないコントロール ボリューム、それは式 (1) と (2) の左辺の唯一の言葉。これらの方程式、積分内積は、単に対応する速度ベクトルの大きさ面積ベクトルと位置を揃えたのでお互いを比較するから注意してください。また、述べたように、その署名運動量フラックスは CV (-) や (+) それから監督に指示します。我々 はさらに、ポートの速度はおよそ均一と流れは圧縮は、速度と密度を積分の外に取ることができるし、式 (2) になります。
 (3)
(3)
厳密に言えば、速度分布は完全に均一な決して、この単純化は補正係数で乗算を必要とする 、値が速度プロファイルの詳細によって異なります。与えられたフラックス ポートでこの係数は、正確な運動量フラックスと平均速度から推定された運動量フラックスの比率として定義されます。
、値が速度プロファイルの詳細によって異なります。与えられたフラックス ポートでこの係数は、正確な運動量フラックスと平均速度から推定された運動量フラックスの比率として定義されます。
 (4)
(4)
乱流のこの係数非常に近い 1 速度分布が均一に近い傾向があるので。本実験の場合は、式 (3) は現在の測定のための合理的な近似です。しかし、流量が減少する場合、プレートの位置移動遠く下流層流条件に到達するまで近似せずに式 (2) の右辺の積分を解決する必要があります。図 1 に基づく プレートにその法線および接線座標で分解することができます
プレートにその法線および接線座標で分解することができます 。どこ
。どこ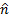 と
と の各座標における単位ベクトルであると
の各座標における単位ベクトルであると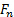 と
と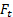 の突起の大きさは、
の突起の大きさは、 各座標で。したがって、式 (3) を分解してすることができます。
各座標で。したがって、式 (3) を分解してすることができます。
 (5)
(5)
通常コンポーネント上のマイナス記号が消えるので、メモの投影 通常軸上が負の値です。我々 は立体構造の観点から最も関連性の高いコンポーネントをする傾向にあるのでこの研究でプレートに通常の負荷を決定します。(4) の式から板に通常の負荷を取得します。
通常軸上が負の値です。我々 は立体構造の観点から最も関連性の高いコンポーネントをする傾向にあるのでこの研究でプレートに通常の負荷を決定します。(4) の式から板に通常の負荷を取得します。
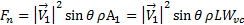 (6)
(6)
ここでは、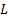 プレート スパンと
プレート スパンと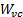 、縮みでジェットの幅です。一般に、収縮比ジェット出口幅、
、縮みでジェットの幅です。一般に、収縮比ジェット出口幅、  、縮みで、非常に近く、[2, 3, 4]。
、縮みで、非常に近く、[2, 3, 4]。
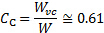 (7)
(7)
要約すると、次の関係からプレートの法線力を推定できます。
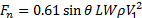 (8)
(8)
ここでは、私たちを定義する わかりやすくするため。その一方で、言葉の値
わかりやすくするため。その一方で、言葉の値 充満および縮み間ベルヌーイの式を使用して決定されます (参照図 2 を参照)。充満の中速度はごくわずかと見なされます、ジェットは水平、充満および縮み間の高さの変化が消えます。それ故に、ベルヌーイの式になります。
充満および縮み間ベルヌーイの式を使用して決定されます (参照図 2 を参照)。充満の中速度はごくわずかと見なされます、ジェットは水平、充満および縮み間の高さの変化が消えます。それ故に、ベルヌーイの式になります。
 (9)
(9)
縮みの圧力が周囲の圧力は、大気中を一致することを思い出してください。それ故、縮みの動的圧力に続きます。
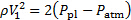 (10)
(10)
平面噴流の特性に基づく平板の法線力を推定する最終的な結果を与える方程式 (9) 式 (7) を置換します。
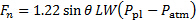 (11)
(11)
この結果は、線形運動量保存則のコントロール ボリュームの分析から来ています。その精度の評価を持っている、我々 は力の直接測定するこれらの推定を比較します。このためには、水平方向 (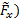 および垂直方向 (
および垂直方向 ( 図 2 に力の合計のコンポーネントは、空力のバランスによってキャプチャされます。このコンポーネントを決定するための力を測定、
図 2 に力の合計のコンポーネントは、空力のバランスによってキャプチャされます。このコンポーネントを決定するための力を測定、 座標系、我々 は次の座標変換を使用して。
座標系、我々 は次の座標変換を使用して。
 (12)
(12)
 (13)
(13)
どこチルダは空力バランスで直接測定によってこれらの力が得られることを強調されました。
手順
1. 施設の設定
- 施設内に流れがないことを確認します。
- チャンバー圧力タップに圧力トランスデューサーの正のポートを接続 (
 )。
)。 - 大気中に圧力トランスデューサーの負のポートを開いたままにしておきます (
 )。
)。 - パスカルにボルトから探触子の変換係数を記録 (
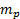 )。
)。 - ジェット出口幅を記録します。
- プレートの範囲を記録します。
- ニュートンにボルトから天秤の変換定数を記録 (水平力:
 ; 垂直力:
; 垂直力:  )。
)。 - 1000 サンプル (すなわち、データの 10 秒) の合計 100 Hz のレートでサンプルにデータ集録システムをセットアップします。
- 力のバランスに影響を与えるプレートをマウントし、ゼロにその出力を調整します。
2. データの記録
- プレートの角度を 90oに設定 (参照図 2を参照)。
- フロー機能をオンにします。
- ボルトは、プレナムと大気との間の圧力の相違に対応する圧力トランスデューサーの読書記録 (
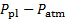 )。
)。 - データ集録システムを使用して力のデータを記録します。
- (ボルト) で取得した値を掛ける力の変換係数 (
 、
、  ) 表 1 に結果を入力。
) 表 1 に結果を入力。 - フロー機能をオフにします。
- プレートの角度を変更します。
- 手順 2.2 に 2.6 を次の角度。

図 2。実験の設定。(A): 圧プレナムを加圧する吸気系の詳細 。(B): 衝突板側を放電します。(C): 放電スリットの詳細。この図の拡大版を表示するのにはここをクリックしてください。
。(B): 衝突板側を放電します。(C): 放電スリットの詳細。この図の拡大版を表示するのにはここをクリックしてください。
3. データ分析
- Equation(11) を使用してバランスを用いて正常な力を計算して表 1 に記録します。
- 関係式 (10) から正常な力の理論値を判断し、表 1 に記録。
- 割合としては、2 つの値の不一致を計算します。
表 1。実験的研究のための基本的なパラメーターです。
| パラメーター | 値 |
| ジェット ノズル幅 (W) | 19.05 mm |
| プレート スパン (L) | 110.49 cm |
| 探触子の校正定数 (m_p) | 141.3829 Pa/V |
| 水平バランス係数 (m_x) | 22.2411 N/V |
| バランス縦係数 (m_y) | 4.4482 N/V |
結果
図 3は、空力バランスから直接測定と線形運動量保存則から推定される平板の通常の負荷の比較を示しています。一般に、線形運動量の分析は、衝突角度の変化として直接測定の支配的な傾向をキャプチャしました。これらの測定の矛盾は非単調衝突角度と様々 な。衝突角度範囲の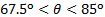 と
と 、不一致が 6% 未満。彼らは他の角より高いが、決して 12.5% よりも高いです。周りのクロス オーバーをするようです
、不一致が 6% 未満。彼らは他の角より高いが、決して 12.5% よりも高いです。周りのクロス オーバーをするようです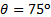 、不一致の傾向を反転する: 測定解析のための線形運動量のより高い通常負荷を示す
、不一致の傾向を反転する: 測定解析のための線形運動量のより高い通常負荷を示す 上下の
上下の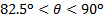 。線形運動量の解析は線形運動量の非粘性, 非散逸の変化を想定して、直接測定は、流れの粘性の影響を避けることはできませんしながらという事実のために、傾向が違う可能性があります。範囲の
。線形運動量の解析は線形運動量の非粘性, 非散逸の変化を想定して、直接測定は、流れの粘性の影響を避けることはできませんしながらという事実のために、傾向が違う可能性があります。範囲の 、せん断成分が支配的になる、したがって乱流境界層の影響が重要であります。この場合、乱流による壁垂直速度変動は通常の負荷の増加の責任があるかもしれない。ジェットの軸流速度が範囲の大幅な削減を経験する一方で
、せん断成分が支配的になる、したがって乱流境界層の影響が重要であります。この場合、乱流による壁垂直速度変動は通常の負荷の増加の責任があるかもしれない。ジェットの軸流速度が範囲の大幅な削減を経験する一方で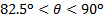 になることになる間支配的壁に接する。この効果はように粘度のレイノルズ数のローカル値の減少による粘度を放散する可能性が、通常の負荷の減少値になるでしょう。
になることになる間支配的壁に接する。この効果はように粘度のレイノルズ数のローカル値の減少による粘度を放散する可能性が、通常の負荷の減少値になるでしょう。
テーブル2.代表の結果。
| Θ | F ̃_x(N) | F ̃_y (N) | F ̃_n (N) | F_n (N) | Ε (%) |
| 90o | 15.257 | 9.034 | 15.257 | 16.773 | 9.9 |
| 85o | 15.151 | 9.831 | 15.950 | 16.709 | 4.8 |
| 82.5o | 15.035 | 10.231 | 16.242 | 16.630 | 2.4 |
| 80o | 15.929 | 10.498 | 17.510 | 16.518 | 5.7 |
| 75o | 14.248 | 10.453 | 16.468 | 16.202 | 1.6 |
| 70o | 13.518 | 11.405 | 16.604 | 15.762 | 5.1 |
| 67.5o | 13.100 | 11.294 | 16.425 | 15.496 | 5.7 |
| 65o | 12.771 | 11.579 | 16.468 | 15.202 | 7.7 |
| 60o | 11.881 | 11.863 | 16.221 | 14.526 | 10.5 |
| 50o | 9.746 | 11.241 | 14.691 | 12.849 | 12.5 |
| 40o | 6.357 | 9.444 | 11.320 | 10.782 | 4.8 |

図3.代表的な結果。衝突噴流によりプレートの負荷します。シンボルを表す:  : 直接負荷測定;
: 直接負荷測定; : 線形運動量の保存からの推定
: 線形運動量の保存からの推定 : 実測と理論的推定パーセント エラーです。この図の拡大版を表示するのにはここをクリックしてください。
: 実測と理論的推定パーセント エラーです。この図の拡大版を表示するのにはここをクリックしてください。
申請書と概要
平板に衝突する噴流によって力を決定する線形運動量保存則の制御ボリューム解析のアプリケーション デモンストレーションを行った。この分析を適用する、簡単な証明プレートまわりのフロー パターンの詳細な知識がなくても荷重の満足のいく一括評価を与えた。この手法の詳細な研究を掘り下げることがなくシステムの動作の簡単な推定を得る手段を提供しています勢いの非粘性変換の基本的な前提のため (両方の傾向と同様、大きさで) いくつかの相違はあるものの、流体の流れ。したがって、例えば、時間とリソースの最小限の投資で与えられた工学システムの開発の可能性を予測する工学アナリストにとって強力なツールです。可能性を決定するため、最初の分析を実施、エンジニア、例えば、数値流体力学を使用してより詳細な流れ解析に移動できます。
線形運動量保存則のコントロール ボリュームの解析は、流体工学のための強力なツールです。それはさまざまな複雑差分解析等を回避するために問題のアプリケーションを検索します。この分析のいくつかのインスタンスを記述することができます。
ペルトン タービン ブレード設計: 一般、ペルトン タービン翼は直線的運動量の最高額をトルクに変換する設計必要があります。これはウォーター ジェットの線形運動量の変化を最大限にブレードの形状を決定することによって達成されます。このため、コントロール ボリューム分析の典型的な結果は、ジェットが振り向く自体、つまり、180oすべきであります。これは一般に回転デバイスの技術的な挑戦が他のツールを使用してより詳細な解析のための初期指導、アナリストを与えます。
土木構造物のドラッグ負荷: 土木工学の課題の 1 つは風の負荷に立つ構造を設計します。風の実大構造に及ぼす影響を予測するために風や水のトンネルでダウン縮小模型実験を行うことが可能です。このため、上流の速度の測定値に基づいて、下位モデルの線形運動量保存則のコントロール ボリュームの分析を使用してプロトタイプの効果的な負荷を確認することが可能です。このメソッドを実験キャンペーンを簡易化および実大構造物の建設のための準備の時間、努力、お金を節約できます。
スキップ先...
このコレクションのビデオ:

Now Playing
制御体積法による平板の衝突力の測定
Mechanical Engineering
26.0K 閲覧数

浮力と浸漬のボディ ドラッグ
Mechanical Engineering
30.2K 閲覧数

浮動のコートの安定性
Mechanical Engineering
23.2K 閲覧数

推進力と推力
Mechanical Engineering
22.1K 閲覧数

配管ネットワークと圧力損失
Mechanical Engineering
58.8K 閲覧数

焼入れと沸騰
Mechanical Engineering
8.2K 閲覧数

油圧ジャンプ
Mechanical Engineering
41.3K 閲覧数

熱交換器の解析
Mechanical Engineering
28.3K 閲覧数

冷凍入門
Mechanical Engineering
25.0K 閲覧数

熱線
Mechanical Engineering
15.9K 閲覧数

乱流を測定
Mechanical Engineering
13.6K 閲覧数

鈍頭物体まわりの流れの可視化
Mechanical Engineering
12.2K 閲覧数

傾斜平板に衝突する噴流
Mechanical Engineering
10.8K 閲覧数

省エネルギー システムの分析方法
Mechanical Engineering
7.4K 閲覧数

質量保存則と流量率測定
Mechanical Engineering
22.9K 閲覧数
Copyright © 2023 MyJoVE Corporation. All rights reserved